Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 103974 by abdomsup last updated on 18/Jul/20

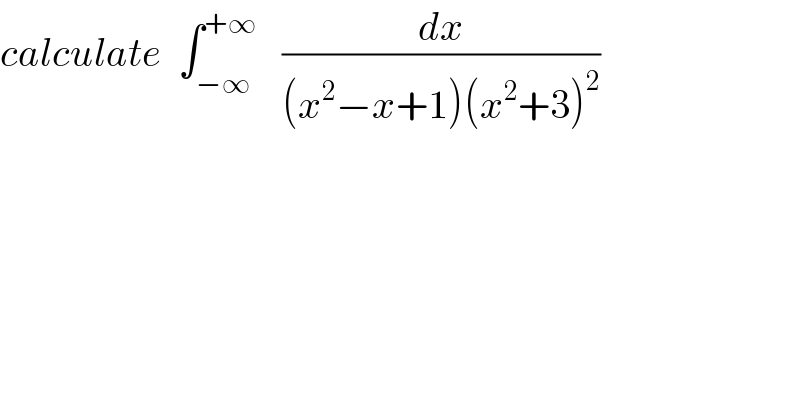
calculate ∫_(−∞) ^(+∞) (dx/((x^2 −x+1)(x^2 +3)^2 ))

$${calculate}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} } \\ $$

Answered by OlafThorendsen last updated on 18/Jul/20

R(x) = (1/((x^2 −x+1)(x^2 +3)^2 )) R(x) = ((x−2)/(7(x^2 +3)^2 ))+((5x−3)/(49(x^2 +3)))−((5x−8)/(x^2 −x+1)) ∫_(−∞) ^(+∞) R(x)dx = −(2/7)∫_(−∞) ^(+∞) (dx/((x^2 +3)^2 )) (I) −(3/(49))∫_(−∞) ^(+∞) (dx/(x^2 +3)) (J) −∫_(−∞) ^(+∞) ((5x−8)/(x^2 −x+1)) (K) (we don′t keep odd functions) I = −(2/7)[(x/(6(x^2 +3)))+(1/(6(√3)))arctan(x/(√3))]_(−∞) ^(+∞) I = −(π/(21(√3))) J = −(3/(49))[(1/(√3))arctan(x/(√3))]_(−∞) ^(+∞) J = −((3π)/(49(√3))) K = −[((11)/(√3))arctan((1/(√3))−((2x)/(√3)))+(5/2)ln(x^2 −x+1)]_(−∞) ^(+∞) K = ((11π)/(√3)) ∫_(−∞) ^(+∞) R(x)dx = I+J+K = −(π/(21(√3)))−((3π)/(49(√3)))+((11π)/(√3)) = ((1601π)/(147(√3))) sorry, i′m not sure of my result.

$$\mathrm{R}\left({x}\right)\:=\:\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\mathrm{R}\left({x}\right)\:=\:\frac{{x}−\mathrm{2}}{\mathrm{7}\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{5}{x}−\mathrm{3}}{\mathrm{49}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{5}{x}−\mathrm{8}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$\int_{−\infty} ^{+\infty} \mathrm{R}\left({x}\right){dx}\:= \\ $$$$−\frac{\mathrm{2}}{\mathrm{7}}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\:\left(\mathrm{I}\right) \\ $$$$−\frac{\mathrm{3}}{\mathrm{49}}\int_{−\infty} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{3}}\:\left(\mathrm{J}\right) \\ $$$$−\int_{−\infty} ^{+\infty} \frac{\mathrm{5}{x}−\mathrm{8}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:\left(\mathrm{K}\right) \\ $$$$\left(\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{keep}\:\mathrm{odd}\:\mathrm{functions}\right) \\ $$$$\mathrm{I}\:=\:−\frac{\mathrm{2}}{\mathrm{7}}\left[\frac{{x}}{\mathrm{6}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}+\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{3}}}\mathrm{arctan}\frac{{x}}{\sqrt{\mathrm{3}}}\right]_{−\infty} ^{+\infty} \\ $$$$\mathrm{I}\:=\:−\frac{\pi}{\mathrm{21}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{J}\:=\:−\frac{\mathrm{3}}{\mathrm{49}}\left[\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\mathrm{arctan}\frac{{x}}{\sqrt{\mathrm{3}}}\right]_{−\infty} ^{+\infty} \\ $$$$\mathrm{J}\:=\:−\frac{\mathrm{3}\pi}{\mathrm{49}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{K}\:=\:−\left[\frac{\mathrm{11}}{\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}−\frac{\mathrm{2}{x}}{\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\right]_{−\infty} ^{+\infty} \\ $$$$\mathrm{K}\:=\:\frac{\mathrm{11}\pi}{\sqrt{\mathrm{3}}} \\ $$$$\int_{−\infty} ^{+\infty} \mathrm{R}\left({x}\right){dx}\:=\:\mathrm{I}+\mathrm{J}+\mathrm{K} \\ $$$$=\:−\frac{\pi}{\mathrm{21}\sqrt{\mathrm{3}}}−\frac{\mathrm{3}\pi}{\mathrm{49}\sqrt{\mathrm{3}}}+\frac{\mathrm{11}\pi}{\sqrt{\mathrm{3}}} \\ $$$$=\:\frac{\mathrm{1601}\pi}{\mathrm{147}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{sorry},\:\mathrm{i}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{of}\:\mathrm{my}\:\mathrm{result}. \\ $$

Commented by mathmax by abdo last updated on 19/Jul/20

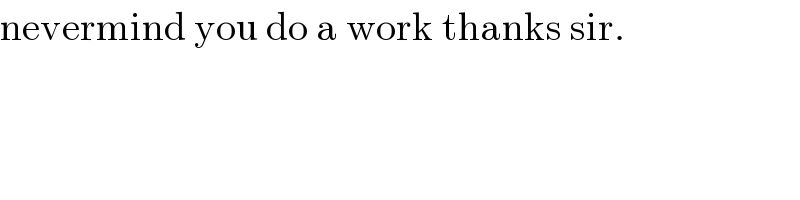
nevermind you do a work thanks sir.

$$\mathrm{nevermind}\:\mathrm{you}\:\mathrm{do}\:\mathrm{a}\:\mathrm{work}\:\mathrm{thanks}\:\mathrm{sir}. \\ $$

Answered by mathmax by abdo last updated on 19/Jul/20

I =∫_(−∞) ^(+∞) (dx/((x^2 −x+1)(x^2 +3)^2 )) let ϕ(z) =(1/((z^2 −z +1)(z^2 +3)^2 )) poles of ϕ z^2 −z+1 =0→Δ =−3 ⇒z_1 =((1+i(√3))/2) =e^((iπ)/3) and z_2 =((1−i(√3))/2) =e^(−((iπ)/3)) ⇒ϕ(z) =(1/((z−e^((iπ)/3) )(z−e^(−((iπ)/3)) )(z−i(√3))^2 (z+i(√3))^2 )) rwsidus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ ,e^((iπ)/3) ) +Res(ϕ,i(√3))} Res(ϕ ,e^((iπ)/3) ) =lim_(z→e^((iπ)/3) ) (z−e^(i(π/3)) )ϕ(z) = (1/(2isin((π/3))(e^((2iπ)/3) +3)^2 )) =(1/(2i((√3)/2)(e^((2iπ)/3) +3)^2 )) Res(ϕ,i(√3)) =lim_(z→i(√3)) (1/((2−1)!)){(z−i(√3))^2 ϕ(z)}^((1)) =lim_(z→i(√3)) {(1/((z^2 −z+1)(z+i(√3))^2 ))}^((1)) =lim_(z→i(√3)) −(((2z−1)(z+i(√3))^2 +2(z+i(√3))(z^2 −z+1))/((z^2 −z+1)^2 (z+i(√3))^4 )) =lim_(z→i(√3)) −(((2z−1)/((z^2 −z+1)^2 (z+i(√3))^2 )) +(2/((z^2 −z+1)(z+i(√3))^3 ))) =−{((2i(√3)−1)/((−3−i(√3)+1)^2 (2i(√3))^2 )) +(2/((−3−i(√3)+1)(2i(√3))^3 ))} =−{((2i(√3)−1)/((2+i(√3))^2 (−12))) +(2/((−2−i(√3))(−24i)))} ....be continued...

$$\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}\:+\mathrm{1}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:\:\mathrm{poles}\:\mathrm{of}\:\varphi \\ $$$$\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\:=\mathrm{0}\rightarrow\Delta\:=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$\Rightarrow\varphi\left(\mathrm{z}\right)\:\:=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}−\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:\:\mathrm{rwsidus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\varphi\:,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:+\mathrm{Res}\left(\varphi,\mathrm{i}\sqrt{\mathrm{3}}\right)\right\} \\ $$$$\mathrm{Res}\left(\varphi\:,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\left(\mathrm{z}−\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} \right)\varphi\left(\mathrm{z}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{2isin}\left(\frac{\pi}{\mathrm{3}}\right)\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\sqrt{\mathrm{3}}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}\sqrt{\mathrm{3}}} \:\:\:\left\{\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}\sqrt{\mathrm{3}}} \:\:\:−\frac{\left(\mathrm{2z}−\mathrm{1}\right)\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}\sqrt{\mathrm{3}}} \:\:\:−\left(\frac{\mathrm{2z}−\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{3}} }\right) \\ $$$$=−\left\{\frac{\mathrm{2i}\sqrt{\mathrm{3}}−\mathrm{1}}{\left(−\mathrm{3}−\mathrm{i}\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\left(−\mathrm{3}−\mathrm{i}\sqrt{\mathrm{3}}+\mathrm{1}\right)\left(\mathrm{2i}\sqrt{\mathrm{3}}\right)^{\mathrm{3}} }\right\} \\ $$$$=−\left\{\frac{\mathrm{2i}\sqrt{\mathrm{3}}−\mathrm{1}}{\left(\mathrm{2}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \left(−\mathrm{12}\right)}\:+\frac{\mathrm{2}}{\left(−\mathrm{2}−\mathrm{i}\sqrt{\mathrm{3}}\right)\left(−\mathrm{24i}\right)}\right\}\:....\mathrm{be}\:\mathrm{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com