
Question Number 10398 by amir last updated on 07/Feb/17

Answered by arge last updated on 07/Feb/17
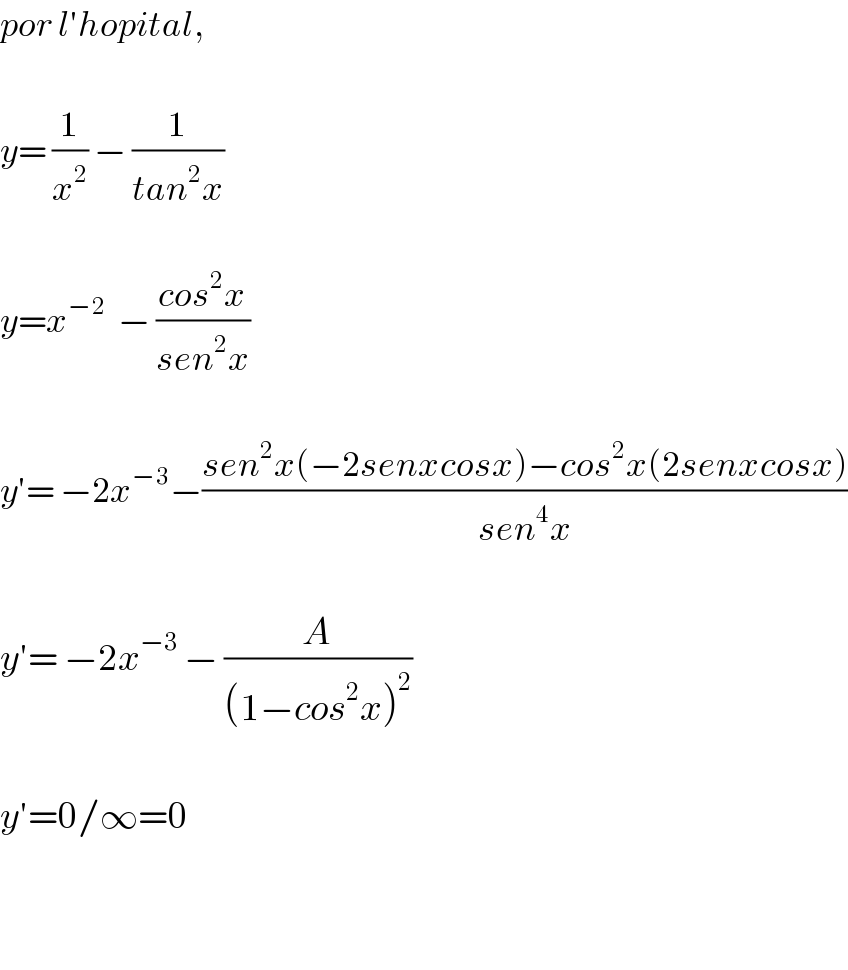
$${por}\:{l}'{hopital}, \\ $$$$ \\ $$$${y}=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{tan}^{\mathrm{2}} {x}} \\ $$$$ \\ $$$${y}={x}^{−\mathrm{2}} \:\:−\:\frac{{cos}^{\mathrm{2}} {x}}{{sen}^{\mathrm{2}} {x}} \\ $$$$ \\ $$$${y}'=\:−\mathrm{2}{x}^{−\mathrm{3}} −\frac{{sen}^{\mathrm{2}} {x}\left(−\mathrm{2}{senxcosx}\right)−{cos}^{\mathrm{2}} {x}\left(\mathrm{2}{senxcosx}\right)}{{sen}^{\mathrm{4}} {x}} \\ $$$$ \\ $$$${y}'=\:−\mathrm{2}{x}^{−\mathrm{3}} \:−\:\frac{{A}}{\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${y}'=\mathrm{0}/\infty=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Answered by mrW1 last updated on 09/Feb/17
![lim_(x→0) ((1/x^2 )−(1/(tan^2 x))) =lim_(x→0) [((1/x)+((cos x)/(sin x)))((1/x)−((cos x)/(sin x)))] =lim_(x→0) [((sin x+xcos x)/(xsin x))×((sin x−xcos x)/(xsin x))] =lim_(x→0) [((sin x+xcos x)/(xsin^2 x))×((sin x−xcos x)/x)] =lim_(x→0) [(((((sin )/x))+cos x)/((((sin x)/x))^2 ))×((sin x−xcos x)/x^3 )] =lim_(x→0) (((((sin )/x))+cos x)/((((sin x)/x))^2 ))×lim_(x→0) ((sin x−xcos x)/x^3 ) =((1+1)/1^2 )×lim_(x→0) ((sin x−xcos x)/x^3 ) =2×lim_(x→0) ((sin x−xcos x)/x^3 ) =2×lim_(x→0) ((cos x−cos x+xsin x)/(3x^2 )) ← applying L′hopital′s rule: lim_(x→c) ((f(x))/(g(x)))=lim_(x→c) ((f′(x))/(g′(x))) =2×lim_(x→0) ((xsin x)/(3x^2 )) =2×lim_(x→0) ((sin x)/(3x)) =(2/3)×lim_(x→0) ((sin x)/x) =(2/3)×1 =(2/3)](Q10452.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:{x}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}\right)\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}\right)\right] \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}{{x}\mathrm{sin}\:{x}}×\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{{x}\mathrm{sin}\:{x}}\right] \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}{{x}\mathrm{sin}^{\mathrm{2}} \:{x}}×\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{{x}}\right] \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\left(\frac{\mathrm{sin}\:}{{x}}\right)+\mathrm{cos}\:{x}}{\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\mathrm{2}} }×\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{{x}^{\mathrm{3}} }\right] \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{sin}\:}{{x}}\right)+\mathrm{cos}\:{x}}{\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\mathrm{2}} }×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{{x}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}+\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{{x}^{\mathrm{3}} } \\ $$$$=\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}−{x}\mathrm{cos}\:{x}}{{x}^{\mathrm{3}} } \\ $$$$=\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{x}−\mathrm{cos}\:{x}+{x}\mathrm{sin}\:{x}}{\mathrm{3}{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\leftarrow\:{applying}\:{L}'{hopital}'{s}\:{rule}:\:\underset{{x}\rightarrow{c}} {\mathrm{lim}}\:\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\underset{{x}\rightarrow{c}} {\mathrm{lim}}\:\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)} \\ $$$$=\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\mathrm{sin}\:{x}}{\mathrm{3}{x}^{\mathrm{2}} }\:\:\:\:\:\: \\ $$$$=\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}}{\mathrm{3}{x}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}}{{x}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{1} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by amir last updated on 09/Feb/17
$${thank}\:{you}\:{dear}\:{mrW}\mathrm{1}. \\ $$
