
Question Number 104028 by mathmax by abdo last updated on 19/Jul/20
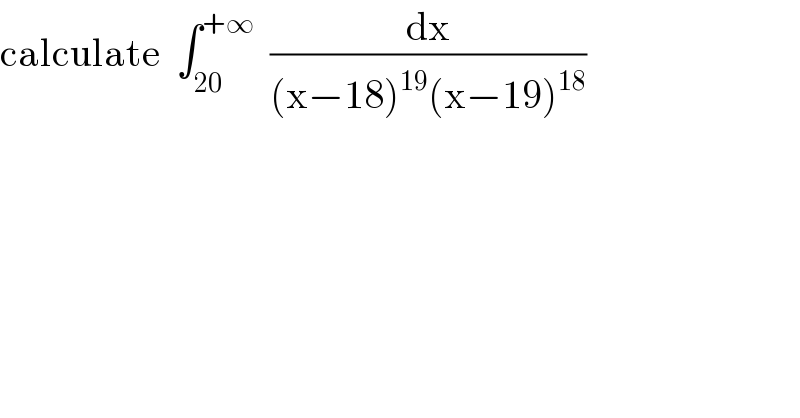
$$\mathrm{calculate}\:\:\int_{\mathrm{20}} ^{+\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{18}\right)^{\mathrm{19}} \left(\mathrm{x}−\mathrm{19}\right)^{\mathrm{18}} } \\ $$
Answered by Dwaipayan Shikari last updated on 19/Jul/20
![∫_(20) ^(+∞) (((x−19)dx)/((x^2 −37x+342)^(19) )) (1/2)∫_(20) ^(+∞) ((2x−37)/((x^2 −37x+342)^(19) ))dx−(1/((x^2 −37+342)^(19) )) −(1/(36))[(1/((x^2 −37x+342)^(18) ))]_(20) ^(+∞) −(1/2)∫(1/((x−18)^(19) (x−19)^(19) )) (1/(36)).(1/2^(18) )−{(1/2)∫_(20) ^(+∞) (1/((x−18)^(19) (x−19)^(19) ))}→I_a (1/(36.2^(18) ))−I_a continue......](Q104080.png)
$$\int_{\mathrm{20}} ^{+\infty} \frac{\left({x}−\mathrm{19}\right){dx}}{\left({x}^{\mathrm{2}} −\mathrm{37}{x}+\mathrm{342}\right)^{\mathrm{19}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{20}} ^{+\infty} \frac{\mathrm{2}{x}−\mathrm{37}}{\left({x}^{\mathrm{2}} −\mathrm{37}{x}+\mathrm{342}\right)^{\mathrm{19}} }{dx}−\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{37}+\mathrm{342}\right)^{\mathrm{19}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{36}}\left[\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{37}{x}+\mathrm{342}\right)^{\mathrm{18}} }\right]_{\mathrm{20}} ^{+\infty} −\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left({x}−\mathrm{18}\right)^{\mathrm{19}} \left({x}−\mathrm{19}\right)^{\mathrm{19}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{36}}.\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{18}} }−\left\{\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{20}} ^{+\infty} \frac{\mathrm{1}}{\left({x}−\mathrm{18}\right)^{\mathrm{19}} \left({x}−\mathrm{19}\right)^{\mathrm{19}} }\right\}\rightarrow{I}_{{a}} \\ $$$$\frac{\mathrm{1}}{\mathrm{36}.\mathrm{2}^{\mathrm{18}} }−{I}_{{a}} \:\:\:\:{continue}...... \\ $$
Answered by mathmax by abdo last updated on 19/Jul/20
![A =∫_(20) ^(+∞) (dx/((x−18)^(19) (x−19)^(18) )) changement x−19 =t give A =∫_1 ^(+∞) (dt/((t+1)^(19) t^(18) )) =∫_1 ^∞ (dt/(((t/(t+1)))^(18) (t+1)^(37) )) we do the changement (t/(t+1)) =u ⇒ t =ut +u ⇒(1−u)t =u ⇒t =(u/(1−u)) ⇒(dt/du) =((1−u+u)/((1−u)^2 )) =(1/((1−u)^2 )) t+1 =(u/(1−u)) +1 =((u+1−u)/(1−u)) =(1/(1−u)) ⇒ A =∫_(1/2) ^1 (du/((1−u)^2 u^(18) ((1/(1−u)))^(37) )) =∫_(1/2) ^1 (((1−u)^(37) )/((1−u)^2 u^(18) ))du =∫_(1/2) ^1 (((1−u)^(35) )/u^(18) ) du =−∫_(1/2) ^1 (((u−1)^(35) )/u^(18) )du =−∫_(1/2) ^1 ((Σ_(k=0) ^(35 ) C_(35) ^k u^k (−1)^(35−k) )/u^(18) )du =Σ_(k=0) ^(35 ) (−1)^k C_(35) ^k ∫_(1/2) ^1 u^(k−18) du =Σ_(k=0 and k≠17) ^(35) (−1)^k C_(35) ^k [(1/(k−17)) u^(k−17) ]_(1/2) ^1 −C_(35) ^(17) [ln∣u∣]_(1/2) ^1 A=Σ_(k=0and k≠17) ^(35) (((−1)^k C_(35) ^k )/(k−17)){1−(1/2^(k−17) )} −ln(2)C_(35) ^(17)](Q104127.png)
$$\mathrm{A}\:=\int_{\mathrm{20}} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{18}\right)^{\mathrm{19}} \left(\mathrm{x}−\mathrm{19}\right)^{\mathrm{18}} }\:\:\mathrm{changement}\:\mathrm{x}−\mathrm{19}\:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dt}}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{19}} \mathrm{t}^{\mathrm{18}} }\:=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dt}}{\left(\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\right)^{\mathrm{18}} \:\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{37}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\:=\mathrm{u}\:\Rightarrow \\ $$$$\mathrm{t}\:=\mathrm{ut}\:+\mathrm{u}\:\Rightarrow\left(\mathrm{1}−\mathrm{u}\right)\mathrm{t}\:=\mathrm{u}\:\Rightarrow\mathrm{t}\:=\frac{\mathrm{u}}{\mathrm{1}−\mathrm{u}}\:\Rightarrow\frac{\mathrm{dt}}{\mathrm{du}}\:=\frac{\mathrm{1}−\mathrm{u}+\mathrm{u}}{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} } \\ $$$$\mathrm{t}+\mathrm{1}\:=\frac{\mathrm{u}}{\mathrm{1}−\mathrm{u}}\:+\mathrm{1}\:=\frac{\mathrm{u}+\mathrm{1}−\mathrm{u}}{\mathrm{1}−\mathrm{u}}\:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{u}}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{du}}{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} \:\mathrm{u}^{\mathrm{18}} \left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{u}}\right)^{\mathrm{37}} }\:\:=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{37}} }{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{2}} \:\mathrm{u}^{\mathrm{18}} }\mathrm{du}\: \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{35}} }{\mathrm{u}^{\mathrm{18}} }\:\mathrm{du}\:=−\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{35}} }{\mathrm{u}^{\mathrm{18}} }\mathrm{du}\:=−\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{35}\:} \:\mathrm{C}_{\mathrm{35}} ^{\mathrm{k}} \:\mathrm{u}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{35}−\mathrm{k}} }{\mathrm{u}^{\mathrm{18}} }\mathrm{du} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{35}\:} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{35}} ^{\mathrm{k}} \:\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\mathrm{u}^{\mathrm{k}−\mathrm{18}} \:\mathrm{du} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{17}} ^{\mathrm{35}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{35}} ^{\mathrm{k}} \:\left[\frac{\mathrm{1}}{\mathrm{k}−\mathrm{17}}\:\mathrm{u}^{\mathrm{k}−\mathrm{17}} \right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\:−\mathrm{C}_{\mathrm{35}} ^{\mathrm{17}} \:\left[\mathrm{ln}\mid\mathrm{u}\mid\right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \\ $$$$\mathrm{A}=\sum_{\mathrm{k}=\mathrm{0and}\:\mathrm{k}\neq\mathrm{17}} ^{\mathrm{35}} \:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{35}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{17}}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{17}} }\right\}\:−\mathrm{ln}\left(\mathrm{2}\right)\mathrm{C}_{\mathrm{35}} ^{\mathrm{17}} \\ $$
