Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 104035 by ajfour last updated on 19/Jul/20

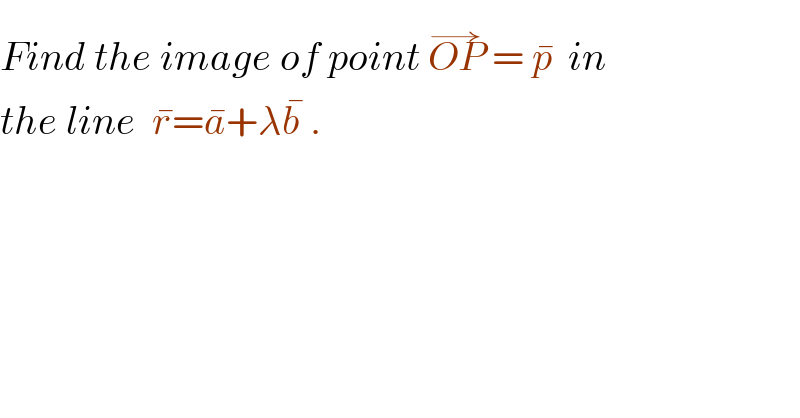
$$Findtheimageofpoint\overrightarrow{OP}=\overline{p}in$$$$theline\overline{r}=\overline{a}+\lambda \overline{b}.$$

Answered by mr W last updated on 19/Jul/20

Commented by mr W last updated on 19/Jul/20

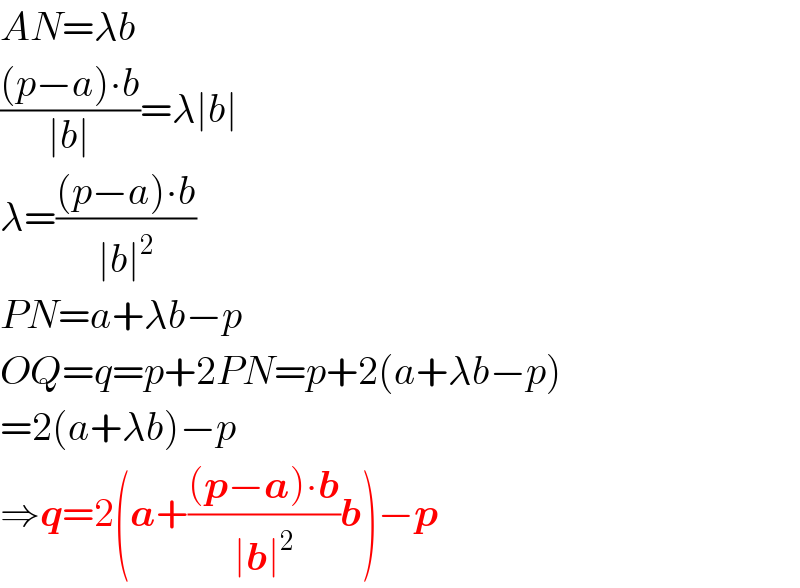
$$AN=\lambda b$$$$\frac{(p-a)\cdot b}{\mid b\mid }=\lambda \mid b\mid$$$$\lambda =\frac{(p-a)\cdot b}{\mid b{\mid }^2}$$$$PN=a+\lambda b-p$$$$OQ=q=p+2PN=p+2(a+\lambda b-p)$$$$=2(a+\lambda b)-p$$$$\Rightarrow \mathit{q}=2(\mathit{a}+\frac{(\mathit{p}-\mathit{a})\cdot \mathit{b}}{\mid \mathit{b}{\mid }^2}\mathit{b})-\mathit{p}$$

Commented by ajfour last updated on 19/Jul/20

$$Ibelieve{this}^{\prime }llbetruefor3Deven$$$$Sir?$$

Commented by mr W last updated on 19/Jul/20

$$basicallyyes.$$

Commented by ajfour last updated on 19/Jul/20

$$\frac{p+q}{2}=a+\lambda b\Rightarrow q=2(a+\lambda b)-p$$$$Now(q-p).b=0$$$$[(a+\lambda b)-p].b=0$$$$\lambda =\frac{(a-p).b}{\mid b{\mid }^2}$$$$\overline{q}=(2\overline{a}-\overline{p})+\left(\frac{2(\overline{a}-\overline{p}).\overline{b}}{\mid \overline{b}{\mid }^2}\right)\overline{b}$$

Commented by mr W last updated on 19/Jul/20

$$yes,thanks!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com