Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104037 by bramlex last updated on 19/Jul/20

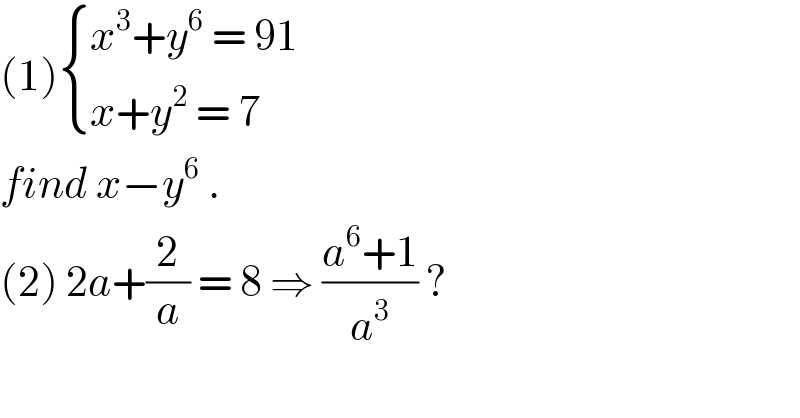
(1) { ((x^3 +y^6 = 91)),((x+y^2 = 7 )) :} find x−y^6 . (2) 2a+(2/a) = 8 ⇒ ((a^6 +1)/a^3 ) ?

$$\left(\mathrm{1}\right)\begin{cases}{{x}^{\mathrm{3}} +{y}^{\mathrm{6}} \:=\:\mathrm{91}}\\{{x}+{y}^{\mathrm{2}} \:=\:\mathrm{7}\:}\end{cases} \\ $$$${find}\:{x}−{y}^{\mathrm{6}} \:. \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2}{a}+\frac{\mathrm{2}}{{a}}\:=\:\mathrm{8}\:\Rightarrow\:\frac{{a}^{\mathrm{6}} +\mathrm{1}}{{a}^{\mathrm{3}} }\:? \\ $$

Answered by bemath last updated on 19/Jul/20

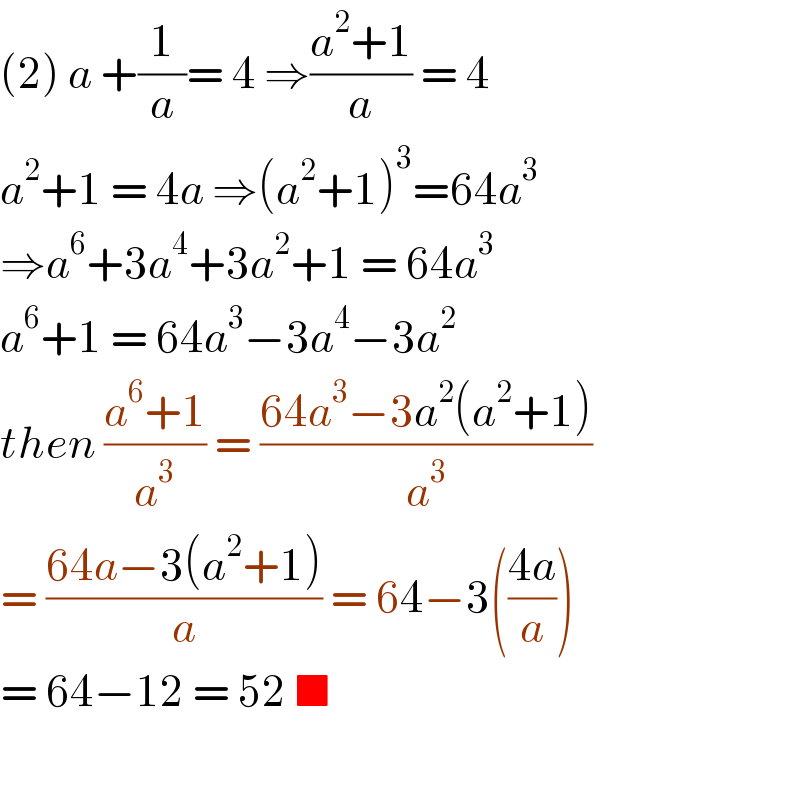
(2) a +(1/a)= 4 ⇒((a^2 +1)/a) = 4 a^2 +1 = 4a ⇒(a^2 +1)^3 =64a^3 ⇒a^6 +3a^4 +3a^2 +1 = 64a^3 a^6 +1 = 64a^3 −3a^4 −3a^2 then ((a^6 +1)/a^3 ) = ((64a^3 −3a^2 (a^2 +1))/a^3 ) = ((64a−3(a^2 +1))/a) = 64−3(((4a)/a)) = 64−12 = 52 ■

$$\left(\mathrm{2}\right)\:{a}\:+\frac{\mathrm{1}}{{a}}=\:\mathrm{4}\:\Rightarrow\frac{{a}^{\mathrm{2}} +\mathrm{1}}{{a}}\:=\:\mathrm{4} \\ $$$${a}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{4}{a}\:\Rightarrow\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} =\mathrm{64}{a}^{\mathrm{3}} \\ $$$$\Rightarrow{a}^{\mathrm{6}} +\mathrm{3}{a}^{\mathrm{4}} +\mathrm{3}{a}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{64}{a}^{\mathrm{3}} \\ $$$${a}^{\mathrm{6}} +\mathrm{1}\:=\:\mathrm{64}{a}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{4}} −\mathrm{3}{a}^{\mathrm{2}} \\ $$$${then}\:\frac{{a}^{\mathrm{6}} +\mathrm{1}}{{a}^{\mathrm{3}} }\:=\:\frac{\mathrm{64}{a}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{1}\right)}{{a}^{\mathrm{3}} } \\ $$$$=\:\frac{\mathrm{64}{a}−\mathrm{3}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}{{a}}\:=\:\mathrm{64}−\mathrm{3}\left(\frac{\mathrm{4}{a}}{{a}}\right) \\ $$$$=\:\mathrm{64}−\mathrm{12}\:=\:\mathrm{52}\:\blacksquare\: \\ $$$$ \\ $$

Answered by bramlex last updated on 19/Jul/20

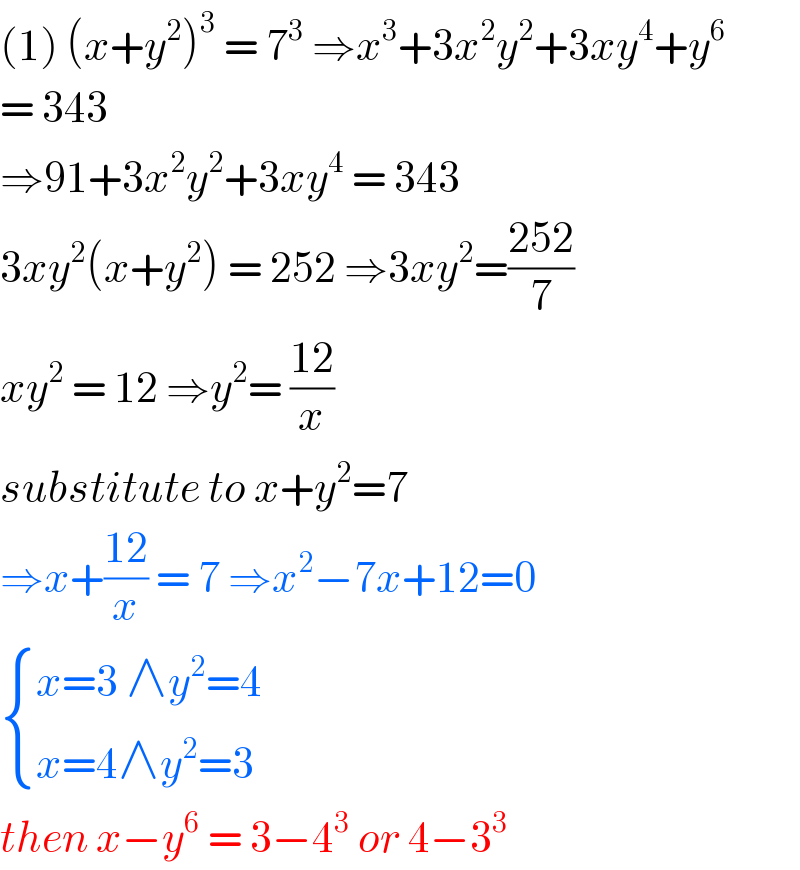
(1) (x+y^2 )^3 = 7^3 ⇒x^3 +3x^2 y^2 +3xy^4 +y^6 = 343 ⇒91+3x^2 y^2 +3xy^4 = 343 3xy^2 (x+y^2 ) = 252 ⇒3xy^2 =((252)/7) xy^2 = 12 ⇒y^2 = ((12)/x) substitute to x+y^2 =7 ⇒x+((12)/x) = 7 ⇒x^2 −7x+12=0 { ((x=3 ∧y^2 =4)),((x=4∧y^2 =3)) :} then x−y^6 = 3−4^3 or 4−3^3

$$\left(\mathrm{1}\right)\:\left({x}+{y}^{\mathrm{2}} \right)^{\mathrm{3}} \:=\:\mathrm{7}^{\mathrm{3}} \:\Rightarrow{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{3}{xy}^{\mathrm{4}} +{y}^{\mathrm{6}} \\ $$$$=\:\mathrm{343}\: \\ $$$$\Rightarrow\mathrm{91}+\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{3}{xy}^{\mathrm{4}} \:=\:\mathrm{343} \\ $$$$\mathrm{3}{xy}^{\mathrm{2}} \left({x}+{y}^{\mathrm{2}} \right)\:=\:\mathrm{252}\:\Rightarrow\mathrm{3}{xy}^{\mathrm{2}} =\frac{\mathrm{252}}{\mathrm{7}} \\ $$$${xy}^{\mathrm{2}} \:=\:\mathrm{12}\:\Rightarrow{y}^{\mathrm{2}} =\:\frac{\mathrm{12}}{{x}} \\ $$$${substitute}\:{to}\:{x}+{y}^{\mathrm{2}} =\mathrm{7} \\ $$$$\Rightarrow{x}+\frac{\mathrm{12}}{{x}}\:=\:\mathrm{7}\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}=\mathrm{0} \\ $$$$\begin{cases}{{x}=\mathrm{3}\:\wedge{y}^{\mathrm{2}} =\mathrm{4}}\\{{x}=\mathrm{4}\wedge{y}^{\mathrm{2}} =\mathrm{3}}\end{cases} \\ $$$${then}\:{x}−{y}^{\mathrm{6}} \:=\:\mathrm{3}−\mathrm{4}^{\mathrm{3}} \:{or}\:\mathrm{4}−\mathrm{3}^{\mathrm{3}} \\ $$

Answered by Dwaipayan Shikari last updated on 19/Jul/20

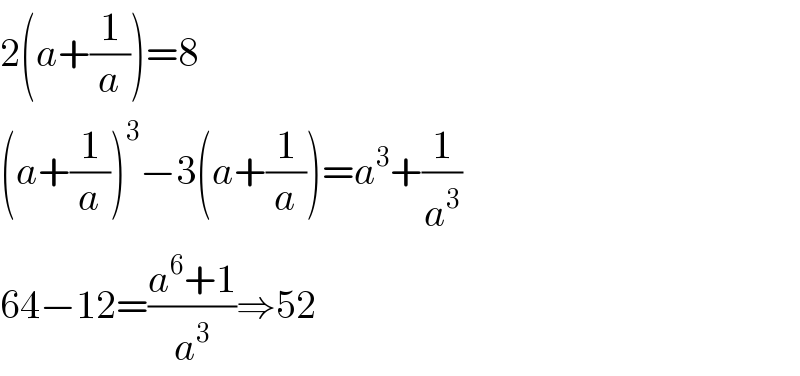
2(a+(1/a))=8 (a+(1/a))^3 −3(a+(1/a))=a^3 +(1/a^3 ) 64−12=((a^6 +1)/a^3 )⇒52

$$\mathrm{2}\left({a}+\frac{\mathrm{1}}{{a}}\right)=\mathrm{8} \\ $$$$\left({a}+\frac{\mathrm{1}}{{a}}\right)^{\mathrm{3}} −\mathrm{3}\left({a}+\frac{\mathrm{1}}{{a}}\right)={a}^{\mathrm{3}} +\frac{\mathrm{1}}{{a}^{\mathrm{3}} } \\ $$$$\mathrm{64}−\mathrm{12}=\frac{{a}^{\mathrm{6}} +\mathrm{1}}{{a}^{\mathrm{3}} }\Rightarrow\mathrm{52} \\ $$

Answered by OlafThorendsen last updated on 19/Jul/20

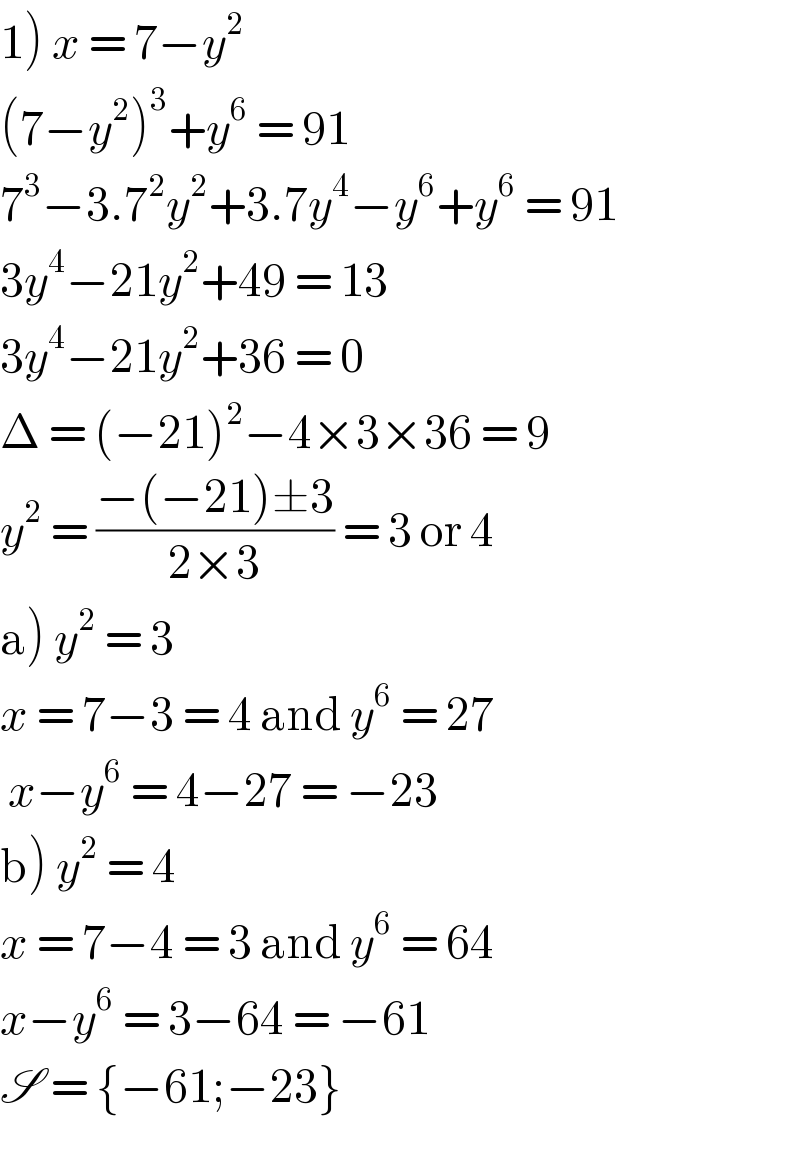
1) x = 7−y^2 (7−y^2 )^3 +y^6 = 91 7^3 −3.7^2 y^2 +3.7y^4 −y^6 +y^6 = 91 3y^4 −21y^2 +49 = 13 3y^4 −21y^2 +36 = 0 Δ = (−21)^2 −4×3×36 = 9 y^2 = ((−(−21)±3)/(2×3)) = 3 or 4 a) y^2 = 3 x = 7−3 = 4 and y^6 = 27 x−y^6 = 4−27 = −23 b) y^2 = 4 x = 7−4 = 3 and y^6 = 64 x−y^6 = 3−64 = −61 S = {−61;−23}

$$\left.\mathrm{1}\right)\:{x}\:=\:\mathrm{7}−{y}^{\mathrm{2}} \\ $$$$\left(\mathrm{7}−{y}^{\mathrm{2}} \right)^{\mathrm{3}} +{y}^{\mathrm{6}} \:=\:\mathrm{91} \\ $$$$\mathrm{7}^{\mathrm{3}} −\mathrm{3}.\mathrm{7}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{3}.\mathrm{7}{y}^{\mathrm{4}} −{y}^{\mathrm{6}} +{y}^{\mathrm{6}} \:=\:\mathrm{91} \\ $$$$\mathrm{3}{y}^{\mathrm{4}} −\mathrm{21}{y}^{\mathrm{2}} +\mathrm{49}\:=\:\mathrm{13} \\ $$$$\mathrm{3}{y}^{\mathrm{4}} −\mathrm{21}{y}^{\mathrm{2}} +\mathrm{36}\:=\:\mathrm{0} \\ $$$$\Delta\:=\:\left(−\mathrm{21}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{3}×\mathrm{36}\:=\:\mathrm{9} \\ $$$${y}^{\mathrm{2}} \:=\:\frac{−\left(−\mathrm{21}\right)\pm\mathrm{3}}{\mathrm{2}×\mathrm{3}}\:=\:\mathrm{3}\:\mathrm{or}\:\mathrm{4} \\ $$$$\left.\mathrm{a}\right)\:{y}^{\mathrm{2}} \:=\:\mathrm{3} \\ $$$${x}\:=\:\mathrm{7}−\mathrm{3}\:=\:\mathrm{4}\:\mathrm{and}\:{y}^{\mathrm{6}} \:=\:\mathrm{27} \\ $$$$\:{x}−{y}^{\mathrm{6}} \:=\:\mathrm{4}−\mathrm{27}\:=\:−\mathrm{23} \\ $$$$\left.\mathrm{b}\right)\:{y}^{\mathrm{2}} \:=\:\mathrm{4} \\ $$$${x}\:=\:\mathrm{7}−\mathrm{4}\:=\:\mathrm{3}\:\mathrm{and}\:{y}^{\mathrm{6}} \:=\:\mathrm{64} \\ $$$${x}−{y}^{\mathrm{6}} \:=\:\mathrm{3}−\mathrm{64}\:=\:−\mathrm{61} \\ $$$$\mathscr{S}\:=\:\left\{−\mathrm{61};−\mathrm{23}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com