Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 104046 by mathocean1 last updated on 19/Jul/20

To do normally his commercial activities in some place situated at 150km from him, a driver use a car. the consumption of gazoil in liters for 10 km is defined by: C(v)=((20)/v)+(v/(45)) where v is the speed of car. How should be the speed of car to reduce minimally the consumption of gazoil?

$$\mathrm{To}\:\mathrm{do}\:\mathrm{normally}\:\mathrm{his}\:\mathrm{commercial} \\ $$$$\mathrm{activities}\:\mathrm{in}\:\mathrm{some}\:\mathrm{place}\:\mathrm{situated}\:\mathrm{at}\:\mathrm{150km} \\ $$$$\mathrm{from}\:\mathrm{him},\:\mathrm{a}\:\mathrm{driver}\:\mathrm{use}\:\mathrm{a}\:\mathrm{car}.\:\mathrm{the}\:\mathrm{consumption} \\ $$$$\mathrm{of}\:\mathrm{gazoil}\:\mathrm{in}\:\mathrm{liters}\:\mathrm{for}\:\mathrm{10}\:\mathrm{km}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{by}: \\ $$$$\mathrm{C}\left(\mathrm{v}\right)=\frac{\mathrm{20}}{\mathrm{v}}+\frac{\mathrm{v}}{\mathrm{45}}\:\mathrm{where}\:\mathrm{v}\:\mathrm{is}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{car}. \\ $$$$\mathrm{How}\:\mathrm{should}\:\mathrm{be}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{car}\:\mathrm{to}\:\mathrm{reduce} \\ $$$$\mathrm{minimally}\:\mathrm{the}\:\mathrm{consumption}\:\mathrm{of}\:\mathrm{gazoil}? \\ $$

Commented by mr W last updated on 19/Jul/20

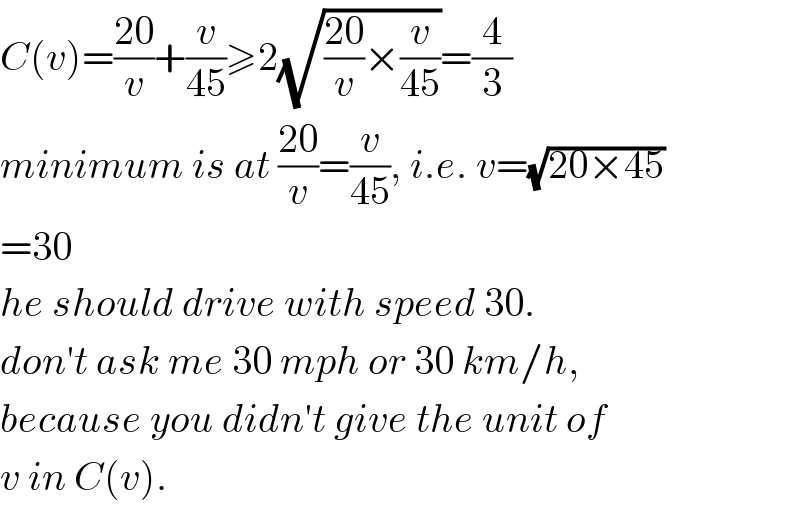
C(v)=((20)/v)+(v/(45))≥2(√(((20)/v)×(v/(45))))=(4/3) minimum is at ((20)/v)=(v/(45)), i.e. v=(√(20×45)) =30 he should drive with speed 30. don′t ask me 30 mph or 30 km/h, because you didn′t give the unit of v in C(v).

$${C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}}\geqslant\mathrm{2}\sqrt{\frac{\mathrm{20}}{{v}}×\frac{{v}}{\mathrm{45}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${minimum}\:{is}\:{at}\:\frac{\mathrm{20}}{{v}}=\frac{{v}}{\mathrm{45}},\:{i}.{e}.\:{v}=\sqrt{\mathrm{20}×\mathrm{45}} \\ $$$$=\mathrm{30} \\ $$$${he}\:{should}\:{drive}\:{with}\:{speed}\:\mathrm{30}. \\ $$$${don}'{t}\:{ask}\:{me}\:\mathrm{30}\:{mph}\:{or}\:\mathrm{30}\:{km}/{h}, \\ $$$${because}\:{you}\:{didn}'{t}\:{give}\:{the}\:{unit}\:{of} \\ $$$${v}\:{in}\:{C}\left({v}\right). \\ $$

Commented by mathocean1 last updated on 19/Jul/20

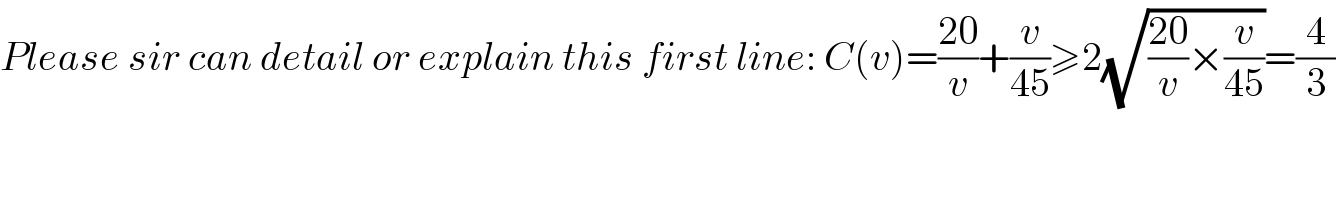
Please sir can detail or explain this first line: C(v)=((20)/v)+(v/(45))≥2(√(((20)/v)×(v/(45))))=(4/3)

$${Please}\:{sir}\:{can}\:{detail}\:{or}\:{explain}\:{this}\:{first}\:{line}:\:{C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}}\geqslant\mathrm{2}\sqrt{\frac{\mathrm{20}}{{v}}×\frac{{v}}{\mathrm{45}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$

Commented by mathocean1 last updated on 19/Jul/20

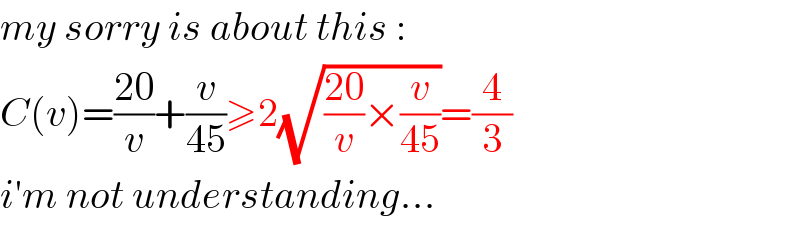
my sorry is about this : C(v)=((20)/v)+(v/(45))≥2(√(((20)/v)×(v/(45))))=(4/3) i′m not understanding...

$${my}\:{sorry}\:{is}\:{about}\:{this}\:: \\ $$$${C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}}\geqslant\mathrm{2}\sqrt{\frac{\mathrm{20}}{{v}}×\frac{{v}}{\mathrm{45}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${i}'{m}\:{not}\:{understanding}... \\ $$

Commented by mr W last updated on 19/Jul/20

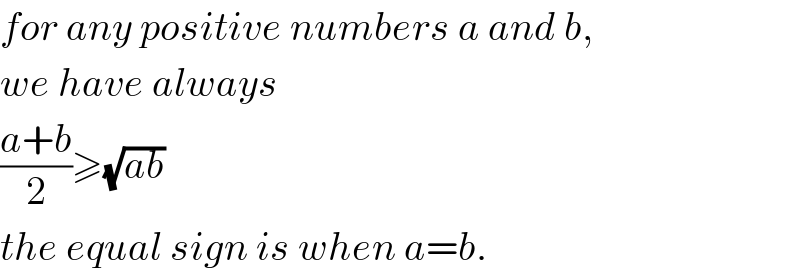
for any positive numbers a and b, we have always ((a+b)/2)≥(√(ab)) the equal sign is when a=b.

$${for}\:{any}\:{positive}\:{numbers}\:{a}\:{and}\:{b}, \\ $$$${we}\:{have}\:{always} \\ $$$$\frac{{a}+{b}}{\mathrm{2}}\geqslant\sqrt{{ab}} \\ $$$${the}\:{equal}\:{sign}\:{is}\:{when}\:{a}={b}. \\ $$

Commented by mr W last updated on 19/Jul/20

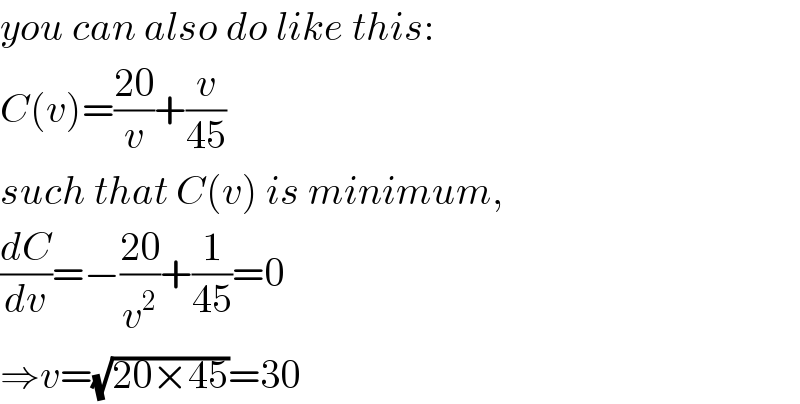
you can also do like this: C(v)=((20)/v)+(v/(45)) such that C(v) is minimum, (dC/dv)=−((20)/v^2 )+(1/(45))=0 ⇒v=(√(20×45))=30

$${you}\:{can}\:{also}\:{do}\:{like}\:{this}: \\ $$$${C}\left({v}\right)=\frac{\mathrm{20}}{{v}}+\frac{{v}}{\mathrm{45}} \\ $$$${such}\:{that}\:{C}\left({v}\right)\:{is}\:{minimum}, \\ $$$$\frac{{dC}}{{dv}}=−\frac{\mathrm{20}}{{v}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{45}}=\mathrm{0} \\ $$$$\Rightarrow{v}=\sqrt{\mathrm{20}×\mathrm{45}}=\mathrm{30} \\ $$

Commented by mathocean1 last updated on 19/Jul/20

thank you very much sir!

$${thank}\:{you}\:{very}\:{much}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com