Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 104051 by bemath last updated on 19/Jul/20

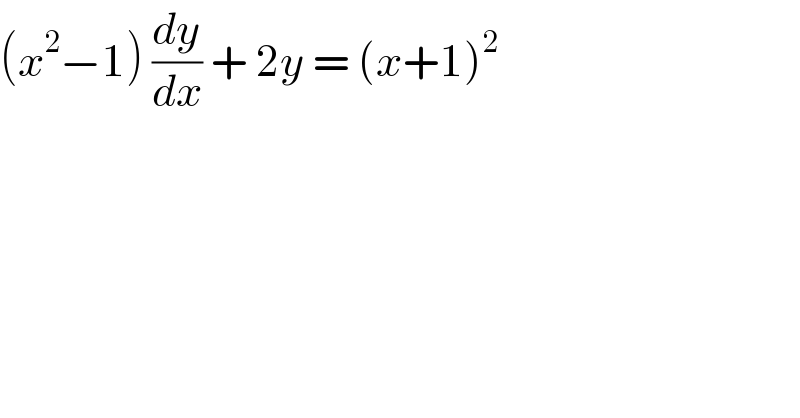
(x^2 −1) (dy/dx) + 2y = (x+1)^2

$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)\:\frac{{dy}}{{dx}}\:+\:\mathrm{2}{y}\:=\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$

Answered by bramlex last updated on 19/Jul/20

Commented by bramlex last updated on 19/Jul/20

typo integrating factor u(x) = e^(∫(2/((x+1)(x−1)))dx) = ((x−1)/(x+1)) (d/dx)((((x−1)/(x+1))).y)= ∫(((x−1)/(x+1)))(((x+1)/(x−1)))dx (((x−1)/(x+1)))y = ∫ dx (((x−1)/(x+1)))y = x +C ∴ y = ((x^2 +x)/(x−1)) +C(x−1)^(−1) ■

$${typo}\:{integrating}\:{factor}\: \\ $$$${u}\left({x}\right)\:=\:{e}^{\int\frac{\mathrm{2}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{dx}} =\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$\frac{{d}}{{dx}}\left(\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right).{y}\right)=\:\int\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right){dx} \\ $$$$\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right){y}\:=\:\int\:{dx}\: \\ $$$$\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right){y}\:=\:{x}\:+{C}\: \\ $$$$\therefore\:{y}\:=\:\frac{{x}^{\mathrm{2}} +{x}}{{x}−\mathrm{1}}\:+{C}\left({x}−\mathrm{1}\right)^{−\mathrm{1}} \:\blacksquare \\ $$

Answered by Dwaipayan Shikari last updated on 19/Jul/20

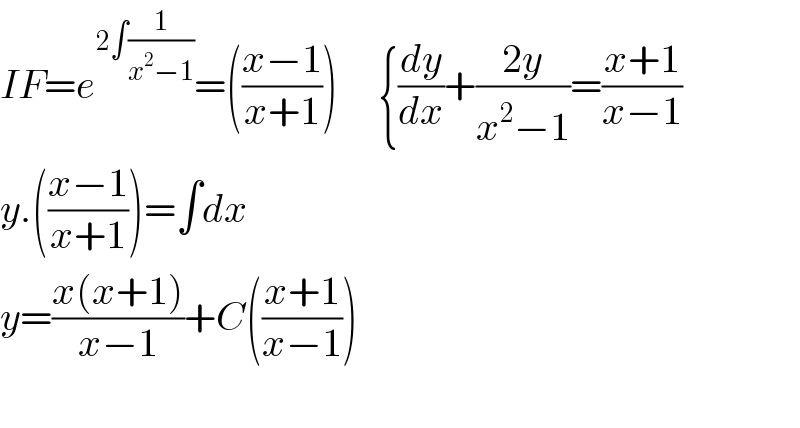
IF=e^(2∫(1/(x^2 −1))) =(((x−1)/(x+1))) {(dy/dx)+((2y)/(x^2 −1))=((x+1)/(x−1)) y.(((x−1)/(x+1)))=∫dx y=((x(x+1))/(x−1))+C(((x+1)/(x−1)))

$${IF}={e}^{\mathrm{2}\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}} =\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)\:\:\:\:\:\left\{\frac{{dy}}{{dx}}+\frac{\mathrm{2}{y}}{{x}^{\mathrm{2}} −\mathrm{1}}=\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right. \\ $$$${y}.\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)=\int{dx} \\ $$$${y}=\frac{{x}\left({x}+\mathrm{1}\right)}{{x}−\mathrm{1}}+{C}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 19/Jul/20

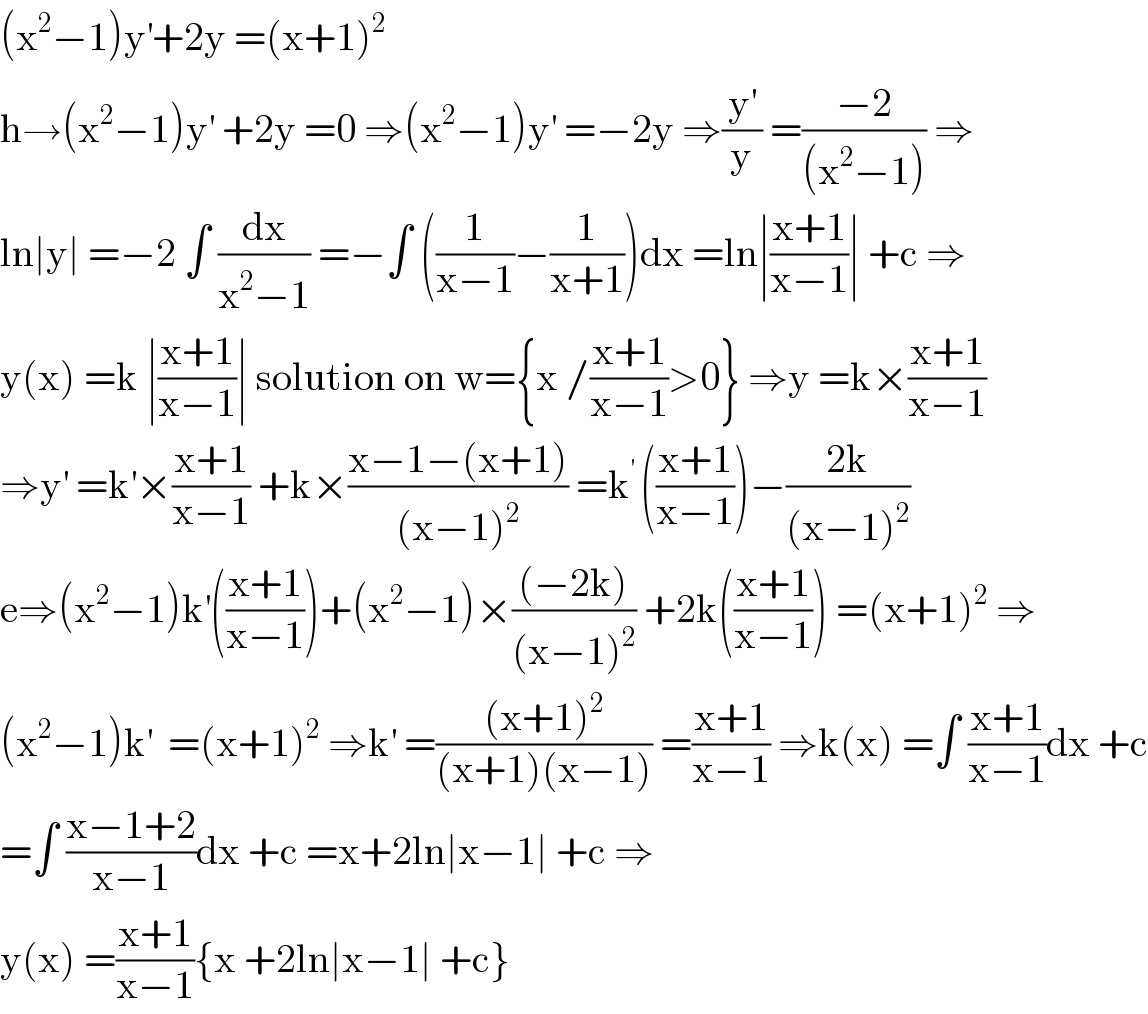
(x^2 −1)y^′ +2y =(x+1)^2 h→(x^2 −1)y^′ +2y =0 ⇒(x^2 −1)y^′ =−2y ⇒(y^′ /y) =((−2)/((x^2 −1))) ⇒ ln∣y∣ =−2 ∫ (dx/(x^2 −1)) =−∫ ((1/(x−1))−(1/(x+1)))dx =ln∣((x+1)/(x−1))∣ +c ⇒ y(x) =k ∣((x+1)/(x−1))∣ solution on w={x /((x+1)/(x−1))>0} ⇒y =k×((x+1)/(x−1)) ⇒y^′ =k^′ ×((x+1)/(x−1)) +k×((x−1−(x+1))/((x−1)^2 )) =k^(′ ) (((x+1)/(x−1)))−((2k)/((x−1)^2 )) e⇒(x^2 −1)k^′ (((x+1)/(x−1)))+(x^2 −1)×(((−2k))/((x−1)^2 )) +2k(((x+1)/(x−1))) =(x+1)^2 ⇒ (x^2 −1)k^′ =(x+1)^2 ⇒k^′ =(((x+1)^2 )/((x+1)(x−1))) =((x+1)/(x−1)) ⇒k(x) =∫ ((x+1)/(x−1))dx +c =∫ ((x−1+2)/(x−1))dx +c =x+2ln∣x−1∣ +c ⇒ y(x) =((x+1)/(x−1)){x +2ln∣x−1∣ +c}

$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{y}^{'} +\mathrm{2y}\:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{h}\rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{y}^{'} \:+\mathrm{2y}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{y}^{'} \:=−\mathrm{2y}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\frac{−\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{ln}\mid\mathrm{y}\mid\:=−\mathrm{2}\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=−\int\:\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\mathrm{dx}\:=\mathrm{ln}\mid\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{k}\:\mid\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mid\:\mathrm{solution}\:\mathrm{on}\:\mathrm{w}=\left\{\mathrm{x}\:/\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}>\mathrm{0}\right\}\:\Rightarrow\mathrm{y}\:=\mathrm{k}×\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} ×\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:+\mathrm{k}×\frac{\mathrm{x}−\mathrm{1}−\left(\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{k}^{'\:} \left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)−\frac{\mathrm{2k}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{e}\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{k}^{'} \left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)×\frac{\left(−\mathrm{2k}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\mathrm{2k}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)\:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{k}^{'} \:\:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{k}^{'} \:=\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right)}\:=\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:\Rightarrow\mathrm{k}\left(\mathrm{x}\right)\:=\int\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\:+\mathrm{c} \\ $$$$=\int\:\frac{\mathrm{x}−\mathrm{1}+\mathrm{2}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\:+\mathrm{c}\:=\mathrm{x}+\mathrm{2ln}\mid\mathrm{x}−\mathrm{1}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\left\{\mathrm{x}\:+\mathrm{2ln}\mid\mathrm{x}−\mathrm{1}\mid\:+\mathrm{c}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com