Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104086 by I want to learn more last updated on 19/Jul/20

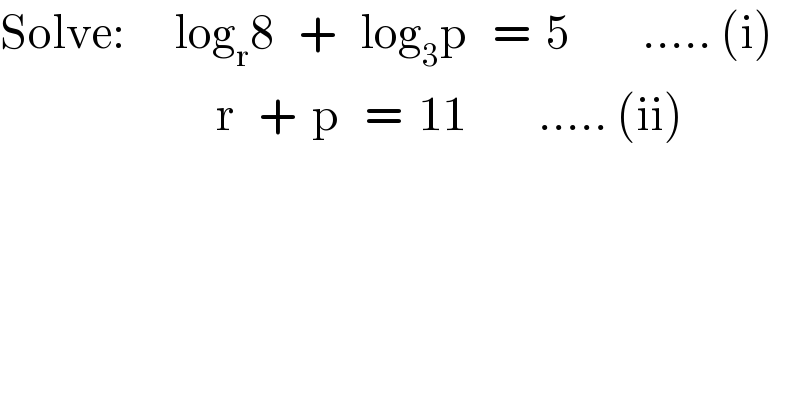
Solve: log_r 8 + log_3 p = 5 ..... (i) r + p = 11 ..... (ii)

$$\mathrm{Solve}:\:\:\:\:\:\:\mathrm{log}_{\mathrm{r}} \mathrm{8}\:\:\:+\:\:\:\mathrm{log}_{\mathrm{3}} \mathrm{p}\:\:\:=\:\:\mathrm{5}\:\:\:\:\:\:\:\:\:.....\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{r}\:\:\:+\:\:\mathrm{p}\:\:\:=\:\:\mathrm{11}\:\:\:\:\:\:\:\:\:.....\:\left(\mathrm{ii}\right) \\ $$

Commented by I want to learn more last updated on 19/Jul/20

Yes sir, but it is the workings i don′t know sir.

$$\mathrm{Yes}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{it}\:\mathrm{is}\:\mathrm{the}\:\mathrm{workings}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 19/Jul/20

i “see” the solution r=2, p=9. it is expected that you can see the solution, not calculate. if the second eqn. is r+p=12, you can not see and also not calculate the solution.

$${i}\:``{see}''\:{the}\:{solution}\:{r}=\mathrm{2},\:{p}=\mathrm{9}. \\ $$$${it}\:{is}\:{expected}\:{that}\:{you}\:{can}\:{see}\:{the} \\ $$$${solution},\:{not}\:{calculate}.\:{if}\:{the}\:{second} \\ $$$${eqn}.\:{is}\:{r}+{p}=\mathrm{12},\:{you}\:{can}\:{not}\:{see}\:{and} \\ $$$${also}\:{not}\:{calculate}\:{the}\:{solution}. \\ $$

Commented by I want to learn more last updated on 19/Jul/20

Alright. Thanks sir.

$$\mathrm{Alright}.\:\mathrm{Thanks}\:\:\mathrm{sir}. \\ $$

Answered by 1549442205PVT last updated on 19/Jul/20

Put log_r 8=a,log_3 p=b.We get 8=r^a ,p=3^b (r>0,r≠1,p>0) { ((a+b=5(1))),((3^b +8^(1/a) =11(2))) :} From (1) we get b=5−a ,replace into (2) we get 3^(5−a) +8^(1/a) −11=0(1).we need to have r=8^(1/a) <11⇒a>((ln8)/(ln11))≈0.8671. Putting f(a)=3^(5−a) +8^(1/a) −11.It is easy to see that f(3)=0,so a=3 is root of eqs.(1) we will prove it is unique root.Indeed, f ′(a)=−ln3×3^(5−a) +8^(1/a) (−(1/a^2 ))<0∀a∈(((ln8)/(ln11));+∞) hence a=3 is unique root of eqs.(1) ⇒b=2.From that we get r=2,p=9

$$\mathrm{Put}\:\mathrm{log}_{\mathrm{r}} \mathrm{8}=\mathrm{a},\mathrm{log}_{\mathrm{3}} \mathrm{p}=\mathrm{b}.\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{8}=\mathrm{r}^{\mathrm{a}} ,\mathrm{p}=\mathrm{3}^{\mathrm{b}} \:\left(\mathrm{r}>\mathrm{0},\mathrm{r}\neq\mathrm{1},\mathrm{p}>\mathrm{0}\right) \\ $$$$\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{5}\left(\mathrm{1}\right)}\\{\mathrm{3}^{\mathrm{b}} +\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{a}}} =\mathrm{11}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{b}=\mathrm{5}−\mathrm{a}\:,\mathrm{replace}\:\mathrm{into} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{3}^{\mathrm{5}−\mathrm{a}} +\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{a}}} −\mathrm{11}=\mathrm{0}\left(\mathrm{1}\right).\mathrm{we}\:\mathrm{need}\:\mathrm{to} \\ $$$$\mathrm{have}\:\mathrm{r}=\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{a}}} <\mathrm{11}\Rightarrow\mathrm{a}>\frac{\mathrm{ln8}}{\mathrm{ln11}}\approx\mathrm{0}.\mathrm{8671}. \\ $$$$\mathrm{Putting}\:\mathrm{f}\left(\mathrm{a}\right)=\mathrm{3}^{\mathrm{5}−\mathrm{a}} +\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{a}}} −\mathrm{11}.\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see} \\ $$$$\mathrm{that}\:\mathrm{f}\left(\mathrm{3}\right)=\mathrm{0},\mathrm{so}\:\mathrm{a}=\mathrm{3}\:\mathrm{is}\:\mathrm{root}\:\mathrm{of}\:\mathrm{eqs}.\left(\mathrm{1}\right) \\ $$$$\mathrm{we}\:\mathrm{will}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{is}\:\mathrm{unique}\:\mathrm{root}.\mathrm{Indeed}, \\ $$$$\mathrm{f}\:'\left(\mathrm{a}\right)=−\mathrm{ln3}×\mathrm{3}^{\mathrm{5}−\mathrm{a}} +\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{a}}} \left(−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\right)<\mathrm{0}\forall\mathrm{a}\in\left(\frac{\mathrm{ln8}}{\mathrm{ln11}};+\infty\right) \\ $$$$\mathrm{hence}\:\mathrm{a}=\mathrm{3}\:\mathrm{is}\:\mathrm{unique}\:\mathrm{root}\:\mathrm{of}\:\mathrm{eqs}.\left(\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{b}=\mathrm{2}.\mathrm{From}\:\mathrm{that}\:\mathrm{we}\:\mathrm{get}\:\boldsymbol{\mathrm{r}}=\mathrm{2},\boldsymbol{\mathrm{p}}=\mathrm{9} \\ $$

Commented by I want to learn more last updated on 19/Jul/20

I appreciate sir.

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com