Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 104092 by naka3546 last updated on 19/Jul/20

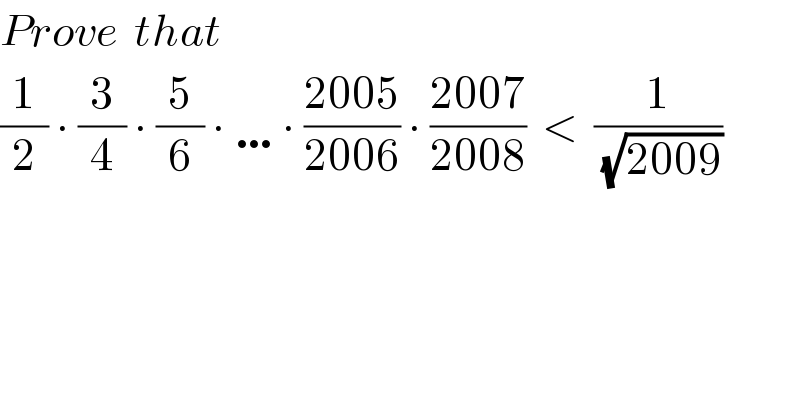
Prove that (1/2) ∙ (3/4) ∙ (5/6) ∙ …∙ ((2005)/(2006)) ∙ ((2007)/(2008)) < (1/(√(2009)))

$${Prove}\:\:{that}\:\: \\ $$ $$\frac{\mathrm{1}}{\mathrm{2}}\:\centerdot\:\frac{\mathrm{3}}{\mathrm{4}}\:\centerdot\:\frac{\mathrm{5}}{\mathrm{6}}\:\centerdot\:\ldots\centerdot\:\frac{\mathrm{2005}}{\mathrm{2006}}\:\centerdot\:\frac{\mathrm{2007}}{\mathrm{2008}}\:\:<\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{2009}}} \\ $$

Commented byJDamian last updated on 19/Jul/20

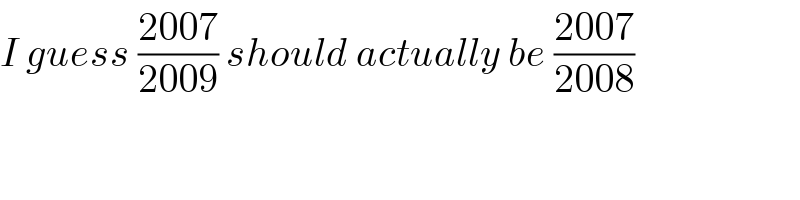
I guess ((2007)/(2009)) should actually be ((2007)/(2008))

$${I}\:{guess}\:\frac{\mathrm{2007}}{\mathrm{2009}}\:{should}\:{actually}\:{be}\:\frac{\mathrm{2007}}{\mathrm{2008}} \\ $$

Answered by 1549442205PVT last updated on 19/Jul/20

It is easy to see that if (a/b)<1 then a<b ⇒ab+a<ab+b⇒a(b+1)<b(a+1)⇒(a/b)<((a+1)/(b+1)). Hence, Putting A=(1/2).(3/4).(5/6)....((2005)/(2006)).((2007)/(2009)).We have: (1/2)<(2/3),(3/4)<(4/5),(5/6)<(6/7)...,((2005)/(2006))<((2006)/(2007)),((2007)/(2009))<((2009)/(2010)) Multiplying 1004 inequlities side by side we getA<(2/3).(4/5).(6/7)....((2006)/(2007)).((2009)/(2010))=B ⇒A^2 <AB=(1/2).(2/3).(3/4).(4/5).(5/6)....((2005)/(2006)).((2006)/(2007)).((2007)/(2009)).((2009)/(2010)) =(1/(2010))⇒A<(1/(√(2010)))<(1/(√(2009)))(q.e.d)

$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{if}\:\:\frac{\mathrm{a}}{\mathrm{b}}<\mathrm{1}\:\mathrm{then}\:\mathrm{a}<\mathrm{b} \\ $$ $$\Rightarrow\mathrm{ab}+\mathrm{a}<\mathrm{ab}+\mathrm{b}\Rightarrow\mathrm{a}\left(\mathrm{b}+\mathrm{1}\right)<\mathrm{b}\left(\mathrm{a}+\mathrm{1}\right)\Rightarrow\frac{\mathrm{a}}{\mathrm{b}}<\frac{\mathrm{a}+\mathrm{1}}{\mathrm{b}+\mathrm{1}}. \\ $$ $$\mathrm{Hence}, \\ $$ $$\mathrm{Putting}\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{5}}{\mathrm{6}}....\frac{\mathrm{2005}}{\mathrm{2006}}.\frac{\mathrm{2007}}{\mathrm{2009}}.\mathrm{We}\:\mathrm{have}: \\ $$ $$\frac{\mathrm{1}}{\mathrm{2}}<\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{4}}<\frac{\mathrm{4}}{\mathrm{5}},\frac{\mathrm{5}}{\mathrm{6}}<\frac{\mathrm{6}}{\mathrm{7}}...,\frac{\mathrm{2005}}{\mathrm{2006}}<\frac{\mathrm{2006}}{\mathrm{2007}},\frac{\mathrm{2007}}{\mathrm{2009}}<\frac{\mathrm{2009}}{\mathrm{2010}} \\ $$ $$\mathrm{Multiplying}\:\mathrm{1004}\:\mathrm{inequlities}\:\mathrm{side}\:\mathrm{by} \\ $$ $$\mathrm{side}\:\mathrm{we}\:\mathrm{getA}<\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{4}}{\mathrm{5}}.\frac{\mathrm{6}}{\mathrm{7}}....\frac{\mathrm{2006}}{\mathrm{2007}}.\frac{\mathrm{2009}}{\mathrm{2010}}=\mathrm{B} \\ $$ $$\Rightarrow\mathrm{A}^{\mathrm{2}} <\mathrm{AB}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{4}}{\mathrm{5}}.\frac{\mathrm{5}}{\mathrm{6}}....\frac{\mathrm{2005}}{\mathrm{2006}}.\frac{\mathrm{2006}}{\mathrm{2007}}.\frac{\mathrm{2007}}{\mathrm{2009}}.\frac{\mathrm{2009}}{\mathrm{2010}} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2010}}\Rightarrow\mathrm{A}<\frac{\mathrm{1}}{\sqrt{\mathrm{2010}}}<\frac{\mathrm{1}}{\sqrt{\mathrm{2009}}}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com