Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 104100 by bramlex last updated on 19/Jul/20

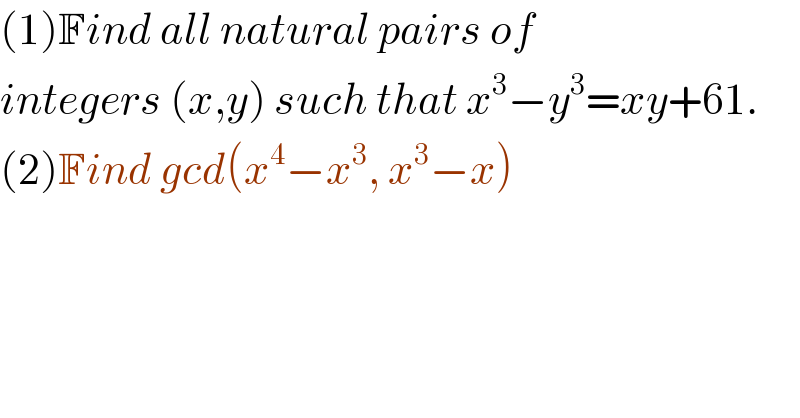
(1)Find all natural pairs of integers (x,y) such that x^3 −y^3 =xy+61. (2)Find gcd(x^4 −x^3 , x^3 −x)

$$\left(\mathrm{1}\right)\mathbb{F}{ind}\:{all}\:{natural}\:{pairs}\:{of} \\ $$$${integers}\:\left({x},{y}\right)\:{such}\:{that}\:{x}^{\mathrm{3}} −{y}^{\mathrm{3}} ={xy}+\mathrm{61}. \\ $$$$\left(\mathrm{2}\right)\mathbb{F}{ind}\:{gcd}\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} ,\:{x}^{\mathrm{3}} −{x}\right)\: \\ $$

Answered by bemath last updated on 19/Jul/20

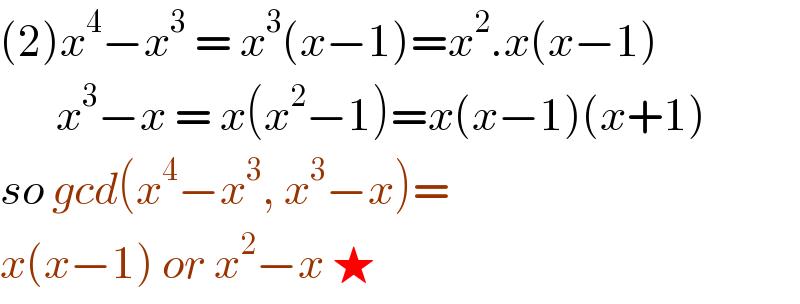
(2)x^4 −x^3 = x^3 (x−1)=x^2 .x(x−1) x^3 −x = x(x^2 −1)=x(x−1)(x+1) so gcd(x^4 −x^3 , x^3 −x)= x(x−1) or x^2 −x ★

$$\left(\mathrm{2}\right){x}^{\mathrm{4}} −{x}^{\mathrm{3}} \:=\:{x}^{\mathrm{3}} \left({x}−\mathrm{1}\right)={x}^{\mathrm{2}} .{x}\left({x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:{x}^{\mathrm{3}} −{x}\:=\:{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)={x}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right) \\ $$$${so}\:{gcd}\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} ,\:{x}^{\mathrm{3}} −{x}\right)= \\ $$$${x}\left({x}−\mathrm{1}\right)\:{or}\:{x}^{\mathrm{2}} −{x}\:\bigstar \\ $$

Answered by john santu last updated on 19/Jul/20

(1) x^3 −y^3 = (x−y)(x^2 +xy+y^2 ) ⇔(x−y)(x^2 +xy+y^2 )= xy+61 notice that x>y . therefore we have to consider x^2 +xy+y^2 ≤ xy+61 or x^2 +y^2 ≤ 61. because x>y , we have 61 ≥ x^2 +y^2 ≥2y^2 ⇒ y ∈{1,2,3,4,5} { ((y=1; x^3 −x−62=0)),((y=2; x^3 −2x−69=0)),((y=3; x^3 −3x−89=0)),((y=4; x^3 −4x−125=0)),((y=5; x^3 −5x−186=0; x=6)) :} we see the only working value for x is when x=6 ,y=5 ; so the only natural pairs of solution is (x,y) = (6,5) (JS ⊛)

$$\left(\mathrm{1}\right)\:{x}^{\mathrm{3}} −{y}^{\mathrm{3}} \:=\:\left({x}−{y}\right)\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\left({x}−{y}\right)\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)=\:{xy}+\mathrm{61} \\ $$$${notice}\:{that}\:{x}>{y}\:.\:{therefore}\:{we} \\ $$$${have}\:{to}\:{consider}\:{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \leqslant \\ $$$${xy}+\mathrm{61}\:{or}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\leqslant\:\mathrm{61}. \\ $$$${because}\:{x}>{y}\:,\:{we}\:{have}\: \\ $$$$\mathrm{61}\:\geqslant\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\geqslant\mathrm{2}{y}^{\mathrm{2}} \:\Rightarrow\:{y}\:\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right\} \\ $$$$\begin{cases}{{y}=\mathrm{1};\:{x}^{\mathrm{3}} −{x}−\mathrm{62}=\mathrm{0}}\\{{y}=\mathrm{2};\:{x}^{\mathrm{3}} −\mathrm{2}{x}−\mathrm{69}=\mathrm{0}}\\{{y}=\mathrm{3};\:{x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{89}=\mathrm{0}}\\{{y}=\mathrm{4};\:{x}^{\mathrm{3}} −\mathrm{4}{x}−\mathrm{125}=\mathrm{0}}\\{{y}=\mathrm{5};\:{x}^{\mathrm{3}} −\mathrm{5}{x}−\mathrm{186}=\mathrm{0};\:{x}=\mathrm{6}}\end{cases} \\ $$$${we}\:{see}\:{the}\:{only}\:{working}\:{value} \\ $$$${for}\:{x}\:{is}\:{when}\:{x}=\mathrm{6}\:,{y}=\mathrm{5}\:;\:{so}\:{the} \\ $$$${only}\:{natural}\:{pairs}\:{of}\:{solution} \\ $$$${is}\:\left({x},{y}\right)\:=\:\left(\mathrm{6},\mathrm{5}\right)\:\left({JS}\:\circledast\right)\: \\ $$

Commented by bramlex last updated on 19/Jul/20

thank you

$${thank}\:{you} \\ $$

Answered by floor(10²Eta[1]) last updated on 19/Jul/20

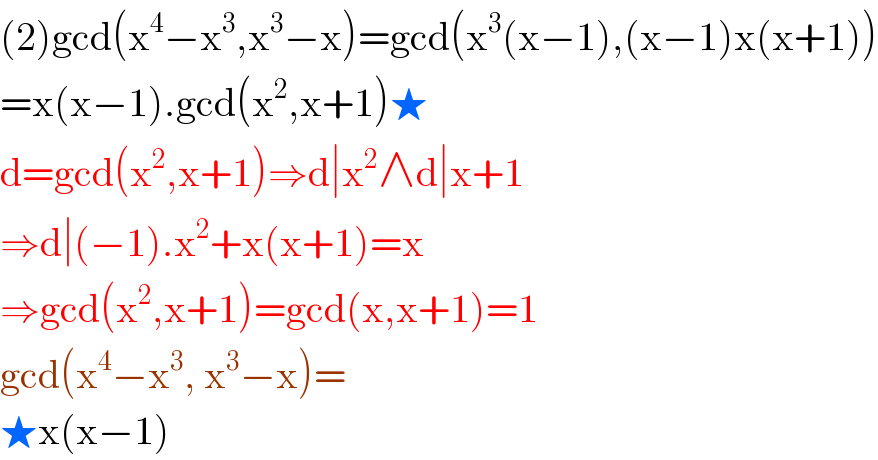
(2)gcd(x^4 −x^3 ,x^3 −x)=gcd(x^3 (x−1),(x−1)x(x+1)) =x(x−1).gcd(x^2 ,x+1)★ d=gcd(x^2 ,x+1)⇒d∣x^2 ∧d∣x+1 ⇒d∣(−1).x^2 +x(x+1)=x ⇒gcd(x^2 ,x+1)=gcd(x,x+1)=1 gcd(x^4 −x^3 , x^3 −x)= ★x(x−1)

$$\left(\mathrm{2}\right)\mathrm{gcd}\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} ,\mathrm{x}^{\mathrm{3}} −\mathrm{x}\right)=\mathrm{gcd}\left(\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}−\mathrm{1}\right),\left(\mathrm{x}−\mathrm{1}\right)\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\right) \\ $$$$=\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right).\mathrm{gcd}\left(\mathrm{x}^{\mathrm{2}} ,\mathrm{x}+\mathrm{1}\right)\bigstar \\ $$$$\mathrm{d}=\mathrm{gcd}\left(\mathrm{x}^{\mathrm{2}} ,\mathrm{x}+\mathrm{1}\right)\Rightarrow\mathrm{d}\mid\mathrm{x}^{\mathrm{2}} \wedge\mathrm{d}\mid\mathrm{x}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{d}\mid\left(−\mathrm{1}\right).\mathrm{x}^{\mathrm{2}} +\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{x} \\ $$$$\Rightarrow\mathrm{gcd}\left(\mathrm{x}^{\mathrm{2}} ,\mathrm{x}+\mathrm{1}\right)=\mathrm{gcd}\left(\mathrm{x},\mathrm{x}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{gcd}\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{3}} ,\:\mathrm{x}^{\mathrm{3}} −\mathrm{x}\right)= \\ $$$$\bigstar\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com