
Question Number 104122 by Dwaipayan Shikari last updated on 19/Jul/20
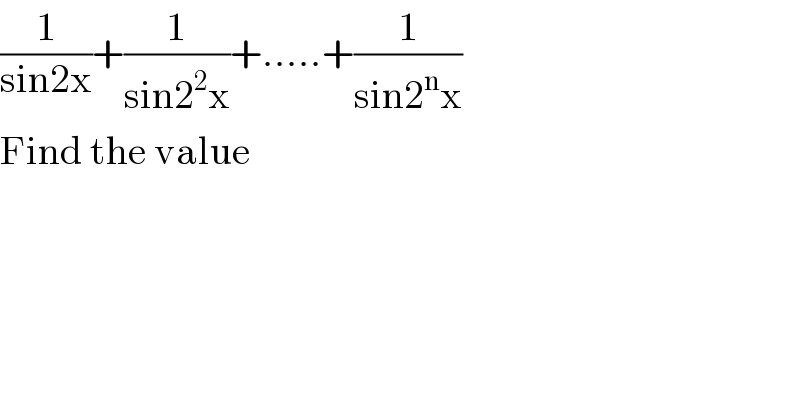
$$\frac{\mathrm{1}}{\mathrm{sin2x}}+\frac{\mathrm{1}}{\mathrm{sin2}^{\mathrm{2}} \mathrm{x}}+.....+\frac{\mathrm{1}}{\mathrm{sin2}^{\mathrm{n}} \mathrm{x}} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\: \\ $$
Answered by OlafThorendsen last updated on 19/Jul/20
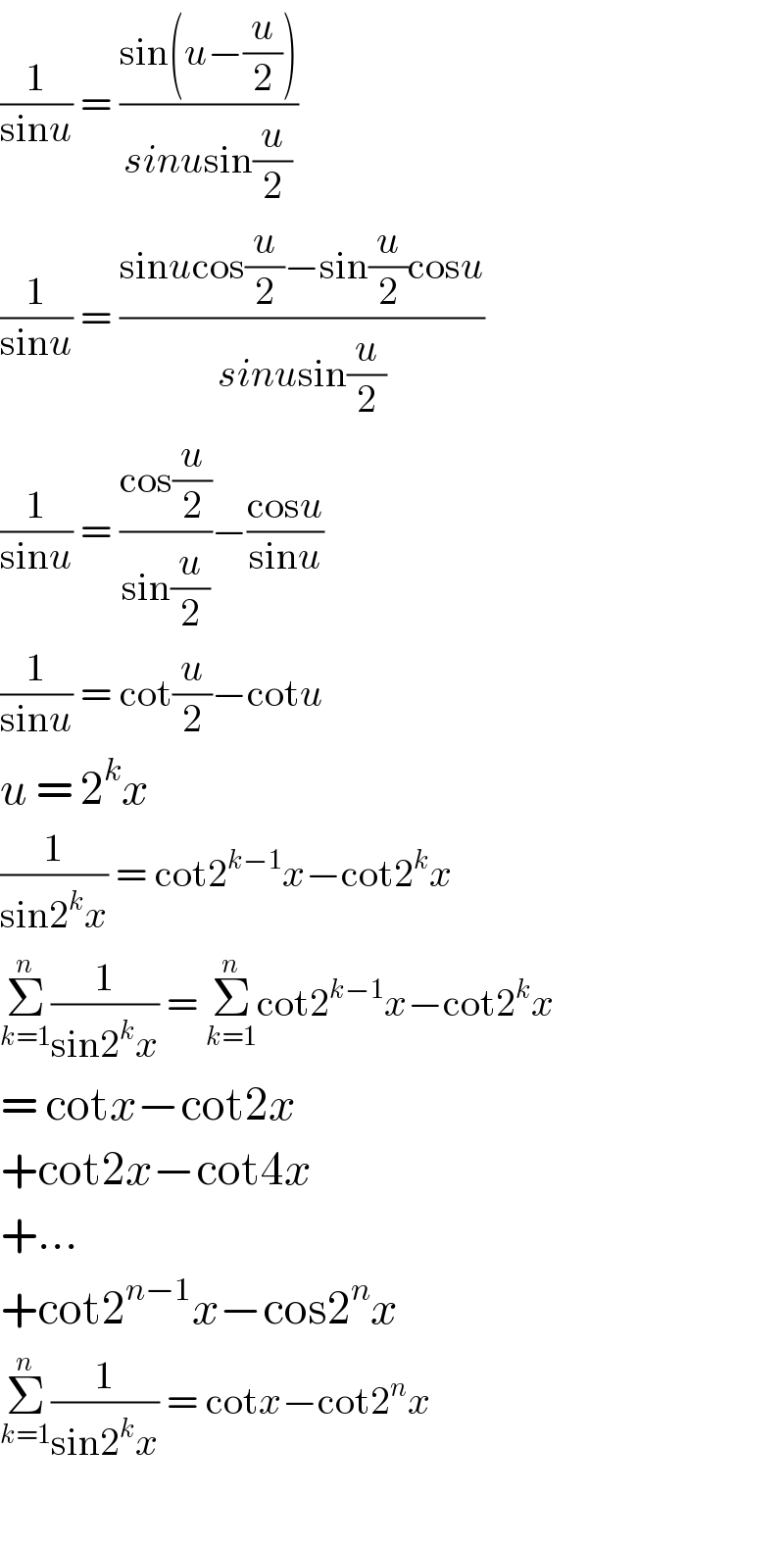
$$\frac{\mathrm{1}}{\mathrm{sin}{u}}\:=\:\frac{\mathrm{sin}\left({u}−\frac{{u}}{\mathrm{2}}\right)}{{sinu}\mathrm{sin}\frac{{u}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}{u}}\:=\:\frac{\mathrm{sin}{u}\mathrm{cos}\frac{{u}}{\mathrm{2}}−\mathrm{sin}\frac{{u}}{\mathrm{2}}\mathrm{cos}{u}}{{sinu}\mathrm{sin}\frac{{u}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}{u}}\:=\:\frac{\mathrm{cos}\frac{{u}}{\mathrm{2}}}{\mathrm{sin}\frac{{u}}{\mathrm{2}}}−\frac{\mathrm{cos}{u}}{\mathrm{sin}{u}} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}{u}}\:=\:\mathrm{cot}\frac{{u}}{\mathrm{2}}−\mathrm{cot}{u} \\ $$$${u}\:=\:\mathrm{2}^{{k}} {x} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin2}^{{k}} {x}}\:=\:\mathrm{cot2}^{{k}−\mathrm{1}} {x}−\mathrm{cot2}^{{k}} {x} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{sin2}^{{k}} {x}}\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cot2}^{{k}−\mathrm{1}} {x}−\mathrm{cot2}^{{k}} {x} \\ $$$$=\:\mathrm{cot}{x}−\mathrm{cot2}{x} \\ $$$$+\mathrm{cot2}{x}−\mathrm{cot4}{x} \\ $$$$+... \\ $$$$+\mathrm{cot2}^{{n}−\mathrm{1}} {x}−\mathrm{cos2}^{{n}} {x} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{sin2}^{{k}} {x}}\:=\:\mathrm{cot}{x}−\mathrm{cot2}^{{n}} {x} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 19/Jul/20

$$\mathrm{Great}\:\mathrm{sir}! \\ $$
