Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 104134 by bemath last updated on 19/Jul/20

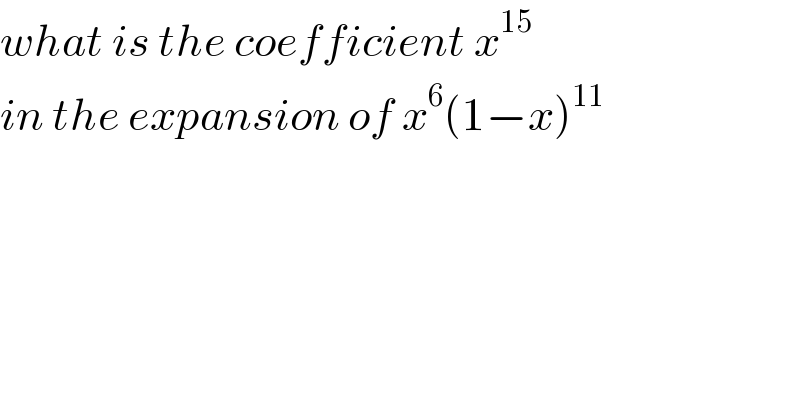
what is the coefficient x^(15) in the expansion of x^6 (1−x)^(11)

$${what}\:{is}\:{the}\:{coefficient}\:{x}^{\mathrm{15}} \\ $$$${in}\:{the}\:{expansion}\:{of}\:{x}^{\mathrm{6}} \left(\mathrm{1}−{x}\right)^{\mathrm{11}} \\ $$

Answered by bobhans last updated on 19/Jul/20

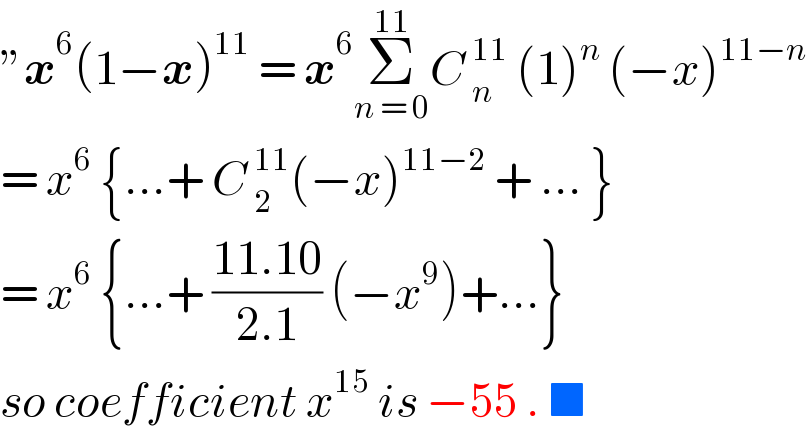
”x^6 (1−x)^(11) = x^6 Σ_(n = 0) ^(11) C _n^(11) (1)^n (−x)^(11−n) = x^6 {...+ C _2^(11) (−x)^(11−2) + ... } = x^6 {...+ ((11.10)/(2.1)) (−x^9 )+...} so coefficient x^(15) is −55 . ■

$$''\boldsymbol{{x}}^{\mathrm{6}} \left(\mathrm{1}−\boldsymbol{{x}}\right)^{\mathrm{11}} \:=\:\boldsymbol{{x}}^{\mathrm{6}} \underset{{n}\:=\:\mathrm{0}} {\overset{\mathrm{11}} {\sum}}{C}\:_{{n}} ^{\mathrm{11}} \:\left(\mathrm{1}\right)^{{n}} \:\left(−{x}\right)^{\mathrm{11}−{n}} \\ $$$$=\:{x}^{\mathrm{6}} \:\left\{...+\:{C}\:_{\mathrm{2}} ^{\mathrm{11}} \left(−{x}\right)^{\mathrm{11}−\mathrm{2}} \:+\:...\:\right\} \\ $$$$=\:{x}^{\mathrm{6}} \:\left\{...+\:\frac{\mathrm{11}.\mathrm{10}}{\mathrm{2}.\mathrm{1}}\:\left(−{x}^{\mathrm{9}} \right)+...\right\} \\ $$$${so}\:{coefficient}\:{x}^{\mathrm{15}} \:{is}\:−\mathrm{55}\:.\:\blacksquare\: \\ $$

Answered by mathmax by abdo last updated on 19/Jul/20

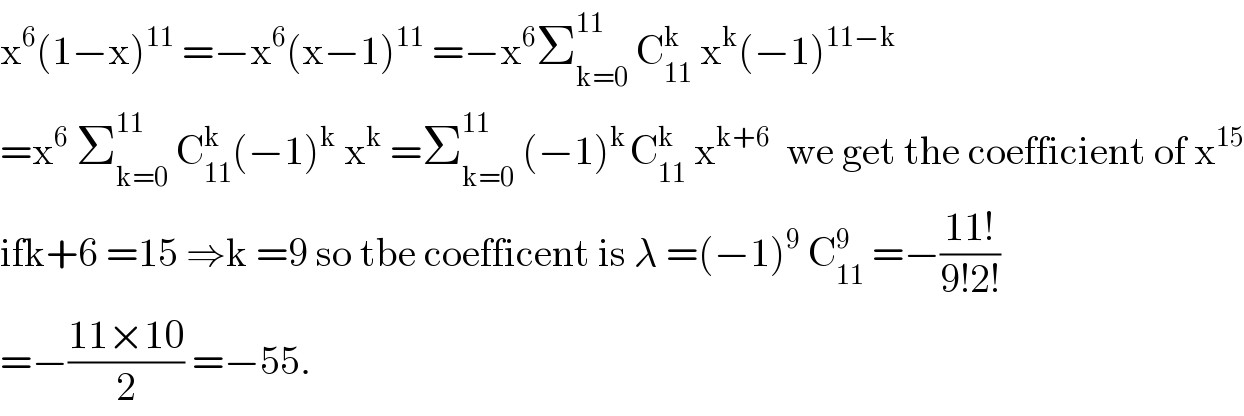
x^6 (1−x)^(11) =−x^6 (x−1)^(11) =−x^6 Σ_(k=0) ^(11 ) C_(11) ^k x^k (−1)^(11−k) =x^6 Σ_(k=0) ^(11) C_(11) ^k (−1)^k x^k =Σ_(k=0) ^(11) (−1)^(k ) C_(11) ^k x^(k+6) we get the coefficient of x^(15) ifk+6 =15 ⇒k =9 so tbe coefficent is λ =(−1)^9 C_(11) ^9 =−((11!)/(9!2!)) =−((11×10)/2) =−55.

$$\mathrm{x}^{\mathrm{6}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{11}} \:=−\mathrm{x}^{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{11}} \:=−\mathrm{x}^{\mathrm{6}} \sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}\:} \:\mathrm{C}_{\mathrm{11}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{11}−\mathrm{k}} \\ $$$$=\mathrm{x}^{\mathrm{6}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \:\mathrm{C}_{\mathrm{11}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \:\left(−\mathrm{1}\right)^{\mathrm{k}\:} \mathrm{C}_{\mathrm{11}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}+\mathrm{6}} \:\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{15}} \\ $$$$\mathrm{ifk}+\mathrm{6}\:=\mathrm{15}\:\Rightarrow\mathrm{k}\:=\mathrm{9}\:\mathrm{so}\:\mathrm{tbe}\:\mathrm{coefficent}\:\mathrm{is}\:\lambda\:=\left(−\mathrm{1}\right)^{\mathrm{9}} \:\mathrm{C}_{\mathrm{11}} ^{\mathrm{9}} \:=−\frac{\mathrm{11}!}{\mathrm{9}!\mathrm{2}!} \\ $$$$=−\frac{\mathrm{11}×\mathrm{10}}{\mathrm{2}}\:=−\mathrm{55}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com