Question Number 104139 by bobhans last updated on 19/Jul/20

what is remainder when 61^(61) divided by 1001

Commented byaurpeyz last updated on 19/Jul/20

how?

Answered by floor(10²Eta[1]) last updated on 19/Jul/20

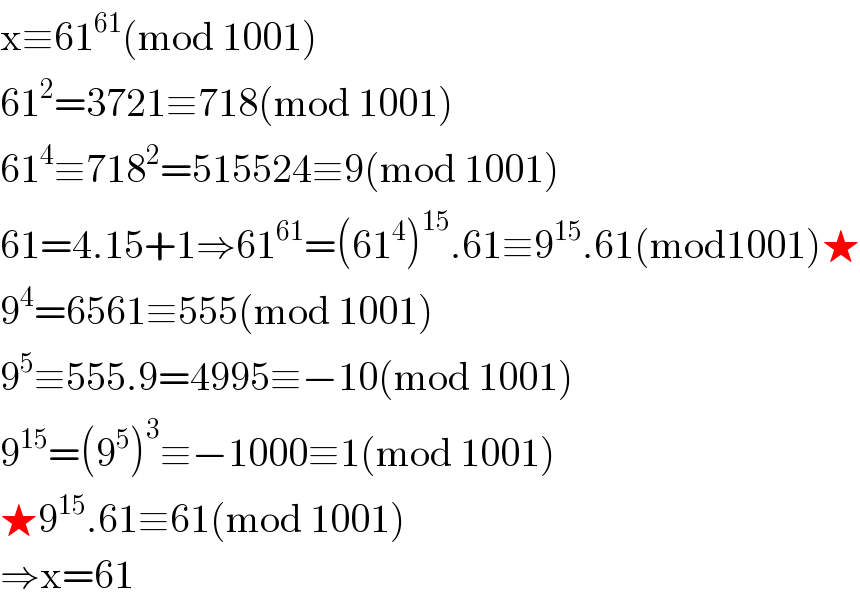
x≡61^(61) (mod 1001) 61^2 =3721≡718(mod 1001) 61^4 ≡718^2 =515524≡9(mod 1001) 61=4.15+1⇒61^(61) =(61^4 )^(15) .61≡9^(15) .61(mod1001)★ 9^4 =6561≡555(mod 1001) 9^5 ≡555.9=4995≡−10(mod 1001) 9^(15) =(9^5 )^3 ≡−1000≡1(mod 1001) ★9^(15) .61≡61(mod 1001) ⇒x=61

Answered by OlafThorendsen last updated on 19/Jul/20

61^(61) = 61.(61^2 )^(30) 61^(61) = 61.3721^(30) 61^(61) ≡ 61.718^(30) [1001] 61^(61) ≡ 61(718^2 )^(15) [1001] 61^(61) ≡ 61×(9)^(15) [1001] 61