Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 10414 by amir last updated on 07/Feb/17

Commented by mrW1 last updated on 08/Feb/17

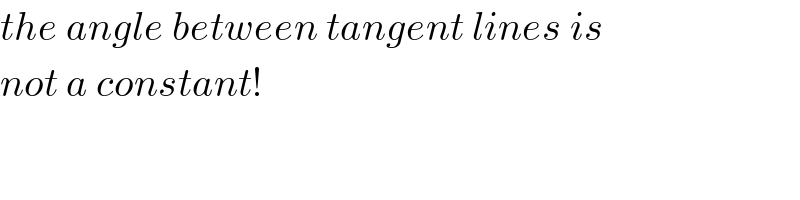
the angle between tangent lines is not a constant!

$${the}\:{angle}\:{between}\:{tangent}\:{lines}\:{is} \\ $$$${not}\:{a}\:{constant}! \\ $$

Commented by amir last updated on 08/Feb/17

hello dear mrW1.thank you so much for solving this problems. yes .you are right. angle is not constant and i shuld fix it.

$${hello}\:{dear}\:{mrW}\mathrm{1}.{thank}\:{you}\:{so}\:{much} \\ $$$${for}\:{solving}\:{this}\:{problems}. \\ $$$${yes}\:.{you}\:{are}\:{right}.\:{angle}\:{is}\:{not}\:{constant} \\ $$$${and}\:{i}\:{shuld}\:{fix}\:{it}. \\ $$

Answered by mrW1 last updated on 08/Feb/17

Q1: y=(1/x) y′=−(1/x^2 ) tangent line at point (t,(1/t)) on curve is y−(1/t)=−(1/t^2 )(x−t) since point (a,−a) lies on tangent line −a−(1/t)=−(1/t^2 )(a−t) at^2 +2t−a=0 t_(1,2) =((−2±(√(4+4a^2 )))/(2a))=((−1±(√(1+a^2 )))/a), a≠0 i.e. from point A(a,−a) with a≠0 there are 2 tangent lines: AD and AE D(t_1 ,(1/t_1 )) and E(t_2 ,(1/t_2 )) slope of AD=β_1 slope of AE=β_2 angle between tangent lines=β=β_2 −β_1 tan β_1 =−(1/t_1 ^2 )=−(1/((((−1+(√(1+a^2 )))/a))^2 ))=−(a^2 /(2+a^2 −2(√(1+a^2 )))) tan β_2 =−(1/t_2 ^2 )=−(1/((((−1−(√(1+a^2 )))/a))^2 ))=−(a^2 /(2+a^2 +2(√(1+a^2 )))) tan β=((−(a^2 /(2+a^2 +2(√(1+a^2 ))))+(a^2 /(2+a^2 −2(√(1+a^2 )))))/(1+(a^2 /(2+a^2 +2(√(1+a^2 ))))×(a^2 /(2+a^2 −2(√(1+a^2 )))))) =((a^2 (−2−a^2 +2(√(1+a^2 ))+2+a^2 +2(√(1+a^2 ))))/((2+a^2 +2(√(1+a^2 )))(2+a^2 −2(√(1+a^2 )))+a^4 )) =((4a^2 (√(1+a^2 )))/((2+a^2 )^2 −4(1+a^2 )+a^4 )) =((4a^2 (√(1+a^2 )))/(4+4a^2 +a^4 −4(1+a^2 )+a^4 )) =((2(√(1+a^2 )))/a^2 ) ⇒β=tan^(−1) (((2(√(1+a^2 )))/a^2 ))≠constant Q2: perpendicular line at point (t,(1/t)) on curve xy=1 is y−(1/t)=t^2 (x−t) since point A(a,−a) lies on the line −a−(1/t)=t^2 (a−t) t^4 −at^3 −at−1=0 (t^2 +1)(t^2 −at−1)=0 since t^2 +1≠0 ⇒t^2 −at−1=0 t_(1,2) =((a±(√(a^2 +4)))/2) i.e. from point A(a,−a) there are 2 perpendicular lines: AB and AC with B(t_1 ,(1/t_1 )) and C(t_2 ,(1/t_2 )) slope of AB=α_1 slope of AC=α_2 angle between them =α=α_2 −α_1 tan α_1 =t_1 ^2 =(((a+(√(a^2 +4)))/2))^2 =((a^2 +2+a(√(a^2 +4)))/2) tan α_2 =t_2 ^2 =(((a−(√(a^2 +4)))/2))^2 =((a^2 +2−a(√(a^2 +4)))/2) tan α=(((((a−(√(a^2 +4)))/2))^2 −(((a+(√(a^2 +4)))/2))^2 )/(1+(((a+(√(a^2 +4)))/2))^2 (((a−(√(a^2 +4)))/2))^2 )) =4×(((a−(√(a^2 +4)))^2 −(a+(√(a^2 +4)))^2 )/(16+(a+(√(a^2 +4)))^2 (a−(√(a^2 +4)))^2 )) =4×((−2a×2(√(a^2 +4)))/(16+(a^2 −a^2 −4)^2 )) =−((a(√(a^2 +4)))/2) ⇒α=tan^(−1) (−((a(√(a^2 +4)))/2)) angle between tangent line and perpendicular line=γ=β_1 −α_1 tan γ=((−(a^2 /(2+a^2 −2(√(1+a^2 ))))−((a^2 +2+a(√(a^2 +4)))/2))/(1+(a^2 /(2+a^2 −2(√(1+a^2 ))))×((a^2 +2+a(√(a^2 +4)))/2))) =−((2a^2 +(2+a^2 −2(√(1+a^2 )))(a^2 +2+a(√(a^2 +4))))/(2(2+a^2 −2(√(1+a^2 )))+a^2 (a^2 +2+a(√(a^2 +4))))) =−((2a^2 +(2+a^2 −2(√(1+a^2 )))(a^2 +2+a(√(a^2 +4))))/(4(1+a^2 )−4(√(1+a^2 ))+a^4 +a^3 (√(a^2 +4)))) ⇒γ=tan^(−1) (−((2a^2 +(2+a^2 −2(√(1+a^2 )))(a^2 +2+a(√(a^2 +4))))/(4(1+a^2 )−4(√(1+a^2 ))+a^4 +a^3 (√(a^2 +4)))))

$${Q}\mathrm{1}: \\ $$$${y}=\frac{\mathrm{1}}{{x}} \\ $$$${y}'=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${tangent}\:{line}\:{at}\:{point}\:\left({t},\frac{\mathrm{1}}{{t}}\right)\:{on}\:{curve} \\ $$$${is} \\ $$$${y}−\frac{\mathrm{1}}{{t}}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left({x}−{t}\right) \\ $$$${since}\:{point}\:\left({a},−{a}\right)\:{lies}\:{on}\:{tangent}\:{line} \\ $$$$−{a}−\frac{\mathrm{1}}{{t}}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left({a}−{t}\right) \\ $$$${at}^{\mathrm{2}} +\mathrm{2}{t}−{a}=\mathrm{0} \\ $$$${t}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{4}{a}^{\mathrm{2}} }}{\mathrm{2}{a}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}},\:{a}\neq\mathrm{0} \\ $$$${i}.{e}.\:{from}\:{point}\:{A}\left({a},−{a}\right)\:{with}\:{a}\neq\mathrm{0} \\ $$$${there}\:{are}\:\mathrm{2}\:{tangent}\:{lines}: \\ $$$${AD}\:{and}\:{AE} \\ $$$${D}\left({t}_{\mathrm{1}} ,\frac{\mathrm{1}}{{t}_{\mathrm{1}} }\right)\:{and}\:{E}\left({t}_{\mathrm{2}} ,\frac{\mathrm{1}}{{t}_{\mathrm{2}} }\right) \\ $$$${slope}\:{of}\:{AD}=\beta_{\mathrm{1}} \\ $$$${slope}\:{of}\:{AE}=\beta_{\mathrm{2}} \\ $$$${angle}\:{between}\:{tangent}\:{lines}=\beta=\beta_{\mathrm{2}} −\beta_{\mathrm{1}} \\ $$$$\mathrm{tan}\:\beta_{\mathrm{1}} =−\frac{\mathrm{1}}{{t}_{\mathrm{1}} ^{\mathrm{2}} }=−\frac{\mathrm{1}}{\left(\frac{−\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}}\right)^{\mathrm{2}} }=−\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\beta_{\mathrm{2}} =−\frac{\mathrm{1}}{{t}_{\mathrm{2}} ^{\mathrm{2}} }=−\frac{\mathrm{1}}{\left(\frac{−\mathrm{1}−\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}}\right)^{\mathrm{2}} }=−\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\beta=\frac{−\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}}{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}×\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}} \\ $$$$=\frac{{a}^{\mathrm{2}} \left(−\mathrm{2}−{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }+\mathrm{2}+{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)}{\left(\mathrm{2}+{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)\left(\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)+{a}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{4}{a}^{\mathrm{2}} \sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{\left(\mathrm{2}+{a}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)+{a}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{4}{a}^{\mathrm{2}} \sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{\mathrm{4}+\mathrm{4}{a}^{\mathrm{2}} +{a}^{\mathrm{4}} −\mathrm{4}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)+{a}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\beta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}^{\mathrm{2}} }\right)\neq{constant} \\ $$$$ \\ $$$${Q}\mathrm{2}: \\ $$$${perpendicular}\:{line}\:{at}\:{point}\:\left({t},\frac{\mathrm{1}}{{t}}\right) \\ $$$${on}\:{curve}\:{xy}=\mathrm{1}\:{is} \\ $$$${y}−\frac{\mathrm{1}}{{t}}={t}^{\mathrm{2}} \left({x}−{t}\right) \\ $$$${since}\:{point}\:{A}\left({a},−{a}\right)\:{lies}\:{on}\:{the}\:{line} \\ $$$$−{a}−\frac{\mathrm{1}}{{t}}={t}^{\mathrm{2}} \left({a}−{t}\right) \\ $$$${t}^{\mathrm{4}} −{at}^{\mathrm{3}} −{at}−\mathrm{1}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −{at}−\mathrm{1}\right)=\mathrm{0} \\ $$$${since}\:{t}^{\mathrm{2}} +\mathrm{1}\neq\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −{at}−\mathrm{1}=\mathrm{0} \\ $$$${t}_{\mathrm{1},\mathrm{2}} =\frac{{a}\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$${i}.{e}.\:{from}\:{point}\:{A}\left({a},−{a}\right)\:{there}\:{are} \\ $$$$\mathrm{2}\:{perpendicular}\:{lines}: \\ $$$${AB}\:{and}\:{AC}\:{with} \\ $$$${B}\left({t}_{\mathrm{1}} ,\frac{\mathrm{1}}{{t}_{\mathrm{1}} }\right)\:{and}\:{C}\left({t}_{\mathrm{2}} ,\frac{\mathrm{1}}{{t}_{\mathrm{2}} }\right) \\ $$$${slope}\:{of}\:{AB}=\alpha_{\mathrm{1}} \\ $$$${slope}\:{of}\:{AC}=\alpha_{\mathrm{2}} \\ $$$${angle}\:{between}\:{them}\:=\alpha=\alpha_{\mathrm{2}} −\alpha_{\mathrm{1}} \\ $$$$\mathrm{tan}\:\alpha_{\mathrm{1}} ={t}_{\mathrm{1}} ^{\mathrm{2}} =\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha_{\mathrm{2}} ={t}_{\mathrm{2}} ^{\mathrm{2}} =\left(\frac{{a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +\mathrm{2}−{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\left(\frac{{a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\frac{{a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{4}×\frac{\left({a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} −\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} }{\mathrm{16}+\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} \left({a}−\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{4}×\frac{−\mathrm{2}{a}×\mathrm{2}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{16}+\left({a}^{\mathrm{2}} −{a}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$=−\frac{{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\mathrm{tan}^{−\mathrm{1}} \left(−\frac{{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right) \\ $$$$ \\ $$$${angle}\:{between}\:{tangent}\:{line}\:{and} \\ $$$${perpendicular}\:{line}=\gamma=\beta_{\mathrm{1}} −\alpha_{\mathrm{1}} \\ $$$$\mathrm{tan}\:\gamma=\frac{−\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}−\frac{{a}^{\mathrm{2}} +\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}}{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}×\frac{{a}^{\mathrm{2}} +\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{2}{a}^{\mathrm{2}} +\left(\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)\left({a}^{\mathrm{2}} +\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)}{\mathrm{2}\left(\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)+{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)}\: \\ $$$$=−\frac{\mathrm{2}{a}^{\mathrm{2}} +\left(\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)\left({a}^{\mathrm{2}} +\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)}{\mathrm{4}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)−\mathrm{4}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }+{a}^{\mathrm{4}} +{a}^{\mathrm{3}} \sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}\: \\ $$$$\Rightarrow\gamma=\mathrm{tan}^{−\mathrm{1}} \left(−\frac{\mathrm{2}{a}^{\mathrm{2}} +\left(\mathrm{2}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)\left({a}^{\mathrm{2}} +\mathrm{2}+{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)}{\mathrm{4}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)−\mathrm{4}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }+{a}^{\mathrm{4}} +{a}^{\mathrm{3}} \sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}\right) \\ $$

Commented by mrW1 last updated on 08/Feb/17

Answered by mrW1 last updated on 08/Feb/17

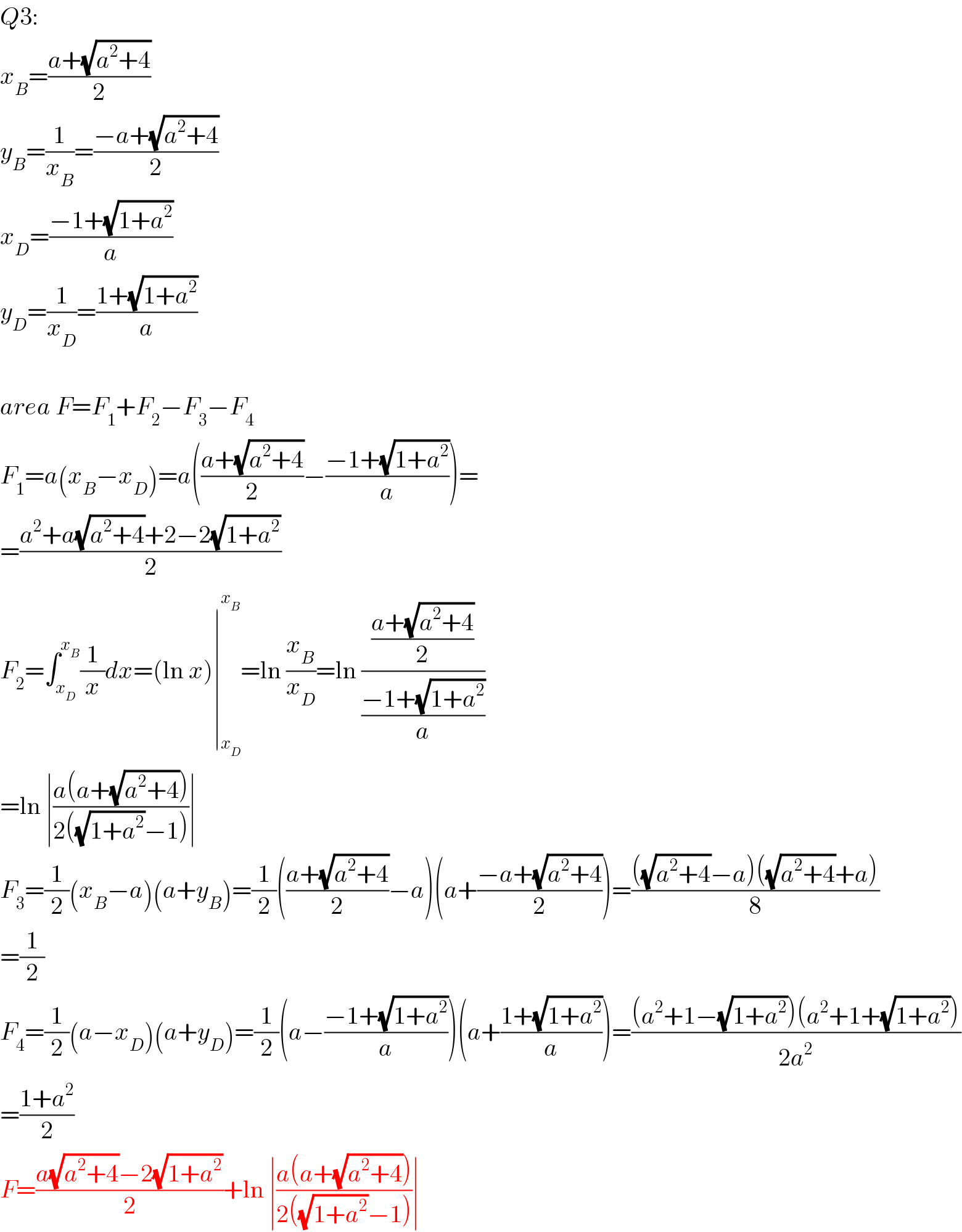
Q3: x_B =((a+(√(a^2 +4)))/2) y_B =(1/x_B )=((−a+(√(a^2 +4)))/2) x_D =((−1+(√(1+a^2 )))/a) y_D =(1/x_D )=((1+(√(1+a^2 )))/a) area F=F_1 +F_2 −F_3 −F_4 F_1 =a(x_B −x_D )=a(((a+(√(a^2 +4)))/2)−((−1+(√(1+a^2 )))/a))= =((a^2 +a(√(a^2 +4))+2−2(√(1+a^2 )))/2) F_2 =∫_x_D ^x_B (1/x)dx=(ln x)∣_x_D ^x_B =ln (x_B /x_D )=ln (((a+(√(a^2 +4)))/2)/((−1+(√(1+a^2 )))/a)) =ln ∣((a(a+(√(a^2 +4))))/(2((√(1+a^2 ))−1)))∣ F_3 =(1/2)(x_B −a)(a+y_B )=(1/2)(((a+(√(a^2 +4)))/2)−a)(a+((−a+(√(a^2 +4)))/2))=((((√(a^2 +4))−a)((√(a^2 +4))+a))/8) =(1/2) F_4 =(1/2)(a−x_D )(a+y_D )=(1/2)(a−((−1+(√(1+a^2 )))/a))(a+((1+(√(1+a^2 )))/a))=(((a^2 +1−(√(1+a^2 )))(a^2 +1+(√(1+a^2 ))))/(2a^2 )) =((1+a^2 )/2) F=((a(√(a^2 +4))−2(√(1+a^2 )))/2)+ln ∣((a(a+(√(a^2 +4))))/(2((√(1+a^2 ))−1)))∣

$${Q}\mathrm{3}: \\ $$$${x}_{{B}} =\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$${y}_{{B}} =\frac{\mathrm{1}}{{x}_{{B}} }=\frac{−{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$$${x}_{{D}} =\frac{−\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}} \\ $$$${y}_{{D}} =\frac{\mathrm{1}}{{x}_{{D}} }=\frac{\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}} \\ $$$$ \\ $$$${area}\:{F}={F}_{\mathrm{1}} +{F}_{\mathrm{2}} −{F}_{\mathrm{3}} −{F}_{\mathrm{4}} \\ $$$${F}_{\mathrm{1}} ={a}\left({x}_{{B}} −{x}_{{D}} \right)={a}\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}−\frac{−\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}}\right)= \\ $$$$=\frac{{a}^{\mathrm{2}} +{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}+\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${F}_{\mathrm{2}} =\int_{{x}_{{D}} } ^{{x}_{{B}} } \frac{\mathrm{1}}{{x}}{dx}=\left(\mathrm{ln}\:{x}\right)\mid_{{x}_{{D}} } ^{{x}_{{B}} } =\mathrm{ln}\:\frac{{x}_{{B}} }{{x}_{{D}} }=\mathrm{ln}\:\frac{\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}}{\frac{−\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}}} \\ $$$$=\mathrm{ln}\:\mid\frac{{a}\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)}{\mathrm{2}\left(\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }−\mathrm{1}\right)}\mid \\ $$$${F}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left({x}_{{B}} −{a}\right)\left({a}+{y}_{{B}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}−{a}\right)\left({a}+\frac{−{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\right)=\frac{\left(\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}−{a}\right)\left(\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}+{a}\right)}{\mathrm{8}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{x}_{{D}} \right)\left({a}+{y}_{{D}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left({a}−\frac{−\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}}\right)\left({a}+\frac{\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{{a}}\right)=\frac{\left({a}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)\left({a}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\right)}{\mathrm{2}{a}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}+{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${F}=\frac{{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}−\mathrm{2}\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}{\mathrm{2}}+\mathrm{ln}\:\mid\frac{{a}\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)}{\mathrm{2}\left(\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }−\mathrm{1}\right)}\mid \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com