Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 104157 by ajfour last updated on 19/Jul/20

Commented by ajfour last updated on 19/Jul/20

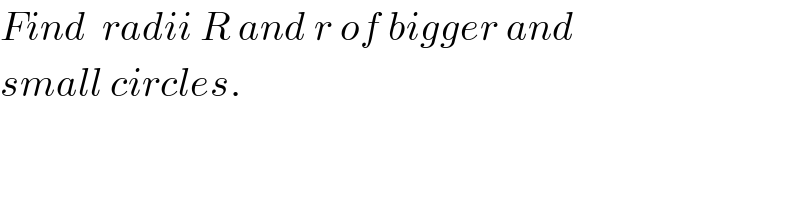
$$FindradiiRandrofbiggerand$$$$smallcircles.$$

Answered by mr W last updated on 19/Jul/20

$$H(1,1)$$$$OH=\sqrt{2}R+R=\sqrt{2}$$$$\Rightarrow R=\frac{\sqrt{2}}{\sqrt{2}+1}=2-\sqrt{2}$$$$D(R+2\sqrt{Rr},r)=(h,r)$$$$F(k,\frac{1}{k})$$$$\tan \theta =\frac{1}{k^2}$$$$k=h+r\sin \theta =R+2\sqrt{Rr}+r\frac{1}{\sqrt{1+k^4}}$$$$\frac{1}{k}=r+r\cos \theta =r(1+\frac{k^2}{\sqrt{1+k^4}})$$$$\Rightarrow r=\frac{1}{k(1+\frac{k^2}{\sqrt{1+k^4}})}$$$$k=R+2\sqrt{\frac{R}{k(1+\frac{k^2}{\sqrt{1+k^4}})}}+\frac{1}{k(\sqrt{1+k^4}+k^2)}$$$$\Rightarrow k\approx 1.5831$$$$\Rightarrow r\approx 0.3275$$

Commented by mr W last updated on 19/Jul/20

Commented by ajfour last updated on 19/Jul/20

$$Itoothink,thisasthepossibleway,$$$$Sir,thanksforthesolution!$$

Answered by ajfour last updated on 21/Jul/20

Commented by ajfour last updated on 22/Jul/20

$$R=2-\sqrt{2}$$$$C(0,R\sqrt{2})$$$$lety-x=s,y+x=t$$$$\Rightarrow y=\frac{s+t}{2},\frac{1}{x}=\frac{2}{t-s}$$$$y=\frac{1}{x}is{t}^2-s^2=4$$$$s=\sqrt{t^2-4}$$$$A(\frac{R}{\sqrt{2}}+\sqrt{2Rr},\frac{R}{\sqrt{2}}+\sqrt{2Rr})$$$$D(\frac{R}{\sqrt{2}}+\sqrt{2Rr}-\frac{r}{\sqrt{2}},\frac{R}{\sqrt{2}}+\sqrt{2Rr}+\frac{r}{\sqrt{2}})$$$$.....$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com