Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 104174 by Dwaipayan Shikari last updated on 19/Jul/20

$$\underset{\mathrm{n}=1}{\prod ^{\mathrm{\infty }}}{\left(\frac{\mathrm{n}}{\mathrm{n}+1}\right)}^2$$

Answered by OlafThorendsen last updated on 19/Jul/20

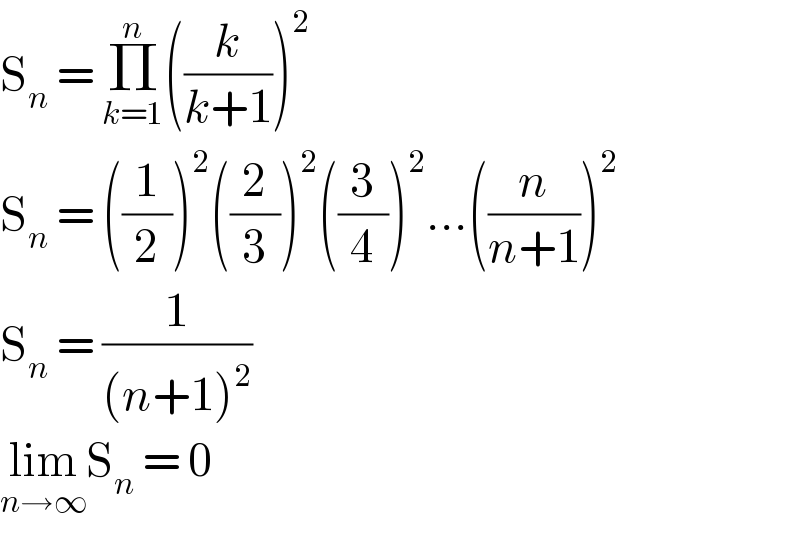
$${\mathrm{S}}_n=\underset{k=1}{\prod ^n}{\left(\frac{k}{k+1}\right)}^2$$$${\mathrm{S}}_n={\left(\frac{1}{2}\right)}^2{\left(\frac{2}{3}\right)}^2{\left(\frac{3}{4}\right)}^2...{\left(\frac{n}{n+1}\right)}^2$$$${\mathrm{S}}_n=\frac{1}{{(n+1)}^2}$$$$\text{Double subscripts: use braces to clarify}$$

Answered by mathmax by abdo last updated on 19/Jul/20

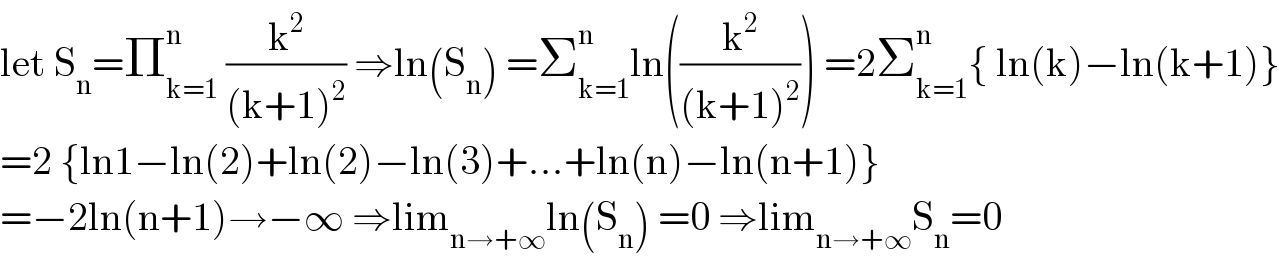
$$\mathrm{let}{\mathrm{S}}_{\mathrm{n}}=\prod _{\mathrm{k}=1}^{\mathrm{n}}\frac{{\mathrm{k}}^2}{{(\mathrm{k}+1)}^2}\Rightarrow \ln \left({\mathrm{S}}_{\mathrm{n}}\right)=\sum _{\mathrm{k}=1}^{\mathrm{n}}\ln \left(\frac{{\mathrm{k}}^2}{{(\mathrm{k}+1)}^2}\right)=2\sum _{\mathrm{k}=1}^{\mathrm{n}}\{\ln \left(\mathrm{k}\right)-\ln (\mathrm{k}+1)\}$$$$=2\{\ln 1-\ln \left(2\right)+\ln \left(2\right)-\ln \left(3\right)+...+\ln \left(\mathrm{n}\right)-\ln (\mathrm{n}+1)\}$$$$=-2\ln (\mathrm{n}+1)\to -\mathrm{\infty }\Rightarrow {\lim }_{\mathrm{n}\to +\mathrm{\infty }}\ln \left({\mathrm{S}}_{\mathrm{n}}\right)=0\Rightarrow {\lim }_{\mathrm{n}\to +\mathrm{\infty }}{\mathrm{S}}_{\mathrm{n}}=0$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com