Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 104181 by mathocean1 last updated on 19/Jul/20

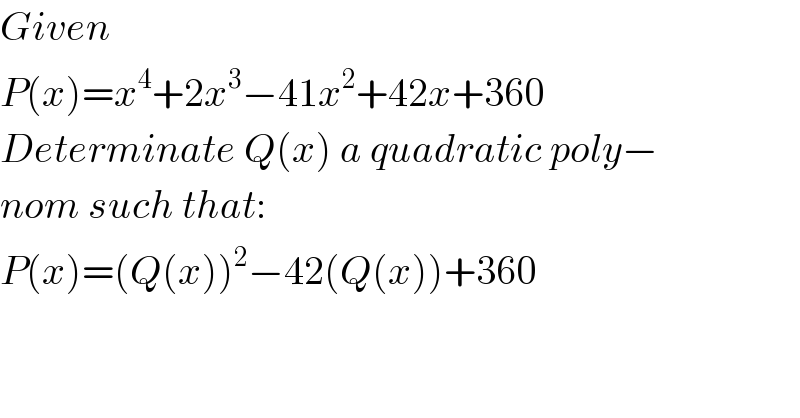
Given P(x)=x^4 +2x^3 −41x^2 +42x+360 Determinate Q(x) a quadratic poly− nom such that: P(x)=(Q(x))^2 −42(Q(x))+360

$${Given} \\ $$$${P}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{41}{x}^{\mathrm{2}} +\mathrm{42}{x}+\mathrm{360} \\ $$$${Determinate}\:{Q}\left({x}\right)\:{a}\:{quadratic}\:{poly}− \\ $$$${nom}\:{such}\:{that}: \\ $$$${P}\left({x}\right)=\left({Q}\left({x}\right)\right)^{\mathrm{2}} −\mathrm{42}\left({Q}\left({x}\right)\right)+\mathrm{360} \\ $$

Answered by mr W last updated on 19/Jul/20

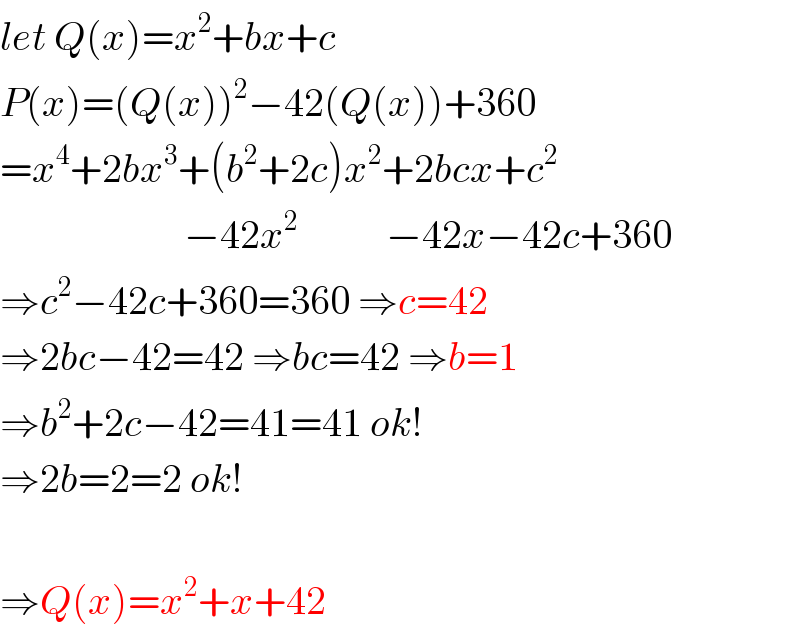
let Q(x)=x^2 +bx+c P(x)=(Q(x))^2 −42(Q(x))+360 =x^4 +2bx^3 +(b^2 +2c)x^2 +2bcx+c^2 −42x^2 −42x−42c+360 ⇒c^2 −42c+360=360 ⇒c=42 ⇒2bc−42=42 ⇒bc=42 ⇒b=1 ⇒b^2 +2c−42=41=41 ok! ⇒2b=2=2 ok! ⇒Q(x)=x^2 +x+42

$${let}\:{Q}\left({x}\right)={x}^{\mathrm{2}} +{bx}+{c} \\ $$$${P}\left({x}\right)=\left({Q}\left({x}\right)\right)^{\mathrm{2}} −\mathrm{42}\left({Q}\left({x}\right)\right)+\mathrm{360} \\ $$$$={x}^{\mathrm{4}} +\mathrm{2}{bx}^{\mathrm{3}} +\left({b}^{\mathrm{2}} +\mathrm{2}{c}\right){x}^{\mathrm{2}} +\mathrm{2}{bcx}+{c}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{42}{x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:−\mathrm{42}{x}−\mathrm{42}{c}+\mathrm{360} \\ $$$$\Rightarrow{c}^{\mathrm{2}} −\mathrm{42}{c}+\mathrm{360}=\mathrm{360}\:\Rightarrow{c}=\mathrm{42} \\ $$$$\Rightarrow\mathrm{2}{bc}−\mathrm{42}=\mathrm{42}\:\Rightarrow{bc}=\mathrm{42}\:\Rightarrow{b}=\mathrm{1} \\ $$$$\Rightarrow{b}^{\mathrm{2}} +\mathrm{2}{c}−\mathrm{42}=\mathrm{41}=\mathrm{41}\:{ok}! \\ $$$$\Rightarrow\mathrm{2}{b}=\mathrm{2}=\mathrm{2}\:{ok}! \\ $$$$ \\ $$$$\Rightarrow{Q}\left({x}\right)={x}^{\mathrm{2}} +{x}+\mathrm{42} \\ $$

Commented by mathocean1 last updated on 19/Jul/20

thank you sir!

$${thank}\:{you}\:{sir}! \\ $$

Commented by mathocean1 last updated on 19/Jul/20

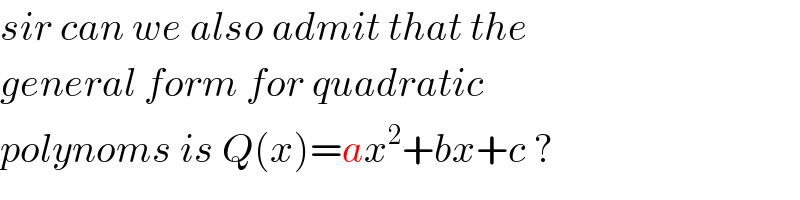
sir can we also admit that the general form for quadratic polynoms is Q(x)=ax^2 +bx+c ?

$${sir}\:{can}\:{we}\:{also}\:{admit}\:{that}\:{the} \\ $$$${general}\:{form}\:{for}\:{quadratic} \\ $$$${polynoms}\:{is}\:{Q}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}\:? \\ $$

Commented by mr W last updated on 19/Jul/20

yes, but here it′s obvious that a=1.

$${yes},\:{but}\:{here}\:{it}'{s}\:{obvious}\:{that}\:{a}=\mathrm{1}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com