Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 104199 by hardylanes last updated on 20/Jul/20

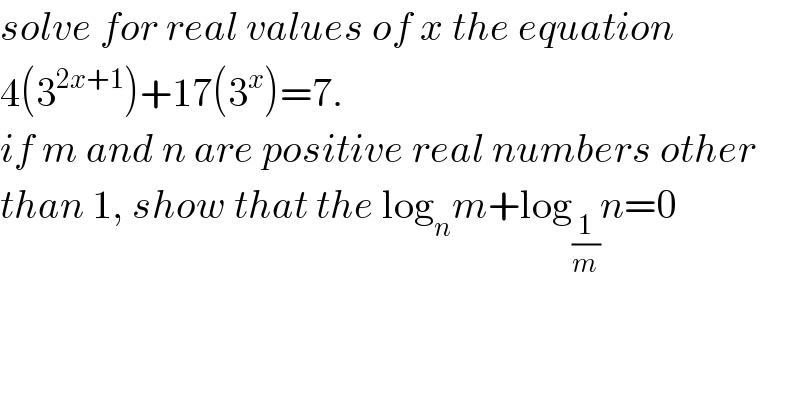
solve for real values of x the equation 4(3^(2x+1) )+17(3^x )=7. if m and n are positive real numbers other than 1, show that the log_n m+log_(1/m) n=0

$${solve}\:{for}\:{real}\:{values}\:{of}\:{x}\:{the}\:{equation} \\ $$$$\mathrm{4}\left(\mathrm{3}^{\mathrm{2}{x}+\mathrm{1}} \right)+\mathrm{17}\left(\mathrm{3}^{{x}} \right)=\mathrm{7}. \\ $$$${if}\:{m}\:{and}\:{n}\:{are}\:{positive}\:{real}\:{numbers}\:{other} \\ $$$${than}\:\mathrm{1},\:{show}\:{that}\:{the}\:\mathrm{log}_{{n}} {m}+\mathrm{log}_{\frac{\mathrm{1}}{{m}}} {n}=\mathrm{0} \\ $$

Answered by bemath last updated on 20/Jul/20

12.3^x +17.3^x −7=0 3^x = ((−17+(√(289+48.7)))/(24)) 3^x = ((−17+25)/(24)) = (1/3) ∴ x = −1

$$\mathrm{12}.\mathrm{3}^{{x}} +\mathrm{17}.\mathrm{3}^{{x}} −\mathrm{7}=\mathrm{0} \\ $$$$\mathrm{3}^{{x}} =\:\frac{−\mathrm{17}+\sqrt{\mathrm{289}+\mathrm{48}.\mathrm{7}}}{\mathrm{24}} \\ $$$$\mathrm{3}^{{x}} \:=\:\frac{−\mathrm{17}+\mathrm{25}}{\mathrm{24}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\therefore\:{x}\:=\:−\mathrm{1} \\ $$

Answered by OlafThorendsen last updated on 20/Jul/20

4(3^(2x+1) )+17(3^x ) = 7 12(3^x )^2 +17(3^x )−7 = 0 u = 3^x 12u^2 +17u−7 = 0 Δ = 17^2 −4×12×(−7) = 625 = 25^2 u = ((−17±25)/(24)) u = 3^x ⇒ u>0 then u = ((−17+25)/(24)) = (1/3) u = 3^x = (1/3) ⇒ x = −1 I think your second question is false (it′s true only for m = n or m = (1/n)) but : log_n m+log_(1/n) m = ((lnm)/(lnn))+((lnm)/(ln(1/n))) = ((lnm)/(lnn))−((lnm)/(lnn)) = 0

$$\mathrm{4}\left(\mathrm{3}^{\mathrm{2}{x}+\mathrm{1}} \right)+\mathrm{17}\left(\mathrm{3}^{{x}} \right)\:=\:\mathrm{7} \\ $$$$\mathrm{12}\left(\mathrm{3}^{{x}} \right)^{\mathrm{2}} +\mathrm{17}\left(\mathrm{3}^{{x}} \right)−\mathrm{7}\:=\:\mathrm{0} \\ $$$${u}\:=\:\mathrm{3}^{{x}} \\ $$$$\mathrm{12}{u}^{\mathrm{2}} +\mathrm{17}{u}−\mathrm{7}\:=\:\mathrm{0} \\ $$$$\Delta\:=\:\mathrm{17}^{\mathrm{2}} −\mathrm{4}×\mathrm{12}×\left(−\mathrm{7}\right)\:=\:\mathrm{625}\:=\:\mathrm{25}^{\mathrm{2}} \\ $$$${u}\:=\:\frac{−\mathrm{17}\pm\mathrm{25}}{\mathrm{24}} \\ $$$${u}\:=\:\mathrm{3}^{{x}} \:\Rightarrow\:{u}>\mathrm{0} \\ $$$$\mathrm{then}\:{u}\:=\:\frac{−\mathrm{17}+\mathrm{25}}{\mathrm{24}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${u}\:=\:\mathrm{3}^{{x}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{x}\:=\:−\mathrm{1} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{your}\:\mathrm{second} \\ $$$$\mathrm{question}\:\mathrm{is}\:\mathrm{false} \\ $$$$\left(\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{only}\:\mathrm{for}\:{m}\:=\:{n}\right. \\ $$$$\left.\mathrm{or}\:{m}\:=\:\frac{\mathrm{1}}{{n}}\right)\:\mathrm{but}\:: \\ $$$$\mathrm{log}_{{n}} {m}+\mathrm{log}_{\frac{\mathrm{1}}{{n}}} {m}\:= \\ $$$$\frac{\mathrm{ln}{m}}{\mathrm{ln}{n}}+\frac{\mathrm{ln}{m}}{\mathrm{ln}\frac{\mathrm{1}}{{n}}}\:=\: \\ $$$$\frac{\mathrm{ln}{m}}{\mathrm{ln}{n}}−\frac{\mathrm{ln}{m}}{\mathrm{ln}{n}}\:=\:\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com