
Question Number 104220 by bemath last updated on 20/Jul/20
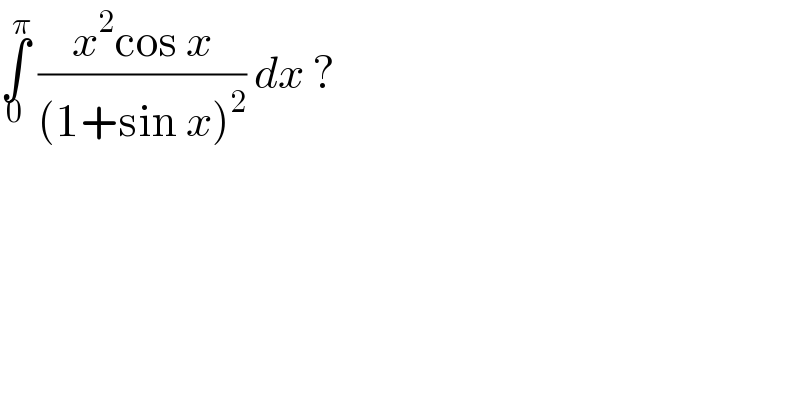
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{x}^{\mathrm{2}} \mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\:{dx}\:?\: \\ $$
Commented by bemath last updated on 20/Jul/20
$${thank}\:{you}\:{both}.\:{cooll} \\ $$
Answered by Ar Brandon last updated on 20/Jul/20
![I=∫_0 ^π ((x^2 cosx)/((1+sinx)^2 ))dx , x=π−u I=∫_0 ^π (((π−x)^2 cos(π−x))/((1+sin(π−x))^2 ))dx=−∫(((π−x)^2 cosx)/((1+sinx)^2 ))dx 2I=∫_0 ^π ((x^2 −(π^2 −2πx+x^2 ))/((1+sinx)^2 ))∙cosxdx=∫_0 ^π ((2πx−π^2 )/((1+sinx)^2 ))cosxdx =∫_0 ^π {((2πxcosx)/((1+sinx)^2 ))−((π^2 cosx)/((1+sinx)^2 ))}dx=∫_0 ^π ((2πxcosx)/((1+sinx)^2 ))dx+[(π^2 /(1+sinx))]_0 ^π u(x)=2πx⇒u′(x)=2π , v′(x)=((cosx)/((1+sinx)^2 ))⇒v(x)=((−1)/(1+sinx)) ⇒2I={((−2πx)/(1+sinx))+∫((2πdx)/(1+sinx))}_0 ^π ∫(dx/(1+sinx))=∫((1−sinx)/(cos^2 x))dx=tanx−secx ⇒2I=2π{((−x)/(1+sinx))+tanx−secx}_0 ^π =2π(2−π) ⇒∫_0 ^π ((x^2 cosx)/((1+sinx)^2 ))dx=(2−π)π](Q104222.png)
$$\mathcal{I}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{cosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\mathrm{dx}\:,\:\mathrm{x}=\pi−\mathrm{u} \\ $$$$\mathcal{I}=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−\mathrm{x}\right)^{\mathrm{2}} \mathrm{cos}\left(\pi−\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{sin}\left(\pi−\mathrm{x}\right)\right)^{\mathrm{2}} }\mathrm{dx}=−\int\frac{\left(\pi−\mathrm{x}\right)^{\mathrm{2}} \mathrm{cosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{2}\mathcal{I}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{x}^{\mathrm{2}} −\left(\pi^{\mathrm{2}} −\mathrm{2}\pi\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\centerdot\mathrm{cosxdx}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{2}\pi\mathrm{x}−\pi^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\mathrm{cosxdx} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \left\{\frac{\mathrm{2}\pi\mathrm{xcosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }−\frac{\pi^{\mathrm{2}} \mathrm{cosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\right\}\mathrm{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{2}\pi\mathrm{xcosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\mathrm{dx}+\left[\frac{\pi^{\mathrm{2}} }{\mathrm{1}+\mathrm{sinx}}\right]_{\mathrm{0}} ^{\pi} \\ $$$$\:\mathrm{u}\left(\mathrm{x}\right)=\mathrm{2}\pi\mathrm{x}\Rightarrow\mathrm{u}'\left(\mathrm{x}\right)=\mathrm{2}\pi\:,\:\mathrm{v}'\left(\mathrm{x}\right)=\frac{\mathrm{cosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\Rightarrow\mathrm{v}\left(\mathrm{x}\right)=\frac{−\mathrm{1}}{\mathrm{1}+\mathrm{sinx}} \\ $$$$\Rightarrow\mathrm{2}\mathcal{I}=\left\{\frac{−\mathrm{2}\pi\mathrm{x}}{\mathrm{1}+\mathrm{sinx}}+\int\frac{\mathrm{2}\pi\mathrm{dx}}{\mathrm{1}+\mathrm{sinx}}\right\}_{\mathrm{0}} ^{\pi} \\ $$$$\int\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{sinx}}=\int\frac{\mathrm{1}−\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}=\mathrm{tanx}−\mathrm{secx} \\ $$$$\Rightarrow\mathrm{2}\mathcal{I}=\mathrm{2}\pi\left\{\frac{−\mathrm{x}}{\mathrm{1}+\mathrm{sinx}}+\mathrm{tanx}−\mathrm{secx}\right\}_{\mathrm{0}} ^{\pi} =\mathrm{2}\pi\left(\mathrm{2}−\pi\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{cosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\mathrm{dx}=\left(\mathrm{2}−\pi\right)\pi \\ $$
Answered by john santu last updated on 20/Jul/20
![by parts { ((u=x^2 ⇒du=2x dx)),((v=∫ ((d(1+sin x))/((1+sin x)^2 )) =−(1/(1+sin x)) )) :} I= −(x^2 /(1+sin x)) ]_0 ^π +∫_0 ^π ((2x)/(1+sin x)) dx I= −π^2 +∫_0 ^π ((2x)/(1+sin x)) dx set J = ∫_0 ^π ((2x)/(1+sin x)) dx replace x by π−x J = ∫_π ^0 ((2(π−x))/(1+sin (π−x))) (−dx) J=∫_0 ^π ((2π−2x)/(1+sin x)) dx , so we have 2J = ∫_0 ^π ((2π)/(1+sin x)) dx ⇒J = ∫_0 ^π (π/(1+sin x))dx substitute t=x−(π/2) J=∫_0 ^(π/2) π sec^2 ((t/2)) dt = 2π hence we conclude that = −π^2 +2π (JS ⊛)](Q104226.png)
$${by}\:{parts} \\ $$$$\begin{cases}{{u}={x}^{\mathrm{2}} \Rightarrow{du}=\mathrm{2}{x}\:{dx}}\\{{v}=\int\:\frac{{d}\left(\mathrm{1}+\mathrm{sin}\:{x}\right)}{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}}\:}\end{cases} \\ $$$$\left.{I}=\:−\frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{sin}\:{x}}\:\right]_{\mathrm{0}} ^{\pi} \:+\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{2}{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx} \\ $$$${I}=\:−\pi^{\mathrm{2}} +\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{2}{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx}\: \\ $$$${set}\:{J}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{2}{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx} \\ $$$${replace}\:{x}\:{by}\:\pi−{x}\: \\ $$$${J}\:=\:\underset{\pi} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{2}\left(\pi−{x}\right)}{\mathrm{1}+\mathrm{sin}\:\left(\pi−{x}\right)}\:\left(−{dx}\right) \\ $$$${J}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{2}\pi−\mathrm{2}{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx}\:,\:{so}\:{we}\:{have} \\ $$$$\mathrm{2}{J}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{2}\pi}{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx}\:\Rightarrow{J}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\pi}{\mathrm{1}+\mathrm{sin}\:{x}}{dx} \\ $$$${substitute}\:{t}={x}−\frac{\pi}{\mathrm{2}} \\ $$$${J}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\pi\:\mathrm{sec}\:^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\:{dt}\:=\:\mathrm{2}\pi \\ $$$${hence}\:{we}\:{conclude}\:{that}\: \\ $$$$=\:−\pi^{\mathrm{2}} +\mathrm{2}\pi\:\:\left({JS}\:\circledast\right)\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 20/Jul/20
![I =∫_0 ^π ((x^2 cosx)/((1+sinx)^2 ))dx changement x =π−t give I =−∫_0 ^π (((π−t)^2 (cos(π−t)))/((1+sint)^2 ))(−dt) =−∫_0 ^π (((π^2 −2πt +t^2 )cost)/((1+sint)^2 ))dt =−π^2 ∫_0 ^π ((cost)/((1+sint)^2 )) +2π ∫_0 ^π ((tcost)/((1+sint)^2 ))dt −∫_0 ^π ((t^2 cost)/((1+sint)^2 ))dt ⇒ 2I =π^2 [(1/(1+sint))]_0 ^π +2π ∫_0 ^π ((tcost)/((1+sint)^2 ))dt =0 +2π ∫_0 ^(π ) ((tcost)/((1+sint)^2 ))dx by parts u^′ =((cost)/((1+sint)^2 )) and v =t ⇒ ∫_0 ^π ((tcost)/((1+sint)^2 ))dt =[−(t/(1+sint))]_0 ^π −∫_0 ^π −(1/(1+sint))dt =−π +∫_0 ^π (dt/(1+sint)) changement tan((t/2))=u give ∫_0 ^π (dt/(1+sint)) =∫_0 ^∞ ((2du)/((1+u^2 )(1+((2u)/(1+u^2 ))))) =∫_0 ^∞ ((2du)/(1+u^2 +2u)) =∫_0 ^∞ ((2du)/((u+1)^2 )) =[((−2)/(u+1))]_0 ^∞ =2 ⇒2I =2π{−π +2} ⇒I =2π−π^2](Q104257.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{cosx}}{\left(\mathrm{1}+\mathrm{sinx}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}\:=\pi−\mathrm{t}\:\mathrm{give}\: \\ $$$$\mathrm{I}\:=−\int_{\mathrm{0}} ^{\pi} \:\frac{\left(\pi−\mathrm{t}\right)^{\mathrm{2}} \left(\mathrm{cos}\left(\pi−\mathrm{t}\right)\right)}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\left(−\mathrm{dt}\right)\:=−\int_{\mathrm{0}} ^{\pi} \:\:\frac{\left(\pi^{\mathrm{2}} −\mathrm{2}\pi\mathrm{t}\:+\mathrm{t}^{\mathrm{2}} \right)\mathrm{cost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=−\pi^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\:+\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{tcost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\mathrm{dt}\:−\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{t}^{\mathrm{2}} \:\mathrm{cost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{2I}\:=\pi^{\mathrm{2}} \left[\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sint}}\right]_{\mathrm{0}} ^{\pi} \:+\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{tcost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{0}\:+\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\pi\:} \:\frac{\mathrm{tcost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\frac{\mathrm{cost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{v}\:=\mathrm{t}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{tcost}}{\left(\mathrm{1}+\mathrm{sint}\right)^{\mathrm{2}} }\mathrm{dt}\:=\left[−\frac{\mathrm{t}}{\mathrm{1}+\mathrm{sint}}\right]_{\mathrm{0}} ^{\pi} \:−\int_{\mathrm{0}} ^{\pi} \:−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sint}}\mathrm{dt} \\ $$$$=−\pi\:\:+\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{sint}}\:\:\mathrm{changement}\:\:\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}\:\mathrm{give} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{sint}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} +\mathrm{2u}}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2du}}{\left(\mathrm{u}+\mathrm{1}\right)^{\mathrm{2}} }\:=\left[\frac{−\mathrm{2}}{\mathrm{u}+\mathrm{1}}\right]_{\mathrm{0}} ^{\infty} =\mathrm{2} \\ $$$$\Rightarrow\mathrm{2I}\:=\mathrm{2}\pi\left\{−\pi\:+\mathrm{2}\right\}\:\Rightarrow\mathrm{I}\:=\mathrm{2}\pi−\pi^{\mathrm{2}} \\ $$$$ \\ $$
