Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104243 by  M±th+et+s last updated on 20/Jul/20

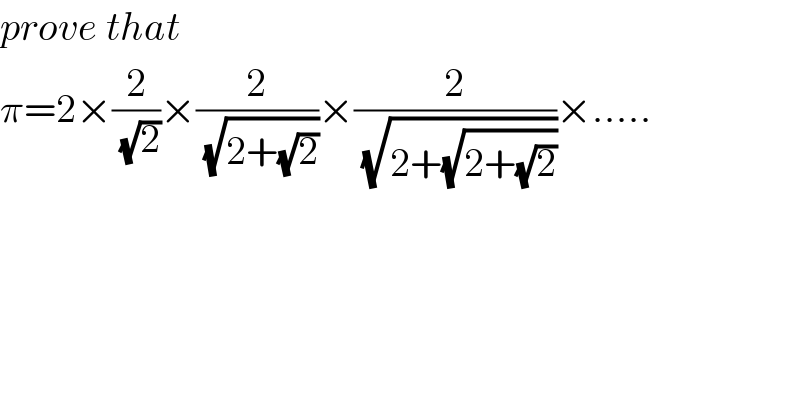
prove that π=2×(2/(√2))×(2/(√(2+(√2))))×(2/(√(2+(√(2+(√2))))))×.....

$${prove}\:{that} \\ $$$$\pi=\mathrm{2}×\frac{\mathrm{2}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{2}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}×\frac{\mathrm{2}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}×..... \\ $$

Answered by OlafThorendsen last updated on 20/Jul/20

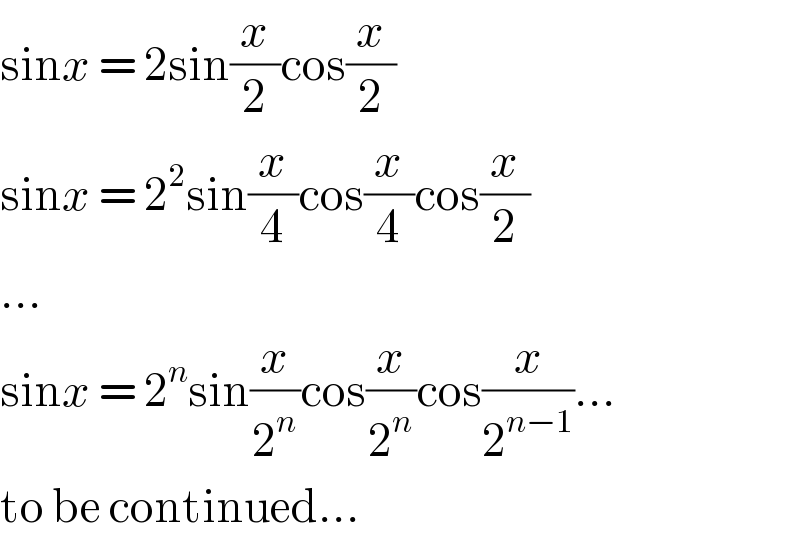
sinx = 2sin(x/2)cos(x/2) sinx = 2^2 sin(x/4)cos(x/4)cos(x/2) ... sinx = 2^n sin(x/2^n )cos(x/2^n )cos(x/2^(n−1) )... to be continued...

$$\mathrm{sin}{x}\:=\:\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{sin}{x}\:=\:\mathrm{2}^{\mathrm{2}} \mathrm{sin}\frac{{x}}{\mathrm{4}}\mathrm{cos}\frac{{x}}{\mathrm{4}}\mathrm{cos}\frac{{x}}{\mathrm{2}} \\ $$$$... \\ $$$$\mathrm{sin}{x}\:=\:\mathrm{2}^{{n}} \mathrm{sin}\frac{{x}}{\mathrm{2}^{{n}} }\mathrm{cos}\frac{{x}}{\mathrm{2}^{{n}} }\mathrm{cos}\frac{{x}}{\mathrm{2}^{{n}−\mathrm{1}} }... \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{continued}... \\ $$

Answered by Dwaipayan Shikari last updated on 20/Jul/20

2.(2/(√2)).(2/(√(2+(√2)))).(2/(√(2+(√(2+(√2))))))...... lim_(n→∞) S_n =2^n ((1/(√2)).(1/(√(2+(√2)))).(1/(√(2+(√(2+(√2))))))......n) S_n =2^n cos(π/4).(1/(2cos(π/8)2)).(1/(cos(π/(16))2)).(1/(cos(π/(32)))).....n S_n =2^n cos(π/4).(1/2^n )((1/(cos(0)........cos(π/8)))) S_n =cos(π/4).((1/(cos(π/8))).(1/(cos(π/(16)))).(1/(cos(π/(32))))....)continue

$$\mathrm{2}.\frac{\mathrm{2}}{\sqrt{\mathrm{2}}}.\frac{\mathrm{2}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}.\frac{\mathrm{2}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}...... \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\:\mathrm{S}_{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}.\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}.\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}......\mathrm{n}\right) \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \mathrm{cos}\frac{\pi}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2cos}\frac{\pi}{\mathrm{8}}\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{16}}\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{32}}}.....\mathrm{n} \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \mathrm{cos}\frac{\pi}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\left(\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{0}\right)........\mathrm{cos}\frac{\pi}{\mathrm{8}}}\right) \\ $$$$ \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{cos}\frac{\pi}{\mathrm{4}}.\left(\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{8}}}.\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{16}}}.\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{32}}}....\right)\mathrm{continue} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com