
Question Number 104264 by mohammad17 last updated on 20/Jul/20
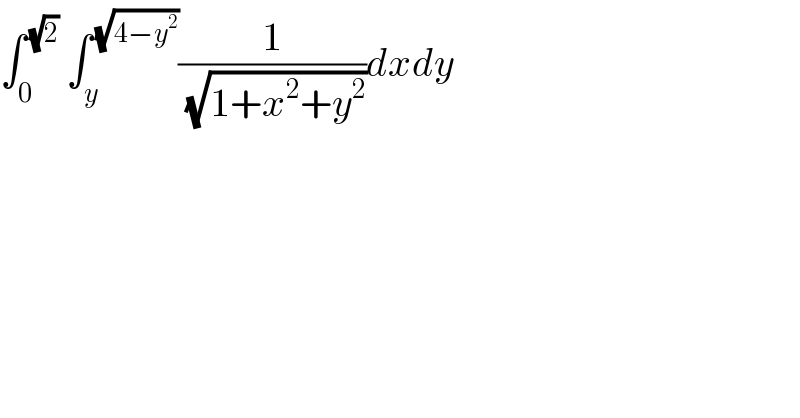
$$\int_{\mathrm{0}} ^{\:\sqrt{\mathrm{2}}} \:\int_{{y}} ^{\:\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }} \frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{dxdy} \\ $$
Answered by Ar Brandon last updated on 20/Jul/20

$$\mathcal{I}=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \left\{\int_{\mathrm{y}} ^{\sqrt{\mathrm{4}−\mathrm{y}^{\mathrm{2}} }} \frac{\mathrm{dx}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }}\right\}\mathrm{dy}=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}\centerdot\left\{\int_{\mathrm{y}} ^{\sqrt{\mathrm{4}−\mathrm{y}^{\mathrm{2}} }} \frac{\mathrm{dx}}{\sqrt{\mathrm{1}+\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}\right)^{\mathrm{2}} }}\right\}\mathrm{dy} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}\centerdot\frac{\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}{\mathrm{1}}\left\{\mathrm{Arcsinh}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}\right)\right\}_{\mathrm{y}} ^{\sqrt{\mathrm{4}−\mathrm{y}^{\mathrm{2}} }} \mathrm{dy} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \left\{\mathrm{Arcsinh}\left(\sqrt{\frac{\mathrm{4}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}\right)−\mathrm{Arcsinh}\left(\frac{\mathrm{y}}{\sqrt{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}\right)\right\}\mathrm{dy} \\ $$$${To}\:{be}\:{continued}... \\ $$
Commented by mohammad17 last updated on 20/Jul/20

$${sir}\:{by}\:{polar} \\ $$
Answered by Ar Brandon last updated on 21/Jul/20
![En coordonne^� es polaires x=rcosθ , y=rsinθ 0≤y≤(√2) ⇒0≤rsinθ≤(√2) ⇒0≤r≤((√2)/(sinθ)) y≤x≤(√(4−y^2 )) ⇒ { ((y≤x )),((x≤(√(4−y^2 )))) :}⇒ { ((tanθ≤1)),((x^2 +y^2 ≤4)) :}⇒ { ((θ≤(π/4))),((r≤2)) :} r=2⇒0≤2sinθ≤(√2) ⇒0≤θ≤(π/4) ⇒I=∫_0 ^(π/4) ∫_0 ^((√2)/(sinθ)) (r/(√(1+r^2 )))drdθ=∫_0 ^(π/4) [(√(1+r^2 ))]_0 ^((√2)/(sinθ)) dθ ⇒I=∫_0 ^(π/4) {(√(1+(2/(sin^2 θ))))−1}dθ=∫_0 ^(π/4) {(√(1+(2/(sin^2 θ))))}dθ−(π/4) A^� suivre...](Q104344.png)
$$ \\ $$$$\mathrm{En}\:\mathrm{coordonn}\acute {\mathrm{e}es}\:\mathrm{polaires}\:\mathrm{x}=\mathrm{rcos}\theta\:,\:\mathrm{y}=\mathrm{rsin}\theta \\ $$$$\mathrm{0}\leqslant\mathrm{y}\leqslant\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{0}\leqslant\mathrm{rsin}\theta\leqslant\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{0}\leqslant\mathrm{r}\leqslant\frac{\sqrt{\mathrm{2}}}{\mathrm{sin}\theta} \\ $$$$\mathrm{y}\leqslant\mathrm{x}\leqslant\sqrt{\mathrm{4}−\mathrm{y}^{\mathrm{2}} }\:\Rightarrow\begin{cases}{\mathrm{y}\leqslant\mathrm{x}\:}\\{\mathrm{x}\leqslant\sqrt{\mathrm{4}−\mathrm{y}^{\mathrm{2}} }}\end{cases}\Rightarrow\begin{cases}{\mathrm{tan}\theta\leqslant\mathrm{1}}\\{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{4}}\end{cases}\Rightarrow\begin{cases}{\theta\leqslant\frac{\pi}{\mathrm{4}}}\\{\mathrm{r}\leqslant\mathrm{2}}\end{cases} \\ $$$$\mathrm{r}=\mathrm{2}\Rightarrow\mathrm{0}\leqslant\mathrm{2sin}\theta\leqslant\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\mathrm{sin}\theta}} \frac{\mathrm{r}}{\sqrt{\mathrm{1}+\mathrm{r}^{\mathrm{2}} }}\mathrm{drd}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left[\sqrt{\mathrm{1}+\mathrm{r}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\mathrm{sin}\theta}} \mathrm{d}\theta \\ $$$$\Rightarrow\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{sin}^{\mathrm{2}} \theta}}−\mathrm{1}\right\}\mathrm{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{sin}^{\mathrm{2}} \theta}}\right\}\mathrm{d}\theta−\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\grave {\mathrm{A}}\:\mathrm{suivre}... \\ $$
Commented by Ar Brandon last updated on 21/Jul/20

$$ \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\sqrt{\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{2}}}{\mathrm{sin}\theta}\mathrm{d}\theta\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sin}\theta\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{sin}^{\mathrm{2}} \theta}}}{\mathrm{sin}\theta}\mathrm{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta}}\mathrm{d}\theta \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta}\:\Rightarrow\mathrm{cos}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\:\Rightarrow\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta} \\ $$$$=\frac{\mathrm{tan}^{\mathrm{2}} \theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\:\Rightarrow\frac{\mathrm{2}}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \theta}\:=\mathrm{2}×\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}{\mathrm{tan}^{\mathrm{2}} \theta}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\frac{\mathrm{2}+\mathrm{2tan}^{\mathrm{2}} \theta}{\mathrm{tan}^{\mathrm{2}} \theta}}\mathrm{d}\theta\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\frac{\mathrm{3tan}^{\mathrm{2}} \theta+\mathrm{2}}{\mathrm{tan}^{\mathrm{2}} \theta}}\mathrm{d}\theta\:\:=_{\mathrm{tan}\theta\:=\mathrm{x}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{3x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }}\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{3x}^{\mathrm{2}} +\mathrm{2}}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}\:\:=\sqrt{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{2}}{\mathrm{3}}}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx} \\ $$$$\mathrm{cha7gement}\:\mathrm{x}\:=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\mathrm{shu}\:\mathrm{give}\:\mathrm{u}\:=\mathrm{argsh}\left(\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\mathrm{x}\right) \\ $$$$\mathrm{I}\:=\sqrt{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{arhsh}\left(\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)} \:\:\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{chu}}{\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\mathrm{sh}\left(\mathrm{u}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sh}^{\mathrm{2}} \mathrm{u}\right)}×\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\mathrm{ch}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{ln}\left(\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}+\sqrt{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{4}}}\right)} \:\:\:\frac{\mathrm{ch}^{\mathrm{2}} \mathrm{u}}{\mathrm{shu}\left(\mathrm{3}+\mathrm{2sh}^{\mathrm{2}} \mathrm{u}\right)}\mathrm{du}\:\:\:\:\mathrm{and}\:\mathrm{this}\:\mathrm{integral}\:\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved} \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 21/Jul/20
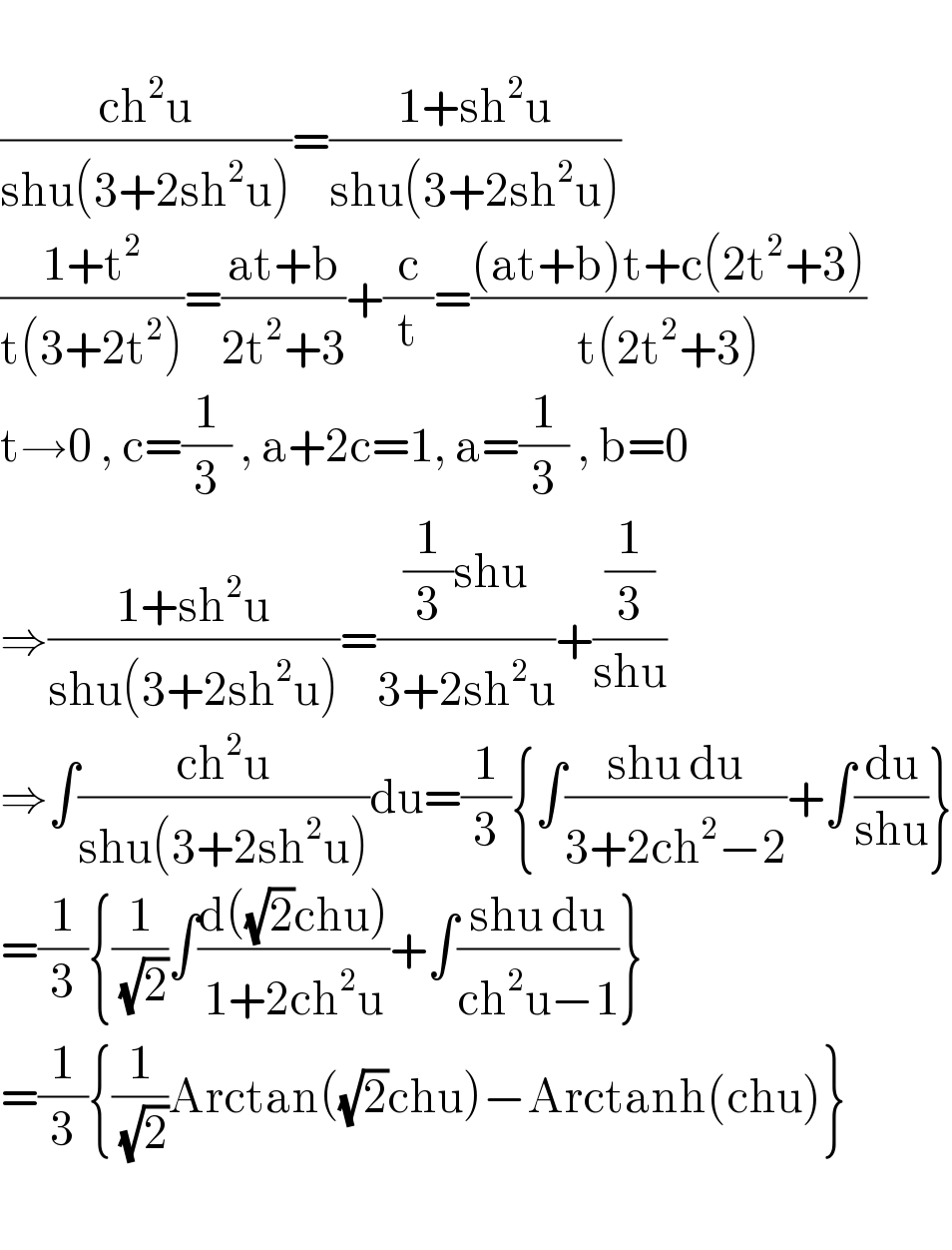
$$ \\ $$$$\frac{\mathrm{ch}^{\mathrm{2}} \mathrm{u}}{\mathrm{shu}\left(\mathrm{3}+\mathrm{2sh}^{\mathrm{2}} \mathrm{u}\right)}=\frac{\mathrm{1}+\mathrm{sh}^{\mathrm{2}} \mathrm{u}}{\mathrm{shu}\left(\mathrm{3}+\mathrm{2sh}^{\mathrm{2}} \mathrm{u}\right)} \\ $$$$\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{t}\left(\mathrm{3}+\mathrm{2t}^{\mathrm{2}} \right)}=\frac{\mathrm{at}+\mathrm{b}}{\mathrm{2t}^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{c}}{\mathrm{t}}=\frac{\left(\mathrm{at}+\mathrm{b}\right)\mathrm{t}+\mathrm{c}\left(\mathrm{2t}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{t}\left(\mathrm{2t}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$$$\mathrm{t}\rightarrow\mathrm{0}\:,\:\mathrm{c}=\frac{\mathrm{1}}{\mathrm{3}}\:,\:\mathrm{a}+\mathrm{2c}=\mathrm{1},\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{3}}\:,\:\mathrm{b}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}+\mathrm{sh}^{\mathrm{2}} \mathrm{u}}{\mathrm{shu}\left(\mathrm{3}+\mathrm{2sh}^{\mathrm{2}} \mathrm{u}\right)}=\frac{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{shu}}{\mathrm{3}+\mathrm{2sh}^{\mathrm{2}} \mathrm{u}}+\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{shu}} \\ $$$$\Rightarrow\int\frac{\mathrm{ch}^{\mathrm{2}} \mathrm{u}}{\mathrm{shu}\left(\mathrm{3}+\mathrm{2sh}^{\mathrm{2}} \mathrm{u}\right)}\mathrm{du}=\frac{\mathrm{1}}{\mathrm{3}}\left\{\int\frac{\mathrm{shu}\:\mathrm{du}}{\mathrm{3}+\mathrm{2ch}^{\mathrm{2}} −\mathrm{2}}+\int\frac{\mathrm{du}}{\mathrm{shu}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\int\frac{\mathrm{d}\left(\sqrt{\mathrm{2}}\mathrm{chu}\right)}{\mathrm{1}+\mathrm{2ch}^{\mathrm{2}} \mathrm{u}}+\int\frac{\mathrm{shu}\:\mathrm{du}}{\mathrm{ch}^{\mathrm{2}} \mathrm{u}−\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{Arctan}\left(\sqrt{\mathrm{2}}\mathrm{chu}\right)−\mathrm{Arctanh}\left(\mathrm{chu}\right)\right\} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 21/Jul/20
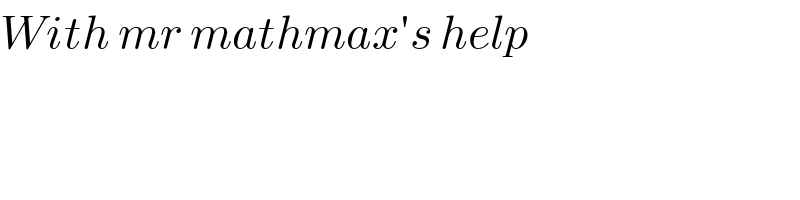
$${With}\:{mr}\:{mathmax}'{s}\:{help} \\ $$
