Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104413 by Anindita last updated on 21/Jul/20

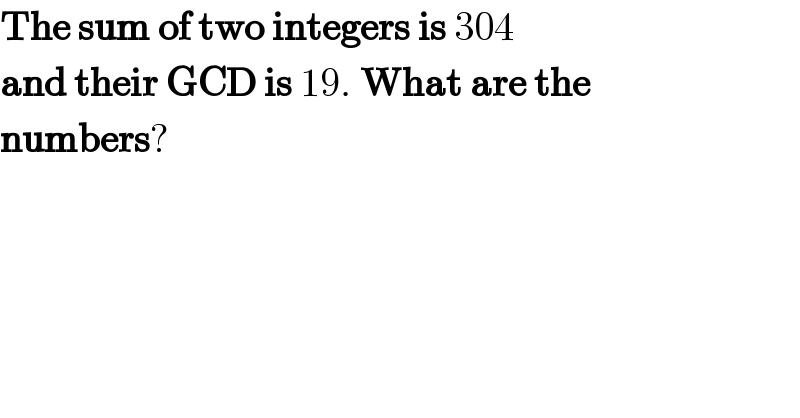
The sum of two integers is 304 and their GCD is 19. What are the numbers?

$$\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{two}}\:\boldsymbol{\mathrm{integers}}\:\boldsymbol{\mathrm{is}}\:\mathrm{304} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{their}}\:\boldsymbol{\mathrm{GCD}}\:\boldsymbol{\mathrm{is}}\:\mathrm{19}.\:\boldsymbol{\mathrm{What}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{numbers}}? \\ $$

Answered by Rasheed.Sindhi last updated on 22/Jul/20

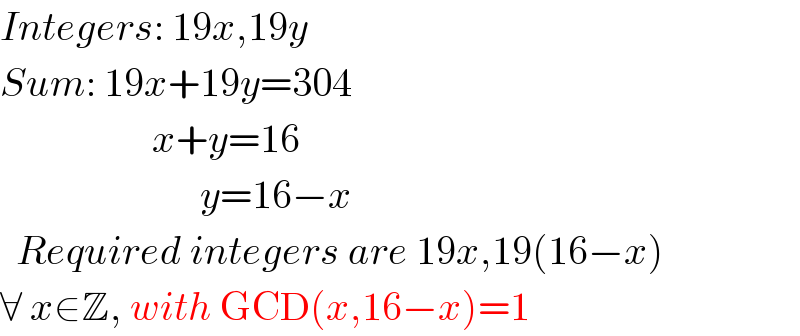
Integers: 19x,19y Sum: 19x+19y=304 x+y=16 y=16−x Required integers are 19x,19(16−x) ∀ x∈Z, with GCD(x,16−x)=1

$${Integers}:\:\mathrm{19}{x},\mathrm{19}{y} \\ $$$${Sum}:\:\mathrm{19}{x}+\mathrm{19}{y}=\mathrm{304} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}+{y}=\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{16}−{x} \\ $$$$\:\:{Required}\:{integers}\:{are}\:\mathrm{19}{x},\mathrm{19}\left(\mathrm{16}−{x}\right) \\ $$$$\forall\:{x}\in\mathbb{Z},\:{with}\:\mathrm{GCD}\left({x},\mathrm{16}−{x}\right)=\mathrm{1} \\ $$

Commented by floor(10²Eta[1]) last updated on 21/Jul/20

you are including all the cases when gcd(x, y)≠1 which is not correct

$$\mathrm{you}\:\mathrm{are}\:\mathrm{including}\:\mathrm{all}\:\mathrm{the}\:\mathrm{cases}\:\mathrm{when} \\ $$$$\mathrm{gcd}\left(\mathrm{x},\:\mathrm{y}\right)\neq\mathrm{1}\:\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct} \\ $$

Commented by Rasheed.Sindhi last updated on 22/Jul/20

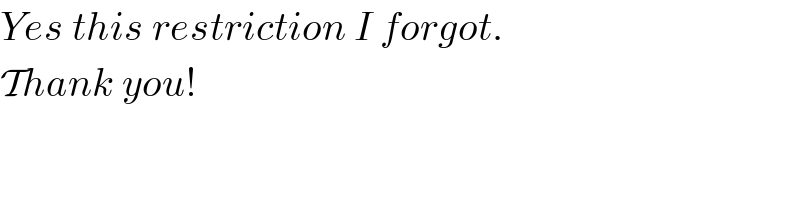
Yes this restriction I forgot. Thank you!

$${Yes}\:{this}\:{restriction}\:{I}\:{forgot}. \\ $$$$\mathcal{T}{hank}\:{you}! \\ $$

Answered by 1549442205PVT last updated on 21/Jul/20

Since GCD(a,b)=19 ⇒ { ((a=19m)),((b=19n)) :} where gcd(m,n)=1 From the hypothesis a+b=304 we get 19(m+n)=304⇒m+n=16. WLOG we suppose m<n.Then we have the following cases: (note that gcd(m,n)=1⇒m is odd) i)m=1⇒n=15⇒(a,b)=(19,285) ii)m=3⇒n=13⇒(a,b)=(57,247) iii)m=5⇒n=11⇒(a,b)=(209,95) iv)m=7⇒n=9⇒(a,b)=(153,151) Thus all the pairs (a,b) of positive integers which we need to find as: (a,b)∈{(19;285),(57,247),(209;95),(153;151)} and the permutations of them

$$\mathrm{Since}\:\mathrm{GCD}\left(\mathrm{a},\mathrm{b}\right)=\mathrm{19}\:\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{19m}}\\{\mathrm{b}=\mathrm{19n}}\end{cases} \\ $$$$\mathrm{where}\:\mathrm{gcd}\left(\mathrm{m},\mathrm{n}\right)=\mathrm{1} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{a}+\mathrm{b}=\mathrm{304}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{19}\left(\mathrm{m}+\mathrm{n}\right)=\mathrm{304}\Rightarrow\mathrm{m}+\mathrm{n}=\mathrm{16}. \\ $$$$\mathrm{WLOG}\:\mathrm{we}\:\mathrm{suppose}\:\mathrm{m}<\mathrm{n}.\mathrm{Then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{the}\:\mathrm{following}\:\mathrm{cases}: \\ $$$$\left(\mathrm{note}\:\mathrm{that}\:\mathrm{gcd}\left(\mathrm{m},\mathrm{n}\right)=\mathrm{1}\Rightarrow\mathrm{m}\:\mathrm{is}\:\mathrm{odd}\right) \\ $$$$\left.\mathrm{i}\right)\mathrm{m}=\mathrm{1}\Rightarrow\mathrm{n}=\mathrm{15}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{19},\mathrm{285}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{m}=\mathrm{3}\Rightarrow\mathrm{n}=\mathrm{13}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{57},\mathrm{247}\right) \\ $$$$\left.\mathrm{iii}\right)\mathrm{m}=\mathrm{5}\Rightarrow\mathrm{n}=\mathrm{11}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{209},\mathrm{95}\right) \\ $$$$\left.\mathrm{iv}\right)\mathrm{m}=\mathrm{7}\Rightarrow\mathrm{n}=\mathrm{9}\Rightarrow\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{153},\mathrm{151}\right) \\ $$$$\mathrm{Thus}\:\mathrm{all}\:\mathrm{the}\:\mathrm{pairs}\:\left(\mathrm{a},\mathrm{b}\right)\:\mathrm{of}\:\mathrm{positive} \\ $$$$\mathrm{integers}\:\mathrm{which}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find}\:\mathrm{as}: \\ $$$$\left(\mathrm{a},\mathrm{b}\right)\in\left\{\left(\mathrm{19};\mathrm{285}\right),\left(\mathrm{57},\mathrm{247}\right),\left(\mathrm{209};\mathrm{95}\right),\left(\mathrm{153};\mathrm{151}\right)\right\} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{permutations}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{them}} \\ $$$$ \\ $$

Commented by floor(10²Eta[1]) last updated on 21/Jul/20

gcd(153,151)=1≠19. the last case should be (a,b)=(133,171)

$$\mathrm{gcd}\left(\mathrm{153},\mathrm{151}\right)=\mathrm{1}\neq\mathrm{19}. \\ $$$$\mathrm{the}\:\mathrm{last}\:\mathrm{case}\:\mathrm{should}\:\mathrm{be} \\ $$$$\left(\mathrm{a},\mathrm{b}\right)=\left(\mathrm{133},\mathrm{171}\right) \\ $$

Commented by floor(10²Eta[1]) last updated on 21/Jul/20

m=2s+1, n=2t+1 m+n=2s+2t+2=16⇒s+t=7 s=k, t=7−k m=2k+1, n=15−2k 2k+1<15−2k⇒k≤3 so all the pairs (a, b) of integers are: (a, b)={19(2k+1), 19(15−2k)} ∀ k≤3

$$\mathrm{m}=\mathrm{2s}+\mathrm{1},\:\mathrm{n}=\mathrm{2t}+\mathrm{1} \\ $$$$\mathrm{m}+\mathrm{n}=\mathrm{2s}+\mathrm{2t}+\mathrm{2}=\mathrm{16}\Rightarrow\mathrm{s}+\mathrm{t}=\mathrm{7} \\ $$$$\mathrm{s}=\mathrm{k},\:\mathrm{t}=\mathrm{7}−\mathrm{k} \\ $$$$\mathrm{m}=\mathrm{2k}+\mathrm{1},\:\mathrm{n}=\mathrm{15}−\mathrm{2k} \\ $$$$\mathrm{2k}+\mathrm{1}<\mathrm{15}−\mathrm{2k}\Rightarrow\mathrm{k}\leqslant\mathrm{3} \\ $$$$\mathrm{so}\:\mathrm{all}\:\mathrm{the}\:\mathrm{pairs}\:\left(\mathrm{a},\:\mathrm{b}\right)\:\mathrm{of}\:\mathrm{integers}\:\mathrm{are}: \\ $$$$\left(\mathrm{a},\:\mathrm{b}\right)=\left\{\mathrm{19}\left(\mathrm{2k}+\mathrm{1}\right),\:\mathrm{19}\left(\mathrm{15}−\mathrm{2k}\right)\right\}\:\forall\:\mathrm{k}\leqslant\mathrm{3} \\ $$$$ \\ $$

Commented by 1549442205PVT last updated on 22/Jul/20

Thank you sir,i mistaked this case

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir},\mathrm{i}\:\mathrm{mistaked}\:\mathrm{this}\:\mathrm{case} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com