Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 104468 by ajfour last updated on 21/Jul/20

Commented by ajfour last updated on 21/Jul/20

Find r and hence area of △ABC in terms of R.

$${Find}\:{r}\:{and}\:{hence}\:{area}\:{of}\:\bigtriangleup{ABC}\:{in} \\ $$$${terms}\:{of}\:{R}. \\ $$

Commented by mr W last updated on 22/Jul/20

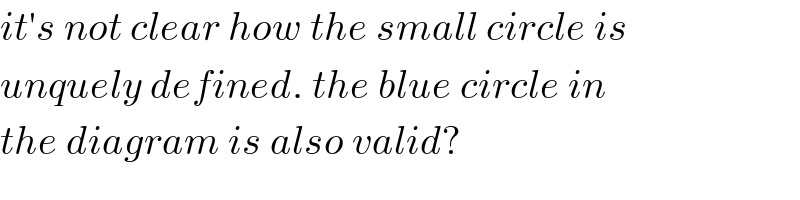
it′s not clear how the small circle is unquely defined. the blue circle in the diagram is also valid?

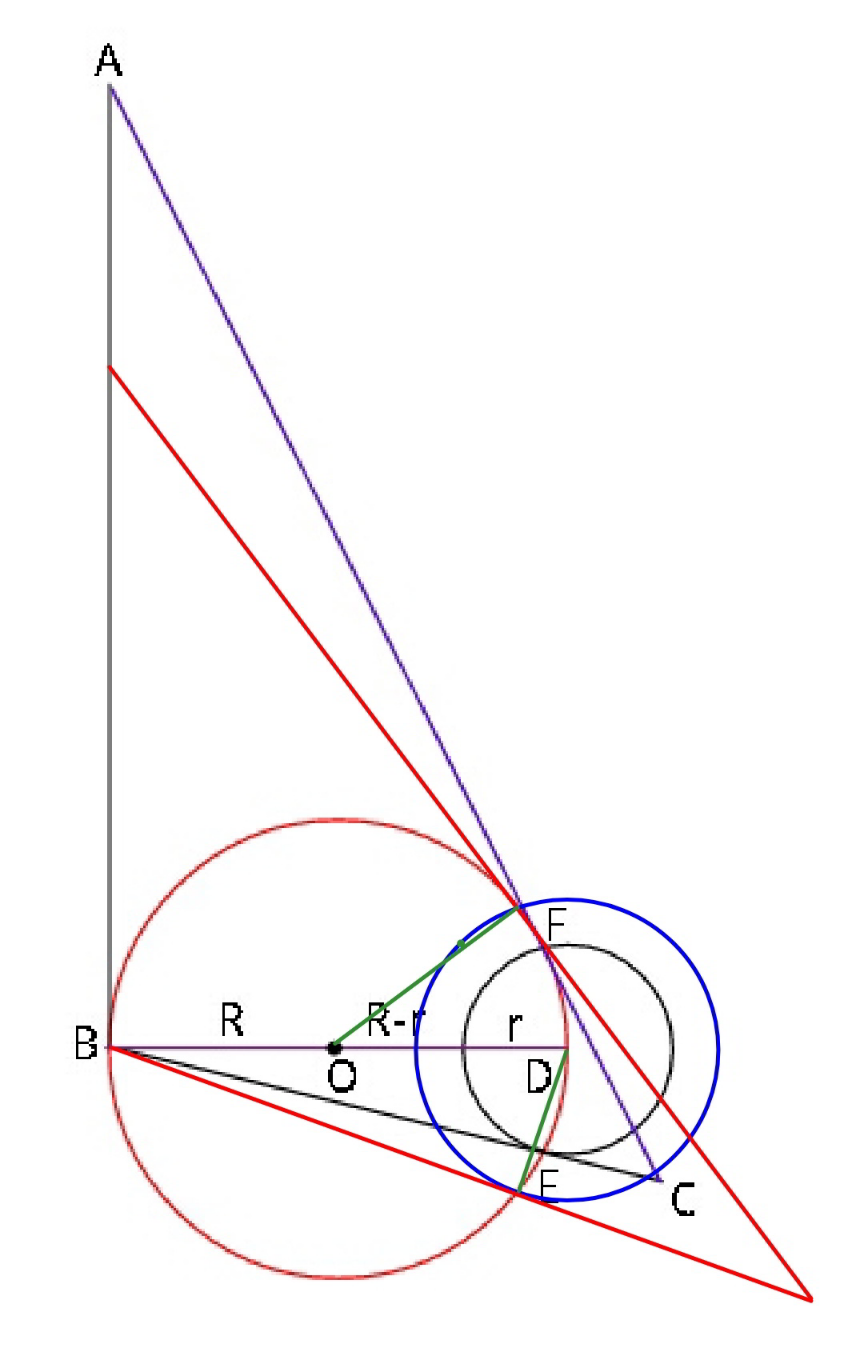
$${it}'{s}\:{not}\:{clear}\:{how}\:{the}\:{small}\:{circle}\:{is} \\ $$$${unquely}\:{defined}.\:{the}\:{blue}\:{circle}\:{in} \\ $$$${the}\:{diagram}\:{is}\:{also}\:{valid}? \\ $$

Commented by mr W last updated on 22/Jul/20

Commented by malwaan last updated on 22/Jul/20

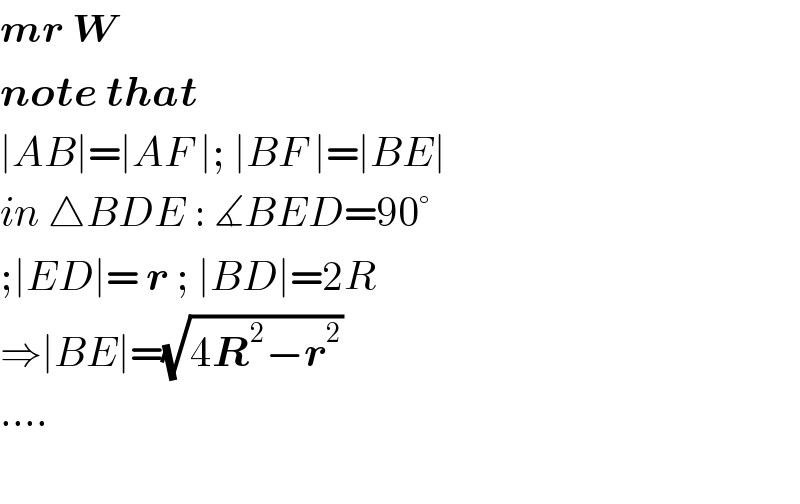
mr W note that ∣AB∣=∣AF ∣; ∣BF ∣=∣BE∣ in △BDE : ∡BED=90° ;∣ED∣= r ; ∣BD∣=2R ⇒∣BE∣=(√(4R^2 −r^2 )) ....

$$\boldsymbol{{mr}}\:\boldsymbol{{W}} \\ $$$$\boldsymbol{{note}}\:\boldsymbol{{that}} \\ $$$$\mid{AB}\mid=\mid{AF}\:\mid;\:\mid{BF}\:\mid=\mid{BE}\mid \\ $$$${in}\:\bigtriangleup{BDE}\::\:\measuredangle{BED}=\mathrm{90}° \\ $$$$;\mid{ED}\mid=\:\boldsymbol{{r}}\:;\:\mid{BD}\mid=\mathrm{2}{R} \\ $$$$\Rightarrow\mid{BE}\mid=\sqrt{\mathrm{4}\boldsymbol{{R}}^{\mathrm{2}} −\boldsymbol{{r}}^{\mathrm{2}} } \\ $$$$.... \\ $$$$ \\ $$

Commented by mr W last updated on 22/Jul/20

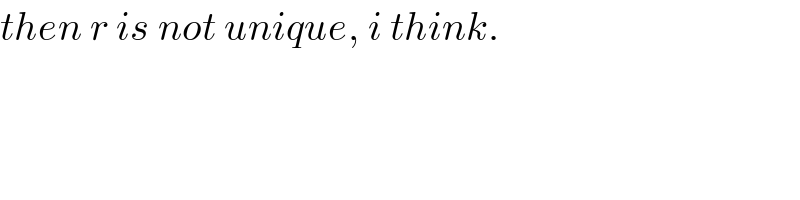
then r is not unique, i think.

$${then}\:{r}\:{is}\:{not}\:{unique},\:{i}\:{think}. \\ $$

Commented by ajfour last updated on 22/Jul/20

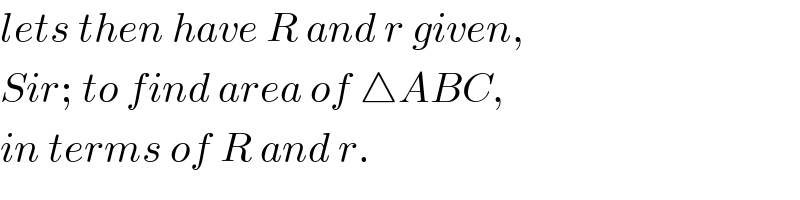
lets then have R and r given, Sir; to find area of △ABC, in terms of R and r.

$${lets}\:{then}\:{have}\:{R}\:{and}\:{r}\:{given}, \\ $$$${Sir};\:{to}\:{find}\:{area}\:{of}\:\bigtriangleup{ABC}, \\ $$$${in}\:{terms}\:{of}\:{R}\:{and}\:{r}. \\ $$

Commented by malwaan last updated on 22/Jul/20

it depend on the location of the point A SO you are absolutely right mr W

$${it}\:{depend}\:{on}\:{the}\:{location} \\ $$$${of}\:{the}\:{point}\:\boldsymbol{{A}} \\ $$$$\boldsymbol{{SO}}\:{you}\:{are}\:{absolutely}\:{right} \\ $$$${mr}\:{W} \\ $$

Answered by mr W last updated on 22/Jul/20

Commented by mr W last updated on 22/Jul/20

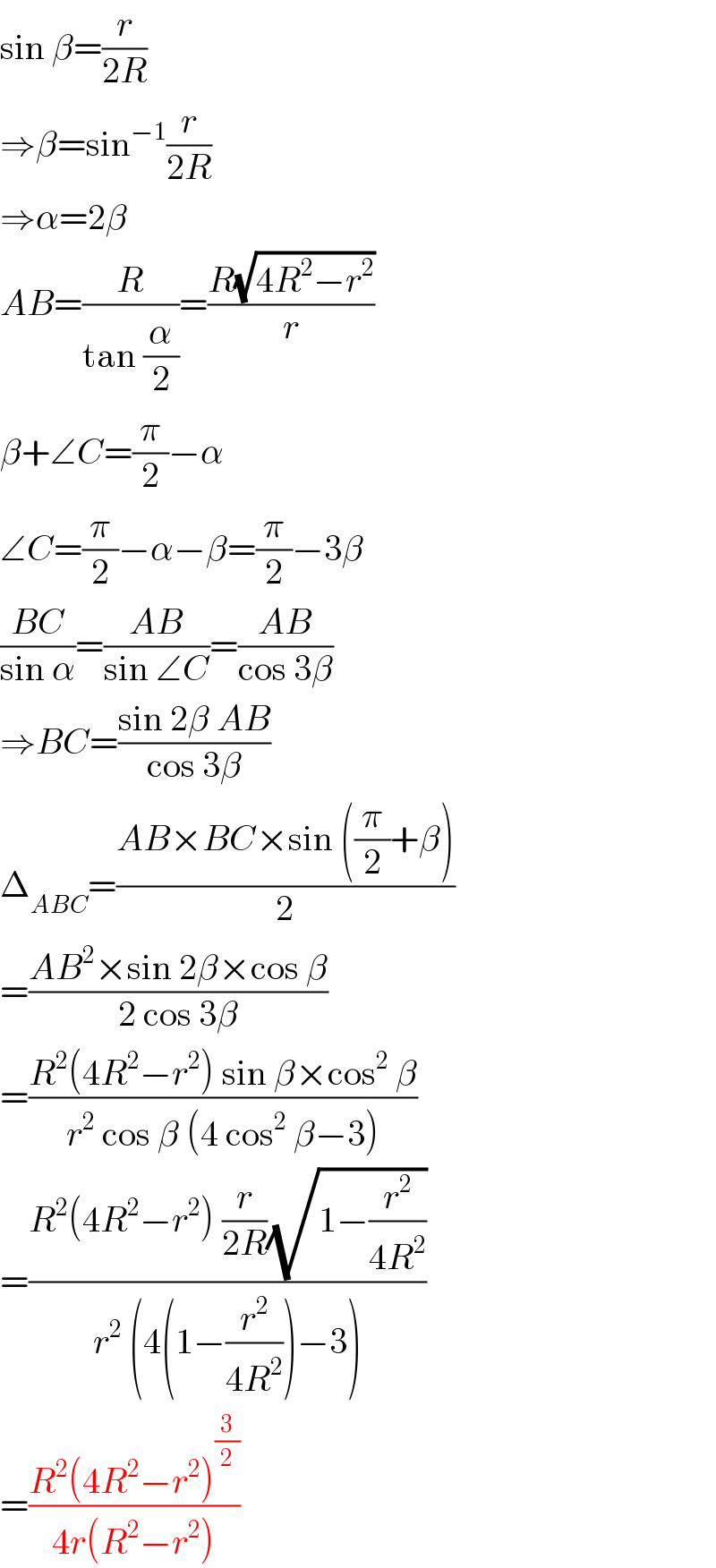
sin β=(r/(2R)) ⇒β=sin^(−1) (r/(2R)) ⇒α=2β AB=(R/(tan (α/2)))=((R(√(4R^2 −r^2 )))/r) β+∠C=(π/2)−α ∠C=(π/2)−α−β=(π/2)−3β ((BC)/(sin α))=((AB)/(sin ∠C))=((AB)/(cos 3β)) ⇒BC=((sin 2β AB)/(cos 3β)) Δ_(ABC) =((AB×BC×sin ((π/2)+β))/2) =((AB^2 ×sin 2β×cos β)/(2 cos 3β)) =((R^2 (4R^2 −r^2 ) sin β×cos^2 β)/(r^2 cos β (4 cos^2 β−3))) =((R^2 (4R^2 −r^2 ) (r/(2R))(√(1−(r^2 /(4R^2 )))))/(r^2 (4(1−(r^2 /(4R^2 )))−3))) =((R^2 (4R^2 −r^2 )^(3/2) )/(4r(R^2 −r^2 )))

$$\mathrm{sin}\:\beta=\frac{{r}}{\mathrm{2}{R}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{\mathrm{2}{R}} \\ $$$$\Rightarrow\alpha=\mathrm{2}\beta \\ $$$${AB}=\frac{{R}}{\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}=\frac{{R}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }}{{r}} \\ $$$$\beta+\angle{C}=\frac{\pi}{\mathrm{2}}−\alpha \\ $$$$\angle{C}=\frac{\pi}{\mathrm{2}}−\alpha−\beta=\frac{\pi}{\mathrm{2}}−\mathrm{3}\beta \\ $$$$\frac{{BC}}{\mathrm{sin}\:\alpha}=\frac{{AB}}{\mathrm{sin}\:\angle{C}}=\frac{{AB}}{\mathrm{cos}\:\mathrm{3}\beta} \\ $$$$\Rightarrow{BC}=\frac{\mathrm{sin}\:\mathrm{2}\beta\:{AB}}{\mathrm{cos}\:\mathrm{3}\beta} \\ $$$$\Delta_{{ABC}} =\frac{{AB}×{BC}×\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\beta\right)}{\mathrm{2}} \\ $$$$=\frac{{AB}^{\mathrm{2}} ×\mathrm{sin}\:\mathrm{2}\beta×\mathrm{cos}\:\beta}{\mathrm{2}\:\mathrm{cos}\:\mathrm{3}\beta} \\ $$$$=\frac{{R}^{\mathrm{2}} \left(\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)\:\mathrm{sin}\:\beta×\mathrm{cos}^{\mathrm{2}} \:\beta}{{r}^{\mathrm{2}} \:\mathrm{cos}\:\beta\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\beta−\mathrm{3}\right)} \\ $$$$=\frac{{R}^{\mathrm{2}} \left(\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)\:\frac{{r}}{\mathrm{2}{R}}\sqrt{\mathrm{1}−\frac{{r}^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }}}{{r}^{\mathrm{2}} \:\left(\mathrm{4}\left(\mathrm{1}−\frac{{r}^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }\right)−\mathrm{3}\right)} \\ $$$$=\frac{{R}^{\mathrm{2}} \left(\mathrm{4}{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{4}{r}\left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)} \\ $$

Commented by ajfour last updated on 24/Jul/20

thanks sir, shall review it, bit unwell again.. Elegant Solving Sir, too good to follow it even, thanks a lot!

$${thanks}\:{sir},\:{shall}\:{review}\:{it},\:{bit} \\ $$$${unwell}\:{again}.. \\ $$$${Elegant}\:{Solving}\:{Sir},\:{too}\:{good}\:{to} \\ $$$${follow}\:{it}\:{even},\:{thanks}\:{a}\:{lot}! \\ $$

Commented by mr W last updated on 23/Jul/20

get well!

$${get}\:{well}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com