Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 104505 by mathmax by abdo last updated on 22/Jul/20

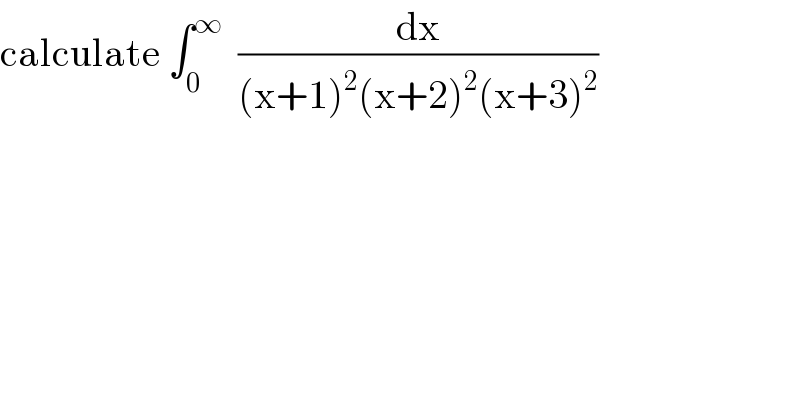
$$\mathrm{calculate}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{dx}}{{(\mathrm{x}+1)}^2{(\mathrm{x}+2)}^2{(\mathrm{x}+3)}^2}$$

Answered by OlafThorendsen last updated on 22/Jul/20

$$\mathrm{R}\left(x\right)=\frac{1}{{(\mathrm{x}+1)}^2{(\mathrm{x}+2)}^2{(\mathrm{x}+3)}^2}$$$$\mathrm{R}\left(x\right)=\frac{1}{4{(\mathrm{x}+1)}^2}+\frac{1}{{(\mathrm{x}+2)}^2}+\frac{1}{4{(\mathrm{x}+3)}^2}$$$$-\frac{3}{4(\mathrm{x}+1)}+\frac{3}{4(\mathrm{x}+3)}$$$${\int }_0^{\mathrm{\infty }}\mathrm{R}\left(\mathrm{x}\right)\mathrm{dx}=$$$${[-\frac{1}{4(\mathrm{x}+1)}-\frac{1}{\mathrm{x}+2}-\frac{1}{4(\mathrm{x}+3)}-\frac{3}{4}\ln \mid \frac{\mathrm{x}+1}{\mathrm{x}+3}\mid ]}_0^{\mathrm{\infty }}$$$$=\frac{1}{4}+\frac{1}{2}+\frac{1}{12}+\frac{3}{4}\ln \frac{1}{3}$$$$=\frac{5}{6}-\frac{3}{4}\ln 3$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com