Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104517 by Quvonchbek last updated on 22/Jul/20

Answered by 1549442205PVT last updated on 22/Jul/20

It is easy to see that the sequence of numbers: 11,19,29,41,...has general term is n^2 +3n+1(n∈N^∗ ).Hence, S=Σ_(n=1) ^(∞) ((n^2 +3n+1)/(n!))=Σ_(k=1) ^(∞) (n^2 /(n!))+Σ_(n=1) ^(∞) ((3n)/(n!))+Σ_(n=1) ^(∞) (1/(n!))(∗) On the other hands,we have e=Σ_(n=0) ^(∞) (1/(n!))=1+(1/(1!))+(1/(2!))+(1/(3!))+(1/(4!))+...Hence, Σ_(n=1) ^∞ ((3n)/(n!))=(3/(1!))+((3.2)/(2!))+((3.3)/(3!))+((3.4)/(4!))+... =3+(3/(1!))+(3/(2!))+(3/(3!))+...=3(1+(1/(1!))+(1/(2!))+(1/(3!))+...) =3e(1).Also we have also Σ_(n=1) ^∞ (1/(n!))=(1/(1!))+(1/(2!))+(1/(3!))+...=e−1(1) Σ_(n=1) ^∞ (n^2 /(n!))=(1/(1!))+(4/(2!))+(9/(3!))+((16)/(4!))+... =(1/(1!))+(2/(1!))+(3/(2!))+(4/(3!))+... We have also that e=1+(1/(1!))+(1/(2!))+(1/(3!))+(1/(4!))+... =1+((2−1)/(1!))+((3−2)/(2!))+((4−3)/(3!))+((5−4)/(4!))+... =(1/(1!))+(2/(1!))+(3/(2!))+(4/(3!))+(5/(4!))+...−(1+(1/(1!))+(1/(2!))+(1/(3!))+...) =1+(2/(1!))+(3/(2!))+(4/(3!))+(5/(4!))+...−e ⇒2e=(1/(1!))+(2/(1!))+(3/(2!))+(4/(3!))+(5/(4!))+...(2) From(∗), (1)and(2) we get S=Σ((n^2 +3n+1)/(n!))=e−1+3e+2e=6e−1 =ae^b +c⇒a=6,b=1,c=−1.Therefore, a+b+c=6

$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{numbers}: \\ $$$$\mathrm{11},\mathrm{19},\mathrm{29},\mathrm{41},...\mathrm{has}\:\mathrm{general}\:\mathrm{term}\:\mathrm{is} \\ $$$$\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1}\left(\mathrm{n}\in\mathbb{N}^{\ast} \right).\mathrm{Hence}, \\ $$$$\mathrm{S}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1}}{\mathrm{n}!}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}!}+\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{3n}}{\mathrm{n}!}+\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\frac{\mathrm{1}}{\mathrm{n}!}\left(\ast\right) \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands},\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{e}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\Sigma}}\frac{\mathrm{1}}{\mathrm{n}!}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+...\mathrm{Hence}, \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3n}}{\mathrm{n}!}=\frac{\mathrm{3}}{\mathrm{1}!}+\frac{\mathrm{3}.\mathrm{2}}{\mathrm{2}!}+\frac{\mathrm{3}.\mathrm{3}}{\mathrm{3}!}+\frac{\mathrm{3}.\mathrm{4}}{\mathrm{4}!}+... \\ $$$$=\mathrm{3}+\frac{\mathrm{3}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{3}}{\mathrm{3}!}+...=\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+...\right) \\ $$$$=\mathrm{3e}\left(\mathrm{1}\right).\mathrm{Also}\:\mathrm{we}\:\mathrm{have}\:\mathrm{also} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}!}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+...=\mathrm{e}−\mathrm{1}\left(\mathrm{1}\right) \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}!}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{4}}{\mathrm{2}!}+\frac{\mathrm{9}}{\mathrm{3}!}+\frac{\mathrm{16}}{\mathrm{4}!}+... \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+... \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{also}\:\mathrm{that} \\ $$$$\mathrm{e}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+... \\ $$$$=\mathrm{1}+\frac{\mathrm{2}−\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{3}−\mathrm{2}}{\mathrm{2}!}+\frac{\mathrm{4}−\mathrm{3}}{\mathrm{3}!}+\frac{\mathrm{5}−\mathrm{4}}{\mathrm{4}!}+... \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+\frac{\mathrm{5}}{\mathrm{4}!}+...−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+...\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+\frac{\mathrm{5}}{\mathrm{4}!}+...−\mathrm{e} \\ $$$$\Rightarrow\mathrm{2e}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{2}}{\mathrm{1}!}+\frac{\mathrm{3}}{\mathrm{2}!}+\frac{\mathrm{4}}{\mathrm{3}!}+\frac{\mathrm{5}}{\mathrm{4}!}+...\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\left(\ast\right),\:\left(\mathrm{1}\right)\mathrm{and}\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{S}=\Sigma\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{1}}{\mathrm{n}!}=\mathrm{e}−\mathrm{1}+\mathrm{3e}+\mathrm{2e}=\mathrm{6e}−\mathrm{1} \\ $$$$=\mathrm{ae}^{\mathrm{b}} +\mathrm{c}\Rightarrow\mathrm{a}=\mathrm{6},\mathrm{b}=\mathrm{1},\mathrm{c}=−\mathrm{1}.\mathrm{Therefore}, \\ $$$$\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}}=\mathrm{6} \\ $$

Commented by OlafThorendsen last updated on 22/Jul/20

The sum starts at 1, not at 0. Finally the good result is 6e−1 sir.

$$\mathrm{The}\:\mathrm{sum}\:\mathrm{starts}\:\mathrm{at}\:\mathrm{1},\:\mathrm{not}\:\mathrm{at}\:\mathrm{0}. \\ $$$$\mathrm{Finally}\:\mathrm{the}\:\mathrm{good}\:\mathrm{result}\:\mathrm{is}\:\mathrm{6e}−\mathrm{1}\:\mathrm{sir}. \\ $$

Commented by 1549442205PVT last updated on 22/Jul/20

Thank you Sir.I mistaked and corrected.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}.\mathrm{I}\:\mathrm{mistaked}\:\mathrm{and} \\ $$$$\mathrm{corrected}. \\ $$

Answered by OlafThorendsen last updated on 22/Jul/20

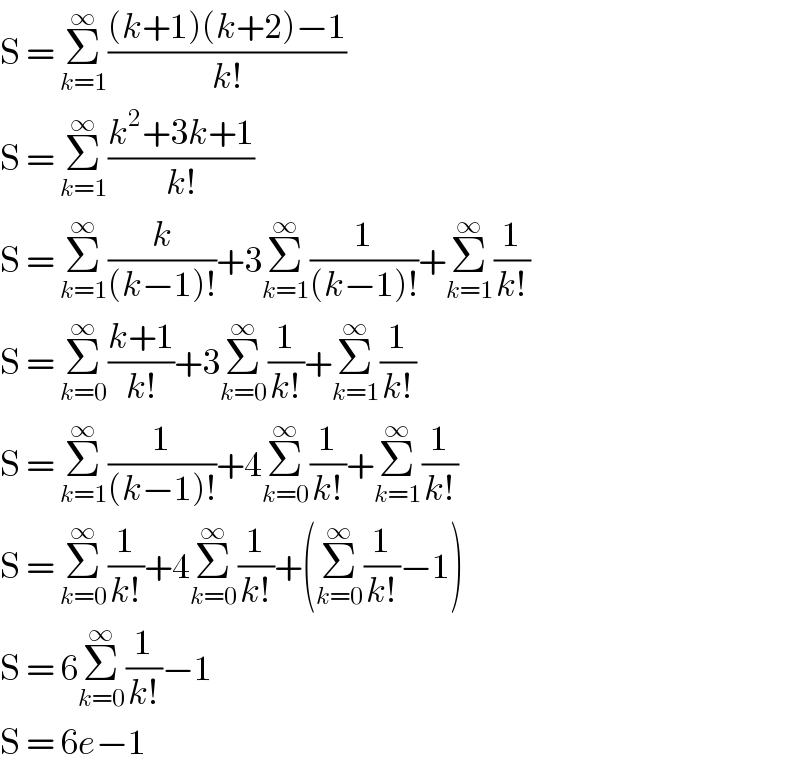
S = Σ_(k=1) ^∞ (((k+1)(k+2)−1)/(k!)) S = Σ_(k=1) ^∞ ((k^2 +3k+1)/(k!)) S = Σ_(k=1) ^∞ (k/((k−1)!))+3Σ_(k=1) ^∞ (1/((k−1)!))+Σ_(k=1) ^∞ (1/(k!)) S = Σ_(k=0) ^∞ ((k+1)/(k!))+3Σ_(k=0) ^∞ (1/(k!))+Σ_(k=1) ^∞ (1/(k!)) S = Σ_(k=1) ^∞ (1/((k−1)!))+4Σ_(k=0) ^∞ (1/(k!))+Σ_(k=1) ^∞ (1/(k!)) S = Σ_(k=0) ^∞ (1/(k!))+4Σ_(k=0) ^∞ (1/(k!))+(Σ_(k=0) ^∞ (1/(k!))−1) S = 6Σ_(k=0) ^∞ (1/(k!))−1 S = 6e−1

$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)−\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{2}} +\mathrm{3}{k}+\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}}{\left({k}−\mathrm{1}\right)!}+\mathrm{3}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{k}+\mathrm{1}}{{k}!}+\mathrm{3}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!}+\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\mathrm{4}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}+\left(\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}−\mathrm{1}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{6}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}−\mathrm{1} \\ $$$$\mathrm{S}\:=\:\mathrm{6}{e}−\mathrm{1} \\ $$

Commented by Dwaipayan Shikari last updated on 22/Jul/20

��

Commented by Dwaipayan Shikari last updated on 22/Jul/20

Great solution

$${Great}\:{solution} \\ $$

Commented by mr W last updated on 22/Jul/20

i agree with MJS sir. in fact the sum of LHS is not unique, since the a_n term is not defined!

$${i}\:{agree}\:{with}\:{MJS}\:{sir}.\:{in}\:{fact}\:{the} \\ $$$${sum}\:{of}\:{LHS}\:{is}\:{not}\:{unique},\:{since}\:{the} \\ $$$${a}_{{n}} \:{term}\:{is}\:{not}\:{defined}! \\ $$

Commented by 1549442205PVT last updated on 22/Jul/20

we can find out the rule to define general term follows as: a_1 =5,a_2 =11,a_3 =19,a_4 =29,a_5 =41.So, determinant (((a_2 −a_1 ),(a_3 −a_2 ),(a_4 −a_3 ),(a_5 −a_4 )),(6,8,(10),(12))) Since 12−10=10−8=8−6 ,it follows that the sequence 6,8,10,12 ...form an arithmetic progression which has the difference equal to 2.Hence its general term is 2n+4.So,by above result a_(n+1) −a_n =2n+4.It follows that Σ_(k=1) ^n (a_(k+1) −a_k )=Σ_(k=1) ^(n) (2k+4) ⇒a_(n+1) −a_1 =2Σ_(k=1) ^(n) k+4n=n(n+1)+4n ⇒a_(n+1) =n^2 +5n+5⇒a_n =n^2 +3n+1

$$\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{out}\:\mathrm{the}\:\mathrm{rule}\:\mathrm{to}\:\mathrm{define}\: \\ $$$$\mathrm{general}\:\mathrm{term}\:\mathrm{follows}\:\mathrm{as}: \\ $$$$\mathrm{a}_{\mathrm{1}} =\mathrm{5},\mathrm{a}_{\mathrm{2}} =\mathrm{11},\mathrm{a}_{\mathrm{3}} =\mathrm{19},\mathrm{a}_{\mathrm{4}} =\mathrm{29},\mathrm{a}_{\mathrm{5}} =\mathrm{41}.\mathrm{So}, \\ $$$$\begin{vmatrix}{\mathrm{a}_{\mathrm{2}} −\mathrm{a}_{\mathrm{1}} }&{\mathrm{a}_{\mathrm{3}} −\mathrm{a}_{\mathrm{2}} }&{\mathrm{a}_{\mathrm{4}} −\mathrm{a}_{\mathrm{3}} }&{\mathrm{a}_{\mathrm{5}} −\mathrm{a}_{\mathrm{4}} }\\{\mathrm{6}}&{\mathrm{8}}&{\mathrm{10}}&{\mathrm{12}}\end{vmatrix} \\ $$$$\mathrm{Since}\:\mathrm{12}−\mathrm{10}=\mathrm{10}−\mathrm{8}=\mathrm{8}−\mathrm{6}\:,\mathrm{it}\:\mathrm{follows} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{6},\mathrm{8},\mathrm{10},\mathrm{12}\:...\mathrm{form} \\ $$$$\mathrm{an}\:\mathrm{arithmetic}\:\mathrm{progression}\:\mathrm{which}\:\mathrm{has} \\ $$$$\mathrm{the}\:\mathrm{difference}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{2}.\mathrm{Hence}\:\mathrm{its} \\ $$$$\mathrm{general}\:\mathrm{term}\:\mathrm{is}\:\mathrm{2n}+\mathrm{4}.\mathrm{So},\mathrm{by}\:\mathrm{above}\:\mathrm{result} \\ $$$$\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{n}} =\mathrm{2n}+\mathrm{4}.\mathrm{It}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{a}_{\mathrm{k}+\mathrm{1}} −\mathrm{a}_{\mathrm{k}} \right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\left(\mathrm{2k}+\mathrm{4}\right) \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{n}+\mathrm{1}} −\mathrm{a}_{\mathrm{1}} =\mathrm{2}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\mathrm{k}+\mathrm{4n}=\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{4n} \\ $$$$\Rightarrow\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}+\mathrm{1}} =\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{5}\boldsymbol{\mathrm{n}}+\mathrm{5}\Rightarrow\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} =\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{\mathrm{n}}+\mathrm{1} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com