
Question Number 104542 by mohammad17 last updated on 22/Jul/20

Answered by Dwaipayan Shikari last updated on 22/Jul/20

$$\left.\mathrm{2}\right) \\ $$$${tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)={log}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\frac{\frac{\mathrm{1}}{{x}}.\frac{{dy}}{{dx}}−\frac{{y}}{{x}^{\mathrm{2}} }}{\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }+\mathrm{1}}=\frac{\mathrm{2}{x}+\mathrm{2}{y}\frac{{dy}}{{dx}}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${x}\frac{{dy}}{{dx}}−{y}=\mathrm{2}{x}+\mathrm{2}{y}\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}{x}+{y}}{{x}−\mathrm{2}{y}} \\ $$
Commented by mohammad17 last updated on 22/Jul/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Jul/20
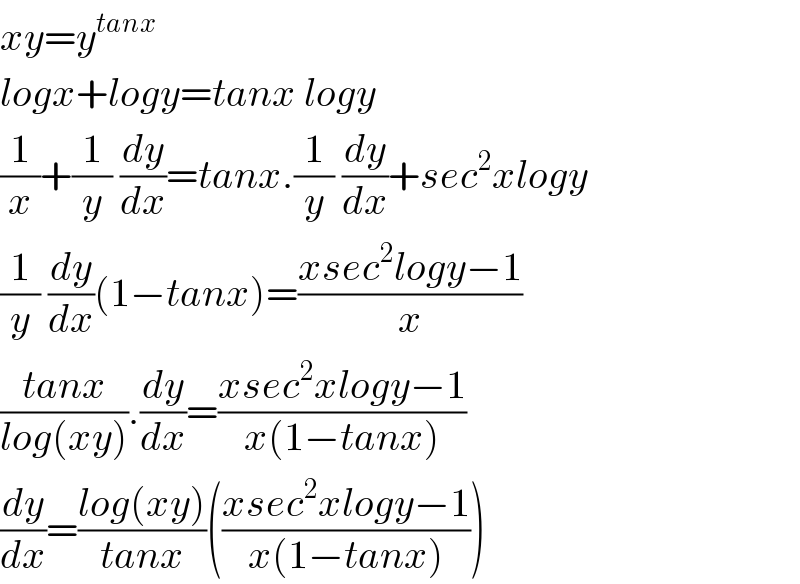
$${xy}={y}^{{tanx}} \\ $$$${logx}+{logy}={tanx}\:{logy} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}}={tanx}.\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}}+{sec}^{\mathrm{2}} {xlogy} \\ $$$$\frac{\mathrm{1}}{{y}}\:\frac{{dy}}{{dx}}\left(\mathrm{1}−{tanx}\right)=\frac{{xsec}^{\mathrm{2}} {logy}−\mathrm{1}}{{x}} \\ $$$$\frac{{tanx}}{{log}\left({xy}\right)}.\frac{{dy}}{{dx}}=\frac{{xsec}^{\mathrm{2}} {xlogy}−\mathrm{1}}{{x}\left(\mathrm{1}−{tanx}\right)} \\ $$$$\frac{{dy}}{{dx}}=\frac{{log}\left({xy}\right)}{{tanx}}\left(\frac{{xsec}^{\mathrm{2}} {xlogy}−\mathrm{1}}{{x}\left(\mathrm{1}−{tanx}\right)}\right) \\ $$
Commented by mohammad17 last updated on 22/Jul/20

Commented by mohammad17 last updated on 22/Jul/20
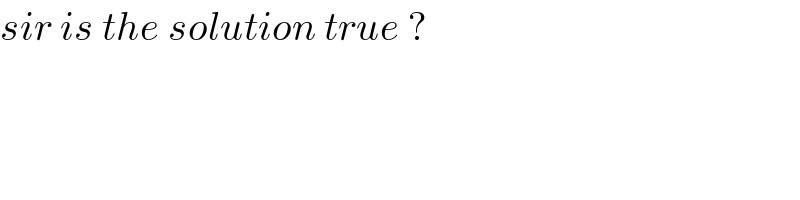
$${sir}\:{is}\:{the}\:{solution}\:{true}\:? \\ $$
Commented by Dwaipayan Shikari last updated on 22/Jul/20

$${yes} \\ $$
