
Question Number 10455 by amir last updated on 10/Feb/17

Commented by mrW1 last updated on 10/Feb/17

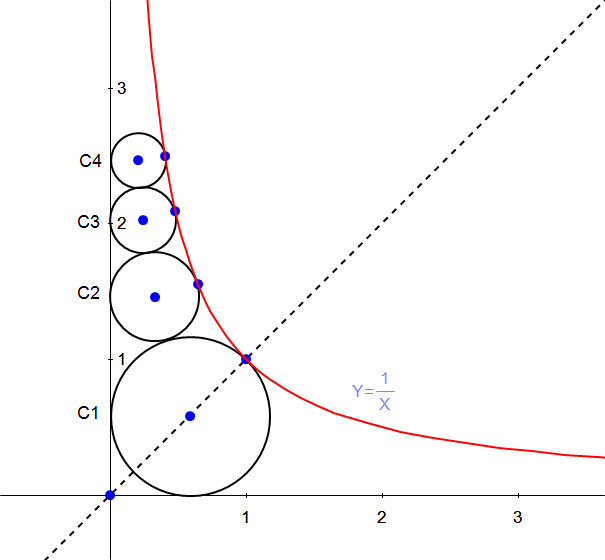
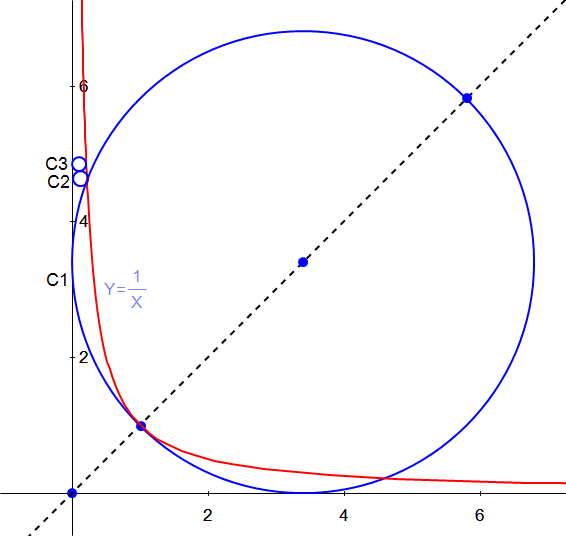
$${circle}\:{C}\mathrm{1}\:{with}\:{radius}\:{r}_{\mathrm{1}} \:{and}\:{centre} \\ $$$${point}\:{M}_{\mathrm{1}} \left({r}_{\mathrm{1}} ,{h}_{\mathrm{1}} \right){with}\:{h}_{\mathrm{1}} ={r}_{\mathrm{1}} \:{has}\:{two} \\ $$$${possibilities}: \\ $$$${r}_{\mathrm{1}} =\begin{cases}{\mathrm{2}−\sqrt{\mathrm{2}}}\\{\mathrm{2}+\sqrt{\mathrm{2}}}\end{cases} \\ $$$$ \\ $$$${circle}\:{C}\mathrm{2}\:{with}\:{radius}\:{r}_{\mathrm{2}} \:{and}\:{centre} \\ $$$${point}\:{M}_{\mathrm{2}} \left({r}_{\mathrm{2}} ,{h}_{\mathrm{2}} \right) \\ $$$$\left({h}_{\mathrm{2}} −{h}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)^{\mathrm{2}} =\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow{h}_{\mathrm{2}} ={h}_{\mathrm{1}} +\mathrm{2}\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }={r}_{\mathrm{1}} +\mathrm{2}\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{2}} } \\ $$$$ \\ $$$${equation}\:{of}\:{circle}\:{C}\mathrm{2}\:{is} \\ $$$$\left({x}−{r}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}−{h}_{\mathrm{2}} \right)^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\left({x}−{r}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}−{r}_{\mathrm{1}} −\mathrm{2}\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }\right)^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${it}\:{tangents}\:{the}\:{curve}\:{xy}=\mathrm{1} \\ $$$$\left({x}−{r}_{\mathrm{2}} \right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{x}}−{r}_{\mathrm{1}} −\mathrm{2}\sqrt{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }\right)^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:\:\:...\left({i}\right) \\ $$$$ \\ $$$${way}\:\mathrm{1}: \\ $$$${solve}\:{x}\:{in}\:{terms}\:{of}\:{r}_{\mathrm{2}} \:\left({I}\:{know}\:{this}\:{is}\:{not}\:{easy}\right) \\ $$$${since}\:{there}\:{is}\:{only}\:{one}\:{solution}\:{for}\:{x}\:\left({tangent}!\right) \\ $$$$\Rightarrow{solution}\:{for}\:{r}_{\mathrm{2}} \\ $$$$\Rightarrow{determine}\:{h}_{\mathrm{2}} \\ $$$$ \\ $$$${way}\:\mathrm{2}: \\ $$$${solve}\:{r}_{\mathrm{2}} \:{in}\:{terms}\:{of}\:{x}\:\left({I}\:{know}\:{this}\:{is}\:{not}\:{easy}\right) \\ $$$${since}\:{r}_{\mathrm{2}} \:{must}\:{be}\:{minimum}\:\left({tangent}!\right) \\ $$$$\Rightarrow\frac{{dr}_{\mathrm{2}} }{{dx}}=\mathrm{0} \\ $$$$\Rightarrow{solve}\:{x} \\ $$$$\Rightarrow{determine}\:{r}_{\mathrm{2}} \\ $$$$\Rightarrow{determine}\:{h}_{\mathrm{2}} \\ $$$$ \\ $$$${with}\:{r}_{\mathrm{2}} \:{and}\:{h}_{\mathrm{2}} \:{you}\:{can}\:{determine}\: \\ $$$${r}_{\mathrm{3}} \:{and}\:{h}_{\mathrm{3}} \:{for}\:{circle}\:{C}\mathrm{3}\:{in}\:{similary}\:{way}... \\ $$$${etc}... \\ $$$$ \\ $$$${I}\:{don}'{t}\:{think}\:{there}\:{exists}\:{a}\:{general} \\ $$$${formula}\:{for}\:{circle}\:{C}_{{n}} \:\left({n}=\mathrm{2},\mathrm{3},...\mathrm{20},...\right) \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Feb/17

$${hello}\:{dear}\:{mrW}\mathrm{1}.{please}\:{draw}\:{a}\: \\ $$$${diagram}\:{in}\:{large}\:{scale}\:{and}\:{post}\:{it}\: \\ $$$${here}.{i}\:{will}\:{solve}\:{this}\:{quiestion}.\: \\ $$$${tnx}\mathrm{4}{all}. \\ $$
Commented by mrW1 last updated on 14/Feb/17
Commented by mrW1 last updated on 14/Feb/17
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Mar/17
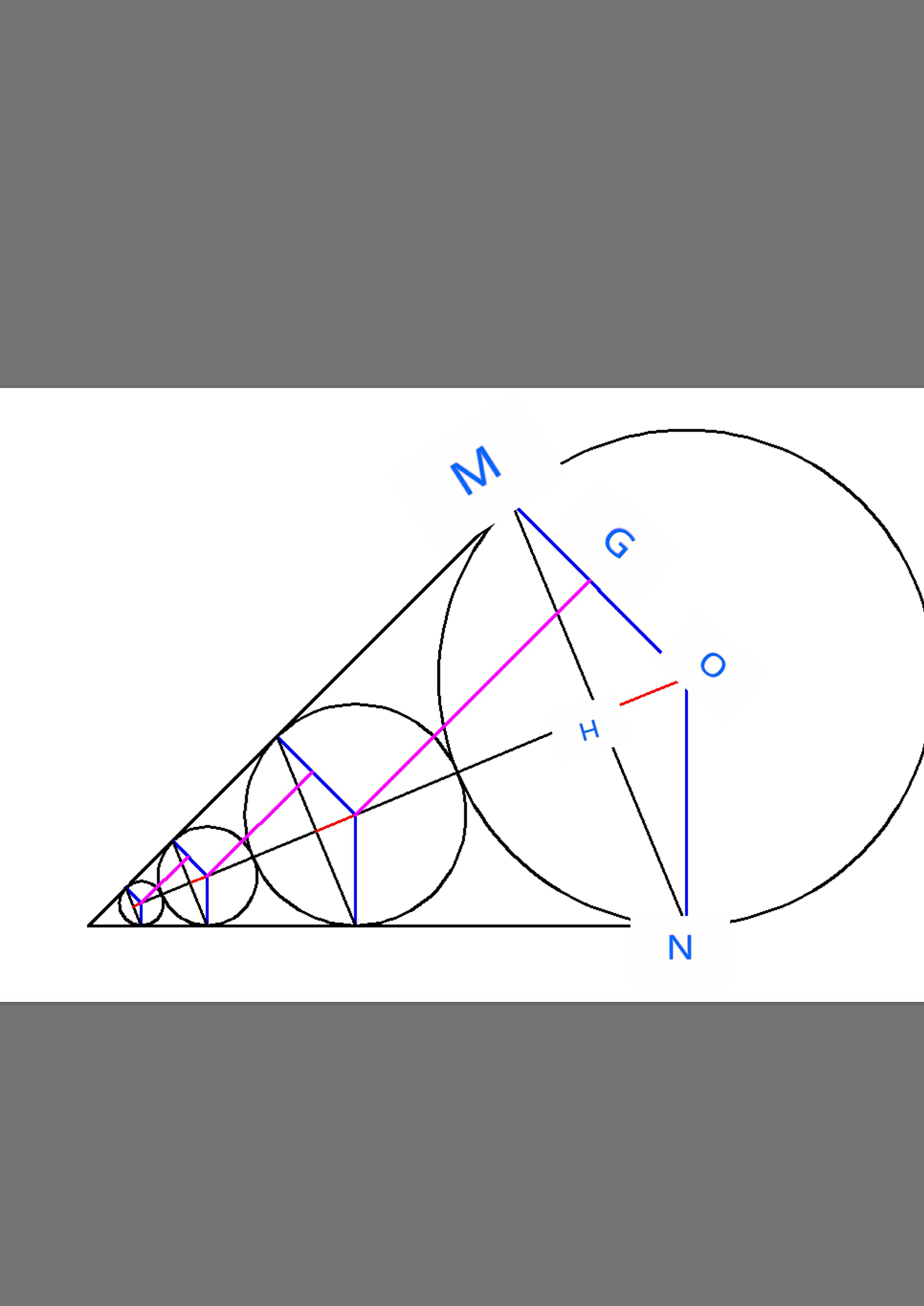
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Mar/17
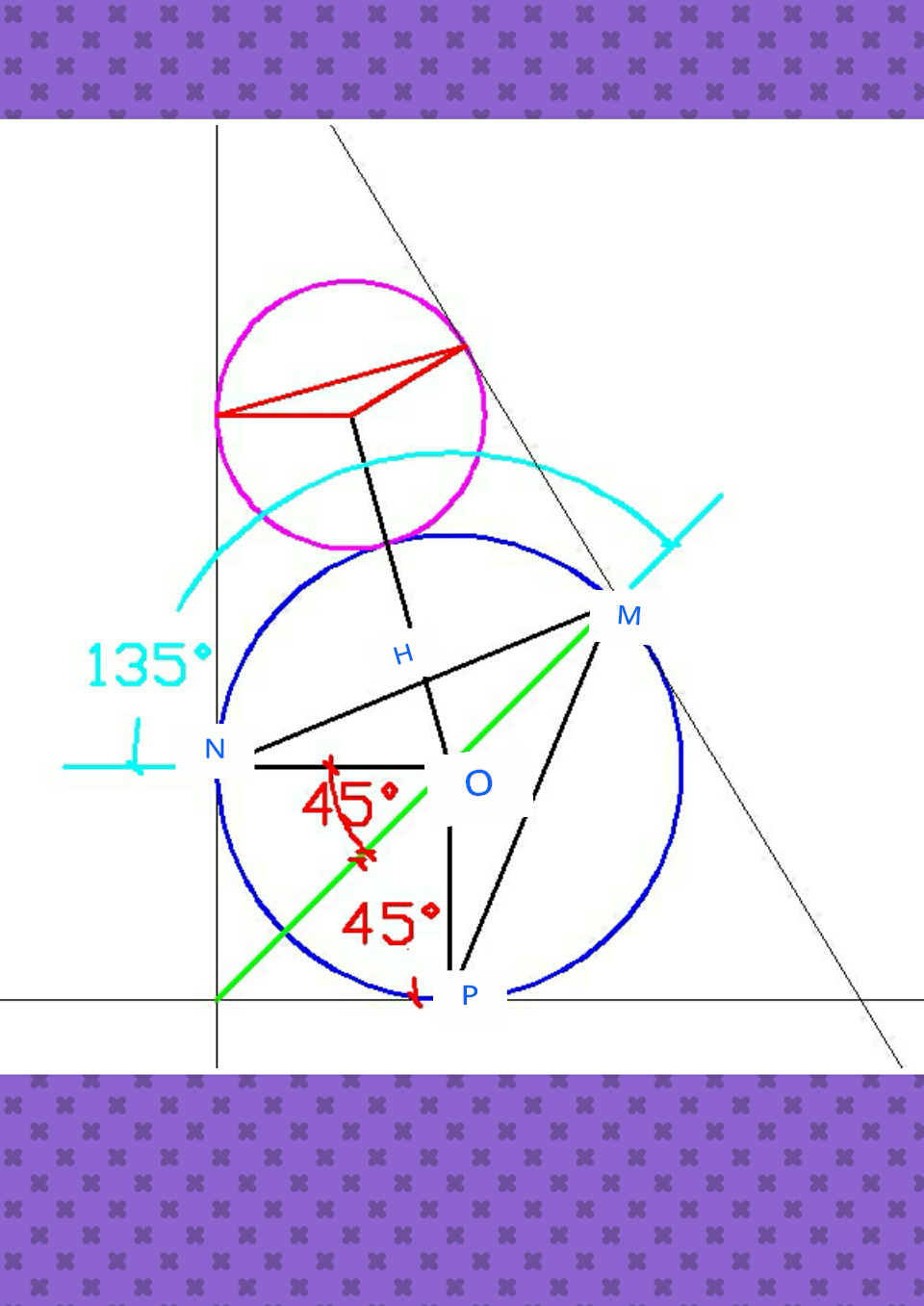
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Mar/17
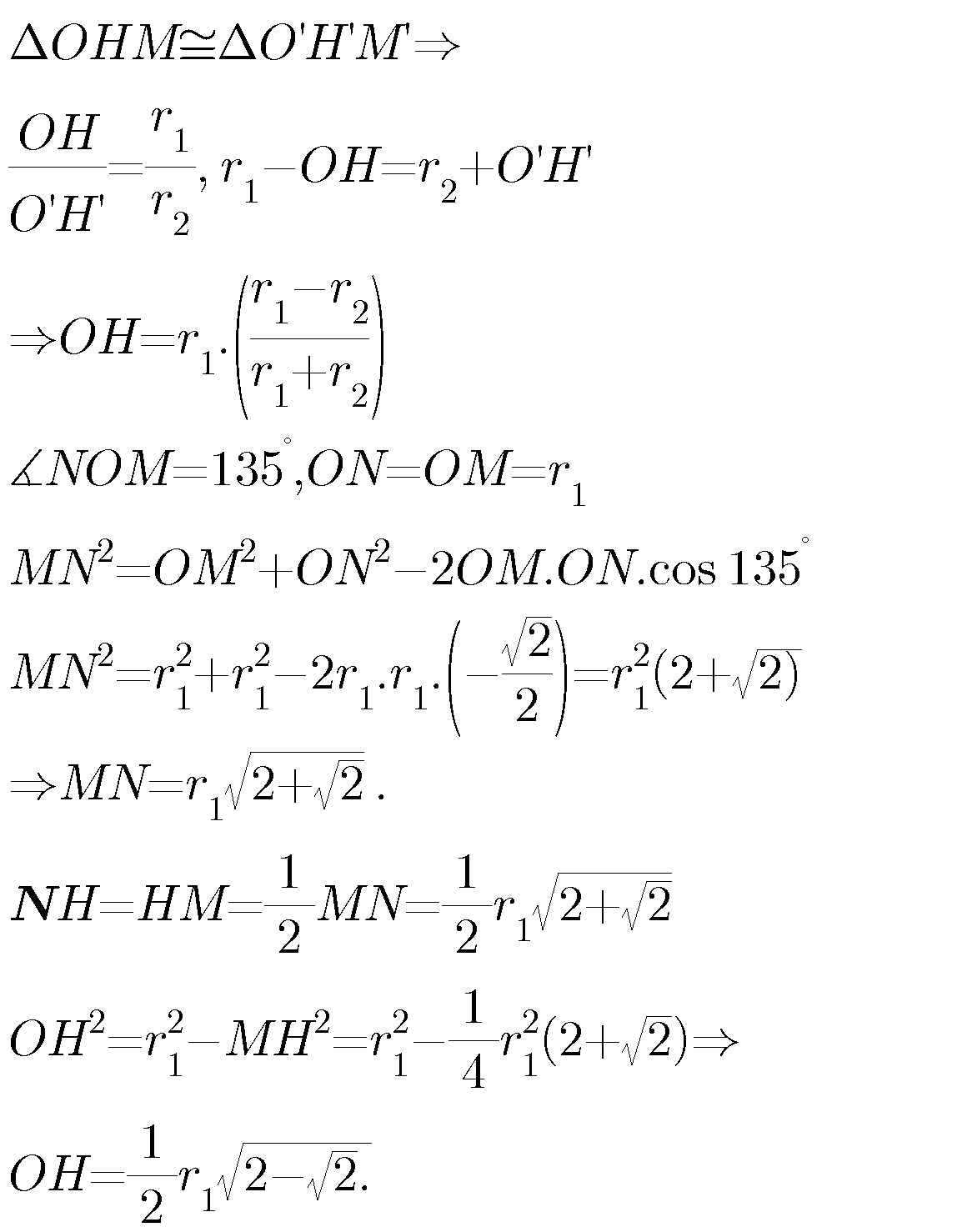
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Mar/17
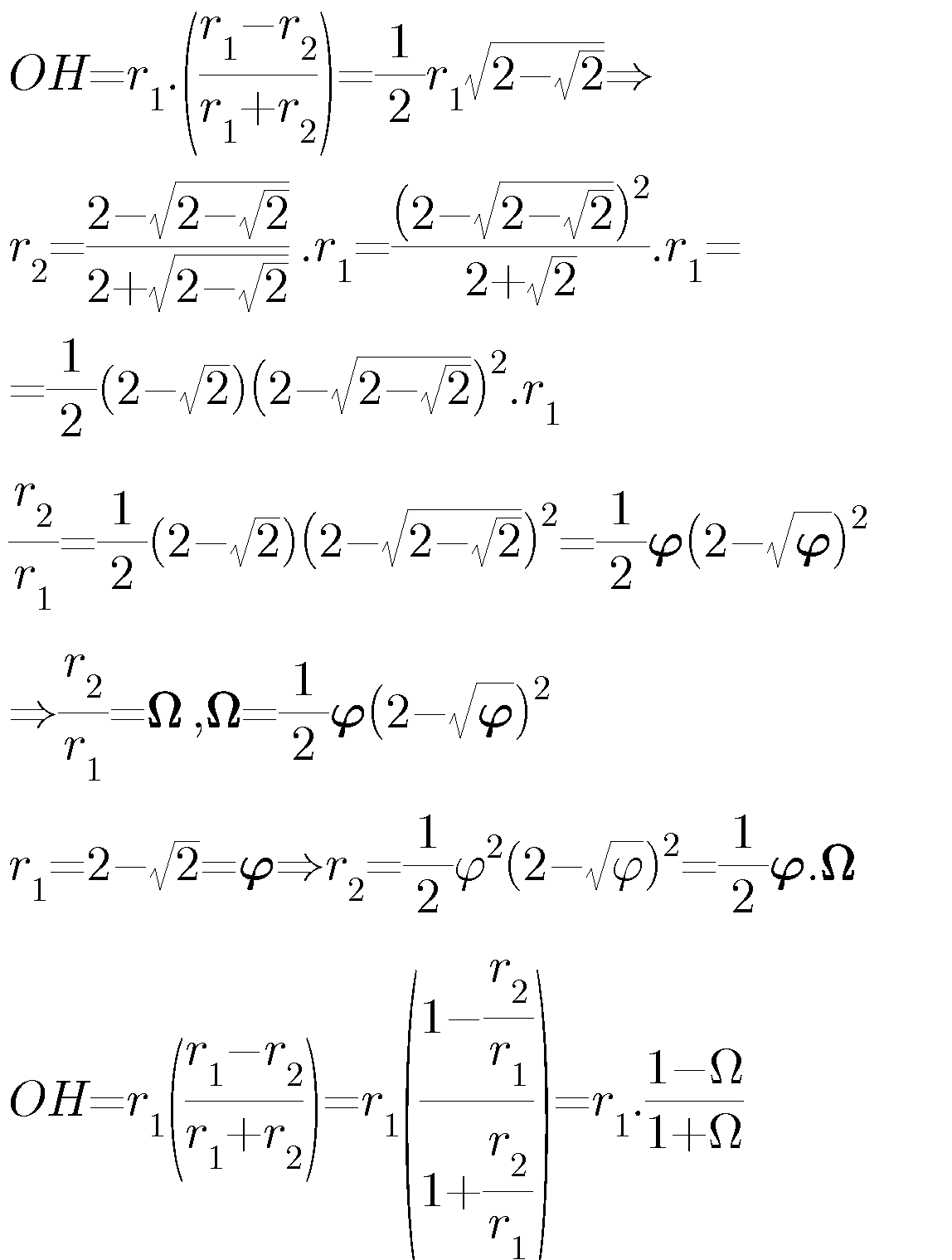
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Mar/17
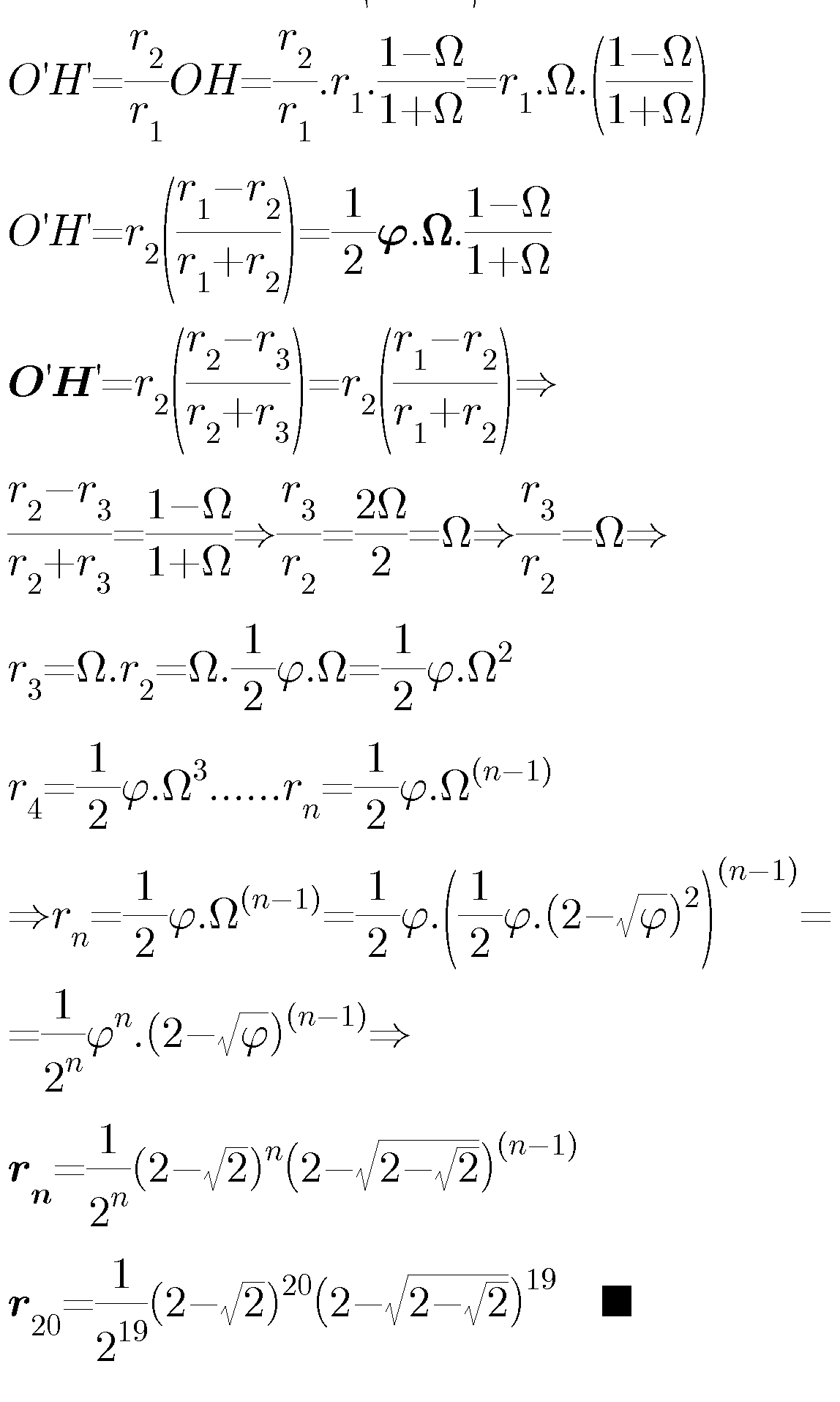
Commented by mrW1 last updated on 16/Mar/17
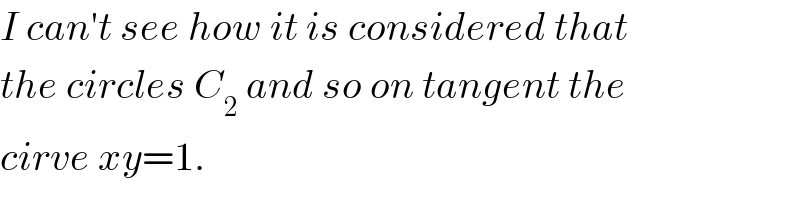
$${I}\:{can}'{t}\:{see}\:{how}\:{it}\:{is}\:{considered}\:{that} \\ $$$${the}\:{circles}\:{C}_{\mathrm{2}} \:{and}\:{so}\:{on}\:{tangent}\:{the} \\ $$$${cirve}\:{xy}=\mathrm{1}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Mar/17
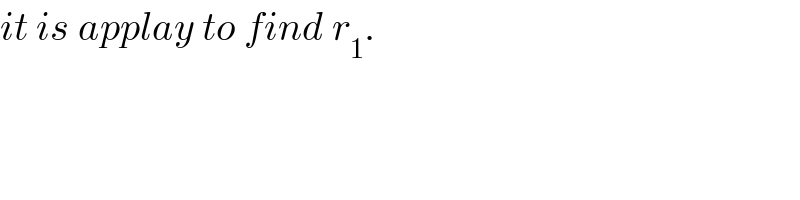
$${it}\:{is}\:{applay}\:{to}\:{find}\:{r}_{\mathrm{1}} . \\ $$
