
Question Number 104572 by ajfour last updated on 22/Jul/20
Commented by ajfour last updated on 22/Jul/20

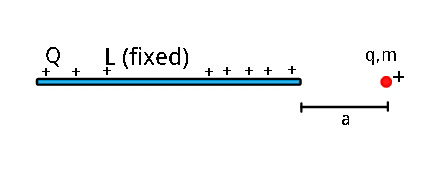
$${A}\:{point}\:{charge}\:{q}\:{with}\:{mass}\:{m} \\ $$$${is}\:{released}\:{at}\:{a}\:{distance}\:\boldsymbol{{a}}\:{from} \\ $$$${a}\:{fixed}\:{uniformly}\:{charged}\:{rod} \\ $$$${of}\:{length}\:{L},\:{charge}\:{Q}.\:{Find}\:{the} \\ $$$${speed}\:{acquired}\:{by}\:{point}\:{charge} \\ $$$${q}\:{as}\:{it}\:{reaches}\:{an}\:{infinite} \\ $$$${distance}\:{from}\:{the}\:{rod}. \\ $$
Answered by OlafThorendsen last updated on 22/Jul/20
![E = (Q/(2πε_0 )).(1/x).(1/(x+L)) F = qE = mx^(••) ((qQ)/(2πε_0 )).(1/(x(x+L))) = mx^(••) ((qQ)/(2πε_0 L)).(x^• /(x(x+L))) = mx^(••) x^• (with v = x^• ) ((qQ)/(2πε_0 L^2 ))x^• [(1/x)−(1/(x+L))] = mx^(••) x^• ((qQ)/(2πε_0 L^2 )).ln(x/(x+L)) = (1/2)mv^2 +C t = 0, v = 0 ⇒ C = −((qQ)/(2πε_0 L^2 )).ln(a/(a+L)) (1/2)mv^2 = ((qQ)/(2πε_0 L^2 ))(ln(x/(x+L))−ln(a/(a+L))) v_∞ ^2 = ((qQ)/(πε_0 mL^2 ))ln((a+L)/a) ...may be](Q104598.png)
$$\mathrm{E}\:=\:\frac{\mathrm{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} }.\frac{\mathrm{1}}{{x}}.\frac{\mathrm{1}}{{x}+\mathrm{L}} \\ $$$$\mathrm{F}\:=\:{q}\mathrm{E}\:=\:{m}\overset{\bullet\bullet} {{x}} \\ $$$$\frac{{q}\mathrm{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} }.\frac{\mathrm{1}}{{x}\left({x}+\mathrm{L}\right)}\:=\:{m}\overset{\bullet\bullet} {{x}} \\ $$$$\frac{{q}\mathrm{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} \mathrm{L}}.\frac{\overset{\bullet} {{x}}}{{x}\left({x}+\mathrm{L}\right)}\:=\:{m}\overset{\bullet\bullet} {{x}}\overset{\bullet} {{x}}\:\left(\mathrm{with}\:{v}\:=\:\overset{\bullet} {{x}}\right) \\ $$$$\frac{{q}\mathrm{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} \mathrm{L}^{\mathrm{2}} }\overset{\bullet} {{x}}\left[\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{L}}\right]\:=\:{m}\overset{\bullet\bullet} {{x}}\overset{\bullet} {{x}} \\ $$$$\frac{{q}\mathrm{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} \mathrm{L}^{\mathrm{2}} }.\mathrm{ln}\frac{{x}}{{x}+\mathrm{L}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +\mathrm{C} \\ $$$${t}\:=\:\mathrm{0},\:{v}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{C}\:=\:−\frac{{q}\mathrm{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} \mathrm{L}^{\mathrm{2}} }.\mathrm{ln}\frac{{a}}{{a}+\mathrm{L}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \:=\:\frac{{q}\mathrm{Q}}{\mathrm{2}\pi\epsilon_{\mathrm{0}} \mathrm{L}^{\mathrm{2}} }\left(\mathrm{ln}\frac{{x}}{{x}+\mathrm{L}}−\mathrm{ln}\frac{{a}}{{a}+\mathrm{L}}\right) \\ $$$${v}_{\infty} ^{\mathrm{2}} \:=\:\frac{{q}\mathrm{Q}}{\pi\epsilon_{\mathrm{0}} {m}\mathrm{L}^{\mathrm{2}} }\mathrm{ln}\frac{{a}+\mathrm{L}}{{a}} \\ $$$$...{may}\:{be} \\ $$
Commented by ajfour last updated on 22/Jul/20
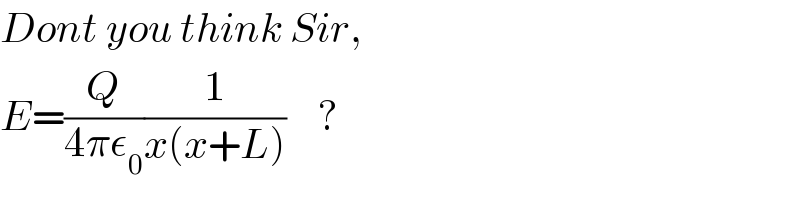
$${Dont}\:{you}\:{think}\:{Sir}, \\ $$$${E}=\frac{{Q}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\frac{\mathrm{1}}{{x}\left({x}+{L}\right)}\:\:\:\:? \\ $$
