
Question Number 10458 by paonky last updated on 10/Feb/17
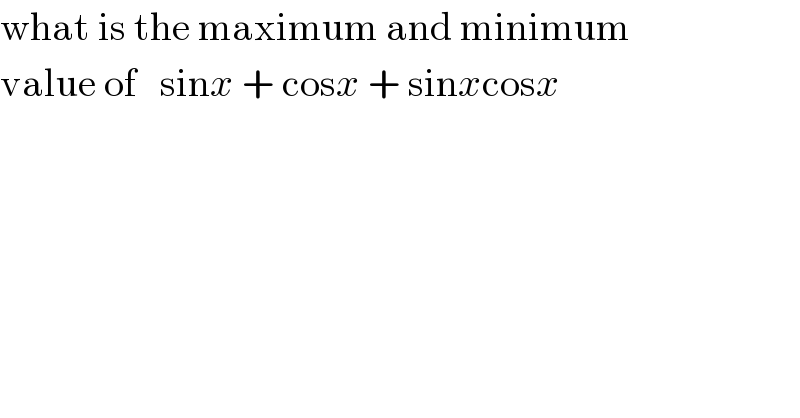
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{and}\:\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\:\:\mathrm{sin}{x}\:+\:\mathrm{cos}{x}\:+\:\mathrm{sin}{x}\mathrm{cos}{x} \\ $$
Answered by mrW1 last updated on 10/Feb/17
![sinx +cos x =(√2)(sin x×((√2)/2)+cos x×((√2)/2)) =(√2)(sin x×cos (π/4)+cos x×sin (π/4)) =(√2)sin (x+(π/4)) sin xcos x=(1/2)sin 2x=−(1/2)cos (2x+(π/2)) =−(1/2)cos 2(x+(π/4))=−(1/2)[1−2sin^2 (x+(π/4))] =sin^2 (x+(π/4))−(1/2) f=sinx + cosx + sinxcosx =(√2)sin (x+(π/4))+sin^2 (x+(π/4))−(1/2) =(((√2)/2))^2 +2×((√2)/2)sin (x+(π/4))+sin^2 (x+(π/4))−1 =[((√2)/2)+sin (x+(π/4))]^2 −1 when sin (x+(π/4))=−((√2)/2) , i.e. x=π+2iπ or x=((3π)/2)+2iπ ⇒ f_(min) =−1 when sin (x+(π/4))=1, i.e. x=(π/4)+2iπ ⇒ f_(max) =(((√2)/2)+1)^2 −1=(1/2)+(√2)≈1.914](Q10459.png)
$$\mathrm{sin}{x}\:+\mathrm{cos}\:{x} \\ $$$$=\sqrt{\mathrm{2}}\left(\mathrm{sin}\:{x}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\mathrm{cos}\:{x}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$=\sqrt{\mathrm{2}}\left(\mathrm{sin}\:{x}×\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+\mathrm{cos}\:{x}×\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\sqrt{\mathrm{2}}\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{sin}\:{x}\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}\left({x}+\frac{\pi}{\mathrm{4}}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\left({x}+\frac{\pi}{\mathrm{4}}\right)\right] \\ $$$$=\mathrm{sin}^{\mathrm{2}} \:\left({x}+\frac{\pi}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${f}=\mathrm{sin}{x}\:+\:\mathrm{cos}{x}\:+\:\mathrm{sin}{x}\mathrm{cos}{x} \\ $$$$=\sqrt{\mathrm{2}}\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{sin}^{\mathrm{2}} \:\left({x}+\frac{\pi}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{sin}^{\mathrm{2}} \:\left({x}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{1} \\ $$$$=\left[\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\right]^{\mathrm{2}} −\mathrm{1} \\ $$$$ \\ $$$${when}\:\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:,\:{i}.{e}.\:{x}=\pi+\mathrm{2}{i}\pi\:{or}\:{x}=\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{2}{i}\pi \\ $$$$\Rightarrow\:{f}_{{min}} =−\mathrm{1} \\ $$$${when}\:\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{1},\:{i}.{e}.\:{x}=\frac{\pi}{\mathrm{4}}+\mathrm{2}{i}\pi \\ $$$$\Rightarrow\:{f}_{{max}} =\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{2}}\approx\mathrm{1}.\mathrm{914} \\ $$
Commented by paonky last updated on 10/Feb/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
