Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 104604 by ~blr237~ last updated on 22/Jul/20

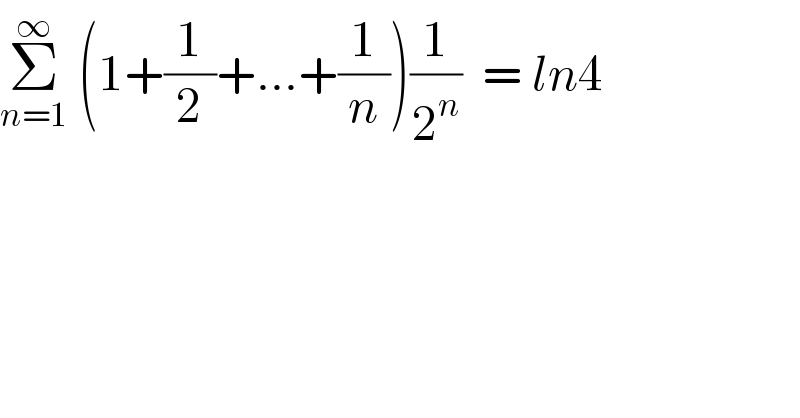
Σ_(n=1) ^∞ (1+(1/2)+...+(1/n))(1/2^n ) = ln4

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+...+\frac{\mathrm{1}}{{n}}\right)\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\:=\:{ln}\mathrm{4} \\ $$

Answered by OlafThorendsen last updated on 22/Jul/20

S = Σ_(n=1) ^∞ (1+(1/2)+...+(1/n))(1/2^n ) S = Σ_(n=1) ^∞ (1/2^n )Σ_(k=1) ^n (1/k) S = Σ_(n=1) ^∞ (1/n)Σ_(k=n) ^∞ (1/2^k ) S = lim_(N→∞) Σ_(n=1) ^∞ (1/n).(1/2^n ).((1−((1/2))^N )/(1−(1/2))) S = 2Σ_(n=1) ^∞ (1/n).(1/2^n ) S = 2Σ_(n=1) ^∞ (2^(−n) /n) (1/(1−x)) = Σ_(n=0) ^∞ x^k , ∣x∣<1 −ln∣1−x∣ = Σ_(n=1) ^∞ (x^k /k) S = 2Σ_(n=1) ^∞ (2^(−n) /n) = −2ln∣1−(1/2)∣ S = 2Σ_(n=1) ^∞ (2^(−n) /n) = −2ln(1/2) = ln4

$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+...+\frac{\mathrm{1}}{{n}}\right)\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\underset{{k}={n}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} } \\ $$$$\mathrm{S}\:=\:\underset{\mathrm{N}\rightarrow\infty} {\mathrm{lim}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}.\frac{\mathrm{1}}{\mathrm{2}^{{n}} }.\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{N}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{S}\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}.\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{S}\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{−{n}} }{{n}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{k}} ,\:\mid{x}\mid<\mathrm{1} \\ $$$$−\mathrm{ln}\mid\mathrm{1}−{x}\mid\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{k}} }{{k}} \\ $$$$\mathrm{S}\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{−{n}} }{{n}}\:=\:−\mathrm{2ln}\mid\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mid \\ $$$$\mathrm{S}\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{−{n}} }{{n}}\:=\:−\mathrm{2ln}\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{ln4} \\ $$

Commented by ~blr237~ last updated on 23/Jul/20

Nice work Sir

$${Nice}\:{work}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com