Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 104608 by ~blr237~ last updated on 22/Jul/20

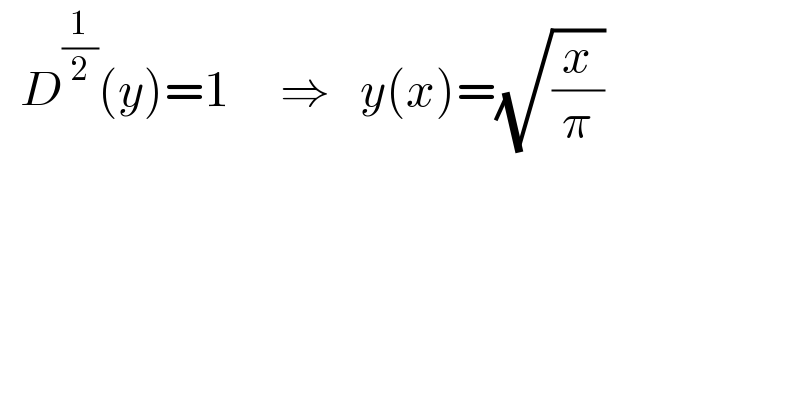
$$D^{\frac{1}{2}}\left(y\right)=1\Rightarrow y\left(x\right)=\sqrt{\frac{x}{\pi }}$$

Answered by OlafThorendsen last updated on 22/Jul/20

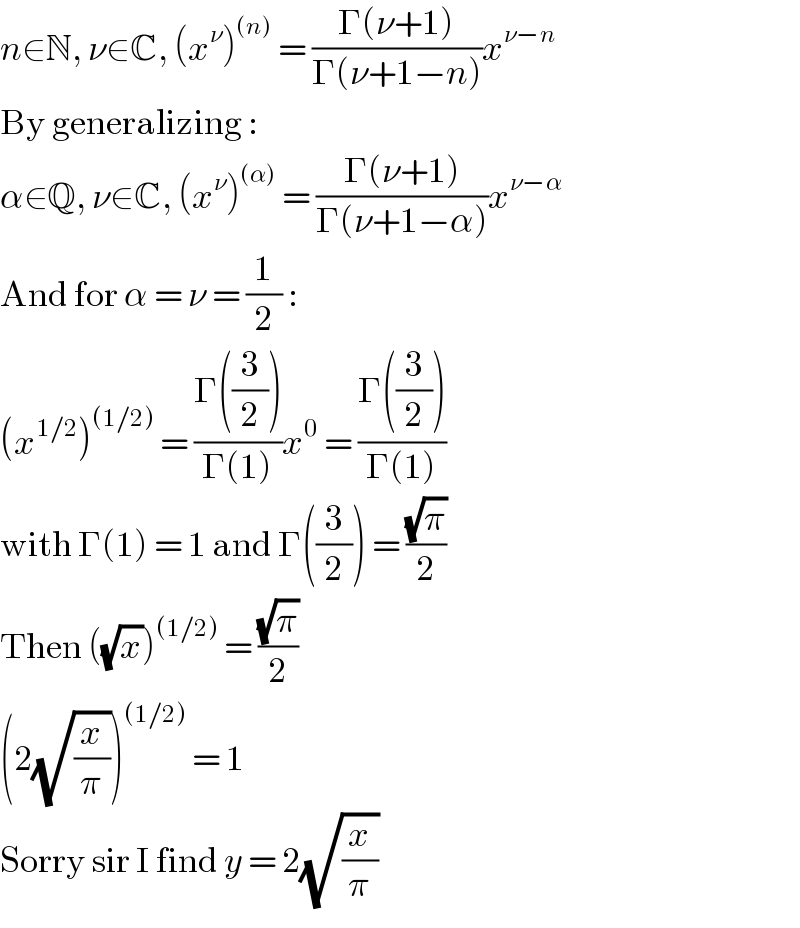
$$n\in \mathbb{N},\nu \in \mathbb{C},{\left(x^{\nu }\right)}^{\left(n\right)}=\frac{\mathrm{\Gamma }(\nu +1)}{\mathrm{\Gamma }(\nu +1-n)}{x}^{\nu -n}$$$$\mathrm{By}\mathrm{generalizing}:$$$$\alpha \in \mathbb{Q},\nu \in \mathbb{C},{\left(x^{\nu }\right)}^{\left(\alpha \right)}=\frac{\mathrm{\Gamma }(\nu +1)}{\mathrm{\Gamma }(\nu +1-\alpha )}{x}^{\nu -\alpha }$$$$\mathrm{And}\mathrm{for}\alpha =\nu =\frac{1}{2}:$$$${\left(x^{1/2}\right)}^{\left(1/2\right)}=\frac{\mathrm{\Gamma }\left(\frac{3}{2}\right)}{\mathrm{\Gamma }\left(1\right)}{x}^0=\frac{\mathrm{\Gamma }\left(\frac{3}{2}\right)}{\mathrm{\Gamma }\left(1\right)}$$$$\mathrm{with}\mathrm{\Gamma }\left(1\right)=1\mathrm{and}\mathrm{\Gamma }\left(\frac{3}{2}\right)=\frac{\sqrt{\pi }}{2}$$$$\mathrm{Then}{\left(\sqrt{x}\right)}^{\left(1/2\right)}=\frac{\sqrt{\pi }}{2}$$$${\left(2\sqrt{\frac{x}{\pi }}\right)}^{\left(1/2\right)}=1$$$$\mathrm{Sorry}\mathrm{sir}\mathrm{I}\mathrm{find}y=2\sqrt{\frac{x}{\pi }}$$

Commented by ~blr237~ last updated on 23/Jul/20

$$yes{it}^{\prime }scorrect:erroroftypo$$$$Butyou{didn}^{\prime }tprovethepropositiononlyitsinterplay$$$$Thatgeneralisationisalsocorrect\left({it}^{\prime }stheCaputoderivation\right)andthatcoincideswiththeRiemann-Liouvillederivationwhen\alpha =\frac{1}{2}$$$$D^{\alpha }\left(f\right)\left(x\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}\frac{d}{dx}\left({\int }_0^x{t}^{\alpha -1}f(x-t)dt\right)0<\alpha$$$$D^{\frac{1}{2}}\left(y\right)=1\Rightarrow D^{\frac{1}{2}}\left(D^{\frac{1}{2}}\left(y\right)\right)=D^{\frac{1}{2}}\left(1\right)$$$$\Rightarrow y^{\prime }\left(x\right)=\frac{1}{\mathrm{\Gamma }\left(\frac{1}{2}\right)}\frac{d}{dx}\left(2\sqrt{x}\right)$$$$\Rightarrow y\left(x\right)=2\sqrt{\frac{x}{\pi }}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com