
Question Number 104644 by Rohit@Thakur last updated on 22/Jul/20
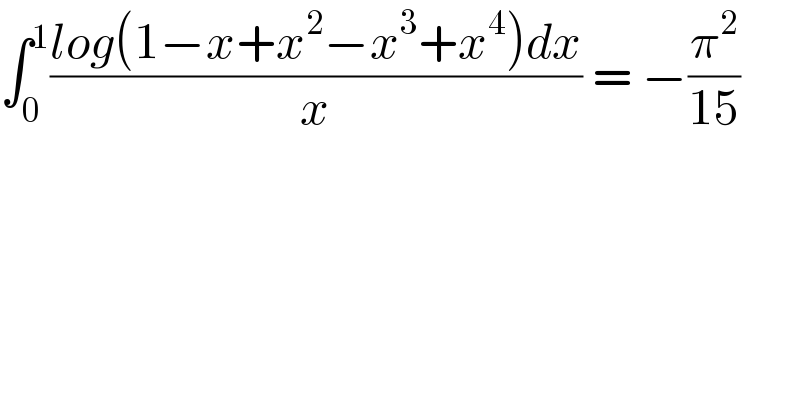
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right){dx}}{{x}}\:=\:−\frac{\pi^{\mathrm{2}} }{\mathrm{15}} \\ $$
Answered by mathmax by abdo last updated on 23/Jul/20

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} \:+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\frac{\mathrm{1}−\left(−\mathrm{x}\right)^{\mathrm{5}} }{\mathrm{1}−\left(−\mathrm{x}\right)}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \:\:\:\mathrm{for}\:\mid\mathrm{u}\mid<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\mathrm{c}\left(\mathrm{c}=\mathrm{0}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{u}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:=−\delta\left(\mathrm{2}\right)\:=−\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{x}^{\mathrm{5n}} \:\Rightarrow\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)}{\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{x}^{\mathrm{5n}−\mathrm{1}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)}{\mathrm{x}}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}\left(\mathrm{5n}\right)}\:=−\frac{\mathrm{1}}{\mathrm{5}}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{5}}×\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{60}} \\ $$$$\Rightarrow\:\mathrm{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{60}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:=\left(\frac{\mathrm{1}}{\mathrm{60}}−\frac{\mathrm{1}}{\mathrm{12}}\right)\pi^{\mathrm{2}} \:=\frac{\mathrm{1}−\mathrm{5}}{\mathrm{60}}×\pi^{\mathrm{2}} \:=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{60}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{15}} \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{proved}. \\ $$$$ \\ $$
