Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 104651 by Ar Brandon last updated on 23/Jul/20

Consider the differential equation; x′′(t)+x(t)=t^2 cos(2t). Knowing that the Complementary Function is; y_(CF) =acos(t)+bsin(t), In what form can the particular integral be expressed so as to obtain the general solution to the given differential equation?

$$\mathrm{Consider}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation}; \\ $$$$\mathrm{x}''\left(\mathrm{t}\right)+\mathrm{x}\left(\mathrm{t}\right)=\mathrm{t}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{2t}\right). \\ $$$$\mathrm{Knowing}\:\mathrm{that}\:\mathrm{the}\:\mathrm{Complementary}\:\mathrm{Function}\:\mathrm{is}; \\ $$$$\mathrm{y}_{\mathrm{CF}} =\mathrm{acos}\left(\mathrm{t}\right)+\mathrm{bsin}\left(\mathrm{t}\right), \\ $$$$\mathrm{In}\:\mathrm{what}\:\mathrm{form}\:\mathrm{can}\:\mathrm{the}\:\mathrm{particular}\:\mathrm{integral}\:\mathrm{be}\:\mathrm{expressed} \\ $$$$\mathrm{so}\:\mathrm{as}\:\mathrm{to}\:\mathrm{obtain}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{the}\:\mathrm{given}\: \\ $$$$\mathrm{differential}\:\mathrm{equation}? \\ $$

Answered by mathmax by abdo last updated on 23/Jul/20

y_h =acost +bsint =au_1 (t)+bu_2 (t) W(u_1 ,u_2 ) = determinant (((cost sint)),((−sint cost)))=cos^2 t +sin^2 t =1 ≠0 W_1 = determinant (((0 sint)),((t^2 cos2t cost)))=−t^2 sint cos(2t) W_2 = determinant (((cost 0)),((−sint t^2 cos(2t))))=t^2 cost cos(2t) v_1 =∫ (w_1 /w)dx =−∫ t^2 sint cos(2t)dt we have sint cos(2t) =cos((π/2)−t)cos(2t) =(1/2) { cos((π/2)−t +2t) +cos((π/2)−t−2t)}=(1/2){−sint +sin(3t)} ⇒ v_1 =−(1/2)∫(−sint +sin(3t)t^2 dt =(1/2) ∫ t^2 sint dt−(1/2) ∫t^2 sin(3t)dt (1/2)∫t^2 sint dt=(1/2){ −t^(2 ) cost +∫ 2t cost dt} =−(t^2 /2)cost +2 { tsint −∫ sint dt} =−(t^2 /2)cost +2{ tsint +cost} ∫t^2 sin(3t)dt =_(3t =u) ∫(u^2 /9)sin(u)(du/3) =(1/(27)) ∫ u^2 sinu du =... v_2 =∫ ((w2)/w)dx =∫ t^2 cost cos(2t)dt =(1/2)∫ t^2 {cos(3t) +cos(t)}dt=... the particular solution is x_p =u_1 v_1 +u_2 v_2 and the general solution is x (t) =x_h (t)+x_p (t)

$$\mathrm{y}_{\mathrm{h}} =\mathrm{acost}\:+\mathrm{bsint}\:\:=\mathrm{au}_{\mathrm{1}} \left(\mathrm{t}\right)+\mathrm{bu}_{\mathrm{2}} \left(\mathrm{t}\right) \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{cost}\:\:\:\:\:\:\:\:\:\mathrm{sint}}\\{−\mathrm{sint}\:\:\:\:\:\:\mathrm{cost}}\end{vmatrix}=\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:=\mathrm{1}\:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{sint}}\\{\mathrm{t}^{\mathrm{2}} \mathrm{cos2t}\:\:\mathrm{cost}}\end{vmatrix}=−\mathrm{t}^{\mathrm{2}} \:\mathrm{sint}\:\mathrm{cos}\left(\mathrm{2t}\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{cost}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\mathrm{sint}\:\:\:\:\:\:\mathrm{t}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{2t}\right)}\end{vmatrix}=\mathrm{t}^{\mathrm{2}} \:\mathrm{cost}\:\mathrm{cos}\left(\mathrm{2t}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\mathrm{t}^{\mathrm{2}} \:\mathrm{sint}\:\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{sint}\:\mathrm{cos}\left(\mathrm{2t}\right)\:=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{t}\right)\mathrm{cos}\left(\mathrm{2t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\:\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{t}\:+\mathrm{2t}\right)\:+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{t}−\mathrm{2t}\right)\right\}=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{sint}\:+\mathrm{sin}\left(\mathrm{3t}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\left(−\mathrm{sint}\:+\mathrm{sin}\left(\mathrm{3t}\right)\mathrm{t}^{\mathrm{2}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\mathrm{t}^{\mathrm{2}} \:\mathrm{sint}\:\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{2}}\:\int\mathrm{t}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{3t}\right)\mathrm{dt}\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{t}^{\mathrm{2}} \mathrm{sint}\:\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:−\mathrm{t}^{\mathrm{2}\:} \mathrm{cost}\:+\int\:\mathrm{2t}\:\mathrm{cost}\:\mathrm{dt}\right\}\:=−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\mathrm{cost}\:+\mathrm{2}\:\left\{\:\:\mathrm{tsint}\:−\int\:\mathrm{sint}\:\mathrm{dt}\right\} \\ $$$$=−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\mathrm{cost}\:+\mathrm{2}\left\{\:\mathrm{tsint}\:+\mathrm{cost}\right\} \\ $$$$\int\mathrm{t}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3t}\right)\mathrm{dt}\:=_{\mathrm{3t}\:=\mathrm{u}} \:\:\int\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{9}}\mathrm{sin}\left(\mathrm{u}\right)\frac{\mathrm{du}}{\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{27}}\:\int\:\mathrm{u}^{\mathrm{2}} \:\mathrm{sinu}\:\mathrm{du}\:=... \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w2}}{\mathrm{w}}\mathrm{dx}\:=\int\:\mathrm{t}^{\mathrm{2}} \:\mathrm{cost}\:\mathrm{cos}\left(\mathrm{2t}\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{t}^{\mathrm{2}} \left\{\mathrm{cos}\left(\mathrm{3t}\right)\:+\mathrm{cos}\left(\mathrm{t}\right)\right\}\mathrm{dt}=... \\ $$$$\mathrm{the}\:\mathrm{particular}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{x}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \:\mathrm{v}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{x}\:\left(\mathrm{t}\right)\:=\mathrm{x}_{\mathrm{h}} \left(\mathrm{t}\right)+\mathrm{x}_{\mathrm{p}} \left(\mathrm{t}\right) \\ $$

Commented by Ar Brandon last updated on 23/Jul/20

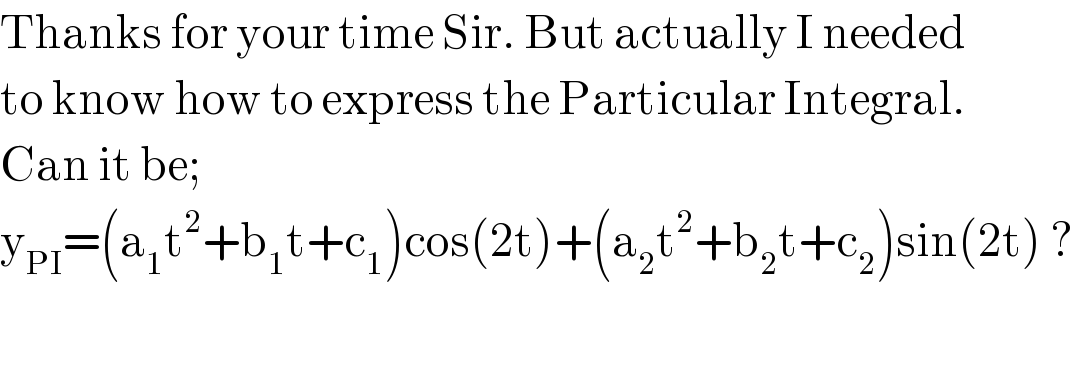
Thanks for your time Sir. But actually I needed to know how to express the Particular Integral. Can it be; y_(PI) =(a_1 t^2 +b_1 t+c_1 )cos(2t)+(a_2 t^2 +b_2 t+c_2 )sin(2t) ?

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{Sir}.\:\mathrm{But}\:\mathrm{actually}\:\mathrm{I}\:\mathrm{needed} \\ $$$$\mathrm{to}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{express}\:\mathrm{the}\:\mathrm{Particular}\:\mathrm{Integral}. \\ $$$$\mathrm{Can}\:\mathrm{it}\:\mathrm{be}; \\ $$$$\mathrm{y}_{\mathrm{PI}} =\left(\mathrm{a}_{\mathrm{1}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}_{\mathrm{1}} \mathrm{t}+\mathrm{c}_{\mathrm{1}} \right)\mathrm{cos}\left(\mathrm{2t}\right)+\left(\mathrm{a}_{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{b}_{\mathrm{2}} \mathrm{t}+\mathrm{c}_{\mathrm{2}} \right)\mathrm{sin}\left(\mathrm{2t}\right)\:? \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com