Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 104655 by bobhans last updated on 23/Jul/20

lim_(x→a) (((√(2x+a))−(√(3x)))/((√(x+3a))−2(√x))) =? [a≠0]

$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{\sqrt{\mathrm{2}{x}+{a}}−\sqrt{\mathrm{3}{x}}}{\sqrt{{x}+\mathrm{3}{a}}−\mathrm{2}\sqrt{{x}}}\:=?\:\:\:\:\left[{a}\neq\mathrm{0}\right]\: \\ $$

Answered by bramlex last updated on 23/Jul/20

lim_(x→a) (([(1/(√(2x+a)))−(3/(2(√(3x))))])/([(1/(2(√(x+3a))))−(1/(√x))])) = (((1/(√(3a)))−(3/(2(√(3a)))))/((1/(4(√a)))−(1/(2(√a))))) = {(2/(2(√(3a))))−(3/(2(√(3a)))) }× (−4(√a) ) = −(1/(2(√(3a)))) × (−4(√a) ) = (2/(√3)) ★ [ for a > 0 ]

$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\:\frac{\left[\frac{\mathrm{1}}{\sqrt{\mathrm{2}{x}+{a}}}−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{3}{x}}}\right]}{\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{3}{a}}}−\frac{\mathrm{1}}{\sqrt{{x}}}\right]}\:=\:\frac{\frac{\mathrm{1}}{\sqrt{\mathrm{3}{a}}}−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{3}{a}}}}{\frac{\mathrm{1}}{\mathrm{4}\sqrt{{a}}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}} \\ $$$$=\:\left\{\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}{a}}}−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{3}{a}}}\:\right\}×\:\left(−\mathrm{4}\sqrt{{a}}\:\right) \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}{a}}}\:×\:\left(−\mathrm{4}\sqrt{{a}}\:\right) \\ $$$$=\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\bigstar\:\:\:\left[\:{for}\:{a}\:>\:\mathrm{0}\:\right]\: \\ $$

Commented by malwaan last updated on 23/Jul/20

(2/(3(√3)))

$$\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\: \\ $$

Answered by john santu last updated on 23/Jul/20

set x = a+p lim_(p→0) (((√(2p+3a)) −(√(3p+3a)))/((√(p+4a))−(√(4p+4a)))) = lim_(p→0) (((√(3a)) {(√(1+((2p)/(3a))))−(√(1+(p/a) )) })/((√(4a)) {(√(1+(p/(4a))))−(√(1+(p/a)))})) = ((√3)/2) × lim_(p→0) (((1+(p/(3a)))−(1+(p/(2a))))/((1+(p/(8a)))−(1+(p/(2a))))) = ((√3)/2)× lim_(p→0) (((−(p/(6a))))/((−((3p)/(8a))))) = ((√3)/2) × ((1/(6a)))×(((8a)/3))= ((8(√3))/(2×3×6)) = ((2(√3))/9)

$${set}\:{x}\:=\:{a}+{p} \\ $$$$\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}{p}+\mathrm{3}{a}}\:−\sqrt{\mathrm{3}{p}+\mathrm{3}{a}}}{\sqrt{{p}+\mathrm{4}{a}}−\sqrt{\mathrm{4}{p}+\mathrm{4}{a}}}\:= \\ $$$$\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{3}{a}}\:\left\{\sqrt{\mathrm{1}+\frac{\mathrm{2}{p}}{\mathrm{3}{a}}}−\sqrt{\mathrm{1}+\frac{{p}}{{a}}\:}\:\right\}}{\sqrt{\mathrm{4}{a}}\:\left\{\sqrt{\mathrm{1}+\frac{{p}}{\mathrm{4}{a}}}−\sqrt{\mathrm{1}+\frac{{p}}{{a}}}\right\}} \\ $$$$=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:×\:\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{{p}}{\mathrm{3}{a}}\right)−\left(\mathrm{1}+\frac{{p}}{\mathrm{2}{a}}\right)}{\left(\mathrm{1}+\frac{{p}}{\mathrm{8}{a}}\right)−\left(\mathrm{1}+\frac{{p}}{\mathrm{2}{a}}\right)} \\ $$$$=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\:\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(−\frac{{p}}{\mathrm{6}{a}}\right)}{\left(−\frac{\mathrm{3}{p}}{\mathrm{8}{a}}\right)} \\ $$$$=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:×\:\left(\frac{\mathrm{1}}{\mathrm{6}{a}}\right)×\left(\frac{\mathrm{8}{a}}{\mathrm{3}}\right)=\:\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{2}×\mathrm{3}×\mathrm{6}} \\ $$$$=\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$

Answered by bemath last updated on 23/Jul/20

standart method lim_(x→a) (((√(x+3a))+2(√x))/((√(2x+a))+(√(3x)))) × lim_(x→a) ((2x+a−3x)/(x+3a−4x)) = ((4(√a))/(2(√(3a)))) × lim_(x→a) ((a−x)/(3(a−x))) = (2/(√3)) × (1/3) = (2/(3(√3))) = ((2(√3))/9) ■

$${standart}\:{method} \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{\sqrt{{x}+\mathrm{3}{a}}+\mathrm{2}\sqrt{{x}}}{\sqrt{\mathrm{2}{x}+{a}}+\sqrt{\mathrm{3}{x}}}\:×\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}+{a}−\mathrm{3}{x}}{{x}+\mathrm{3}{a}−\mathrm{4}{x}}\:= \\ $$$$\frac{\mathrm{4}\sqrt{{a}}}{\mathrm{2}\sqrt{\mathrm{3}{a}}}\:×\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{a}−{x}}{\mathrm{3}\left({a}−{x}\right)}\:= \\ $$$$\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:×\:\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\:\blacksquare \\ $$

Answered by Dwaipayan Shikari last updated on 23/Jul/20

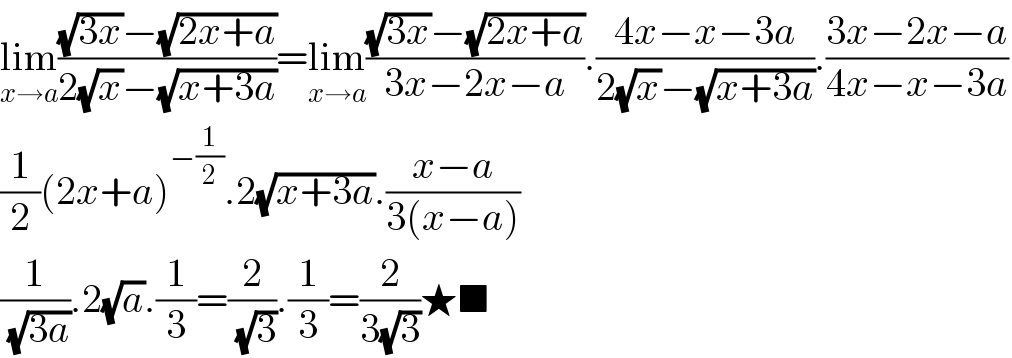
lim_(x→a) (((√(3x))−(√(2x+a)))/(2(√x)−(√(x+3a))))=lim_(x→a) (((√(3x))−(√(2x+a)))/(3x−2x−a)).((4x−x−3a)/(2(√x)−(√(x+3a)))).((3x−2x−a)/(4x−x−3a)) (1/2)(2x+a)^(−(1/2)) .2(√(x+3a)).((x−a)/(3(x−a))) (1/(√(3a))).2(√a).(1/3)=(2/(√3)).(1/3)=(2/(3(√3)))★■

$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{\sqrt{\mathrm{3}{x}}−\sqrt{\mathrm{2}{x}+{a}}}{\mathrm{2}\sqrt{{x}}−\sqrt{{x}+\mathrm{3}{a}}}=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{\sqrt{\mathrm{3}{x}}−\sqrt{\mathrm{2}{x}+{a}}}{\mathrm{3}{x}−\mathrm{2}{x}−{a}}.\frac{\mathrm{4}{x}−{x}−\mathrm{3}{a}}{\mathrm{2}\sqrt{{x}}−\sqrt{{x}+\mathrm{3}{a}}}.\frac{\mathrm{3}{x}−\mathrm{2}{x}−{a}}{\mathrm{4}{x}−{x}−\mathrm{3}{a}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}+{a}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} .\mathrm{2}\sqrt{{x}+\mathrm{3}{a}}.\frac{{x}−{a}}{\mathrm{3}\left({x}−{a}\right)} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{3}{a}}}.\mathrm{2}\sqrt{{a}}.\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}.\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\bigstar\blacksquare \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com