
Question Number 104657 by bobhans last updated on 23/Jul/20
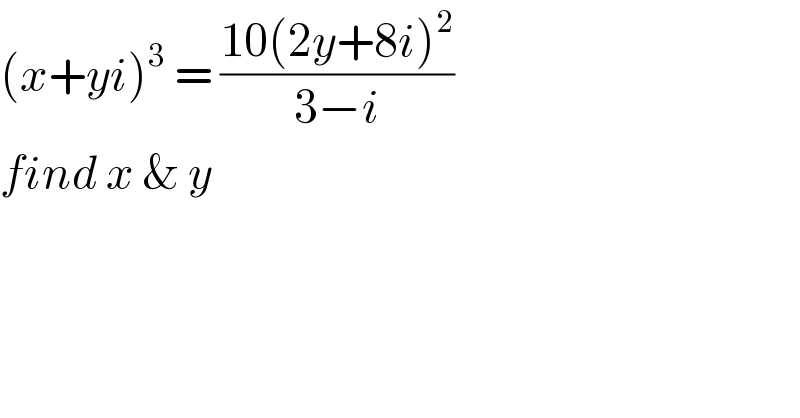
$$\left({x}+{yi}\right)^{\mathrm{3}} \:=\:\frac{\mathrm{10}\left(\mathrm{2}{y}+\mathrm{8}{i}\right)^{\mathrm{2}} }{\mathrm{3}−{i}} \\ $$ $${find}\:{x}\:\&\:{y} \\ $$
Answered by bramlex last updated on 23/Jul/20
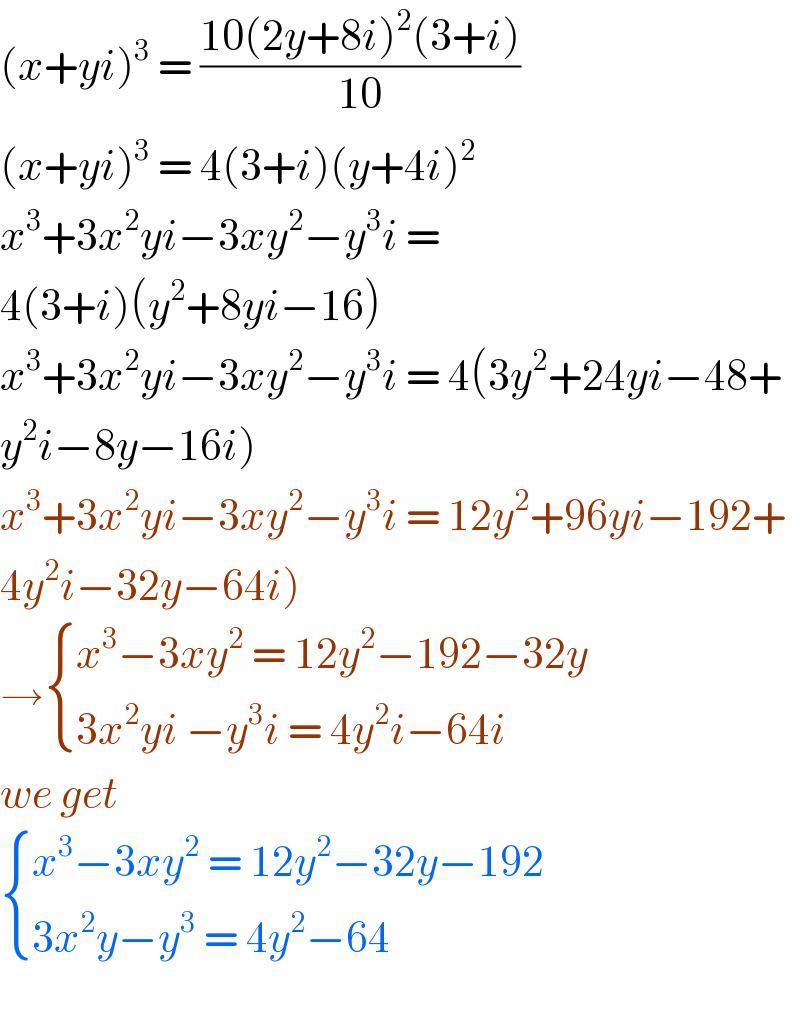
$$\left({x}+{yi}\right)^{\mathrm{3}} \:=\:\frac{\mathrm{10}\left(\mathrm{2}{y}+\mathrm{8}{i}\right)^{\mathrm{2}} \left(\mathrm{3}+{i}\right)}{\mathrm{10}} \\ $$ $$\left({x}+{yi}\right)^{\mathrm{3}} \:=\:\mathrm{4}\left(\mathrm{3}+{i}\right)\left({y}+\mathrm{4}{i}\right)^{\mathrm{2}} \\ $$ $${x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} {yi}−\mathrm{3}{xy}^{\mathrm{2}} −{y}^{\mathrm{3}} {i}\:= \\ $$ $$\mathrm{4}\left(\mathrm{3}+{i}\right)\left({y}^{\mathrm{2}} +\mathrm{8}{yi}−\mathrm{16}\right) \\ $$ $${x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} {yi}−\mathrm{3}{xy}^{\mathrm{2}} −{y}^{\mathrm{3}} {i}\:=\:\mathrm{4}\left(\mathrm{3}{y}^{\mathrm{2}} +\mathrm{24}{yi}−\mathrm{48}+\right. \\ $$ $$\left.{y}^{\mathrm{2}} {i}−\mathrm{8}{y}−\mathrm{16}{i}\right) \\ $$ $${x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} {yi}−\mathrm{3}{xy}^{\mathrm{2}} −{y}^{\mathrm{3}} {i}\:=\:\mathrm{12}{y}^{\mathrm{2}} +\mathrm{96}{yi}−\mathrm{192}+ \\ $$ $$\left.\mathrm{4}{y}^{\mathrm{2}} {i}−\mathrm{32}{y}−\mathrm{64}{i}\right) \\ $$ $$\rightarrow\begin{cases}{{x}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} \:=\:\mathrm{12}{y}^{\mathrm{2}} −\mathrm{192}−\mathrm{32}{y}}\\{\mathrm{3}{x}^{\mathrm{2}} {yi}\:−{y}^{\mathrm{3}} {i}\:=\:\mathrm{4}{y}^{\mathrm{2}} {i}−\mathrm{64}{i}\:\:}\end{cases} \\ $$ $${we}\:{get}\: \\ $$ $$\begin{cases}{{x}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} \:=\:\mathrm{12}{y}^{\mathrm{2}} −\mathrm{32}{y}−\mathrm{192}}\\{\mathrm{3}{x}^{\mathrm{2}} {y}−{y}^{\mathrm{3}} \:=\:\mathrm{4}{y}^{\mathrm{2}} −\mathrm{64}}\end{cases} \\ $$ $$ \\ $$
