Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 104669 by bramlex last updated on 23/Jul/20

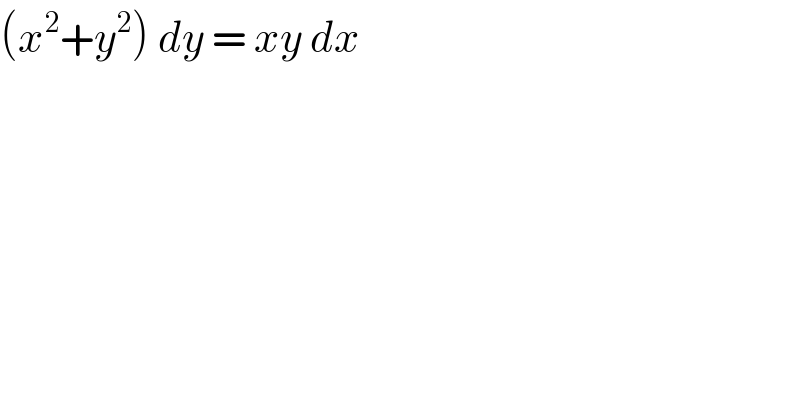
(x^2 +y^2 ) dy = xy dx

$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:{dy}\:=\:{xy}\:{dx}\: \\ $$

Answered by bemath last updated on 23/Jul/20

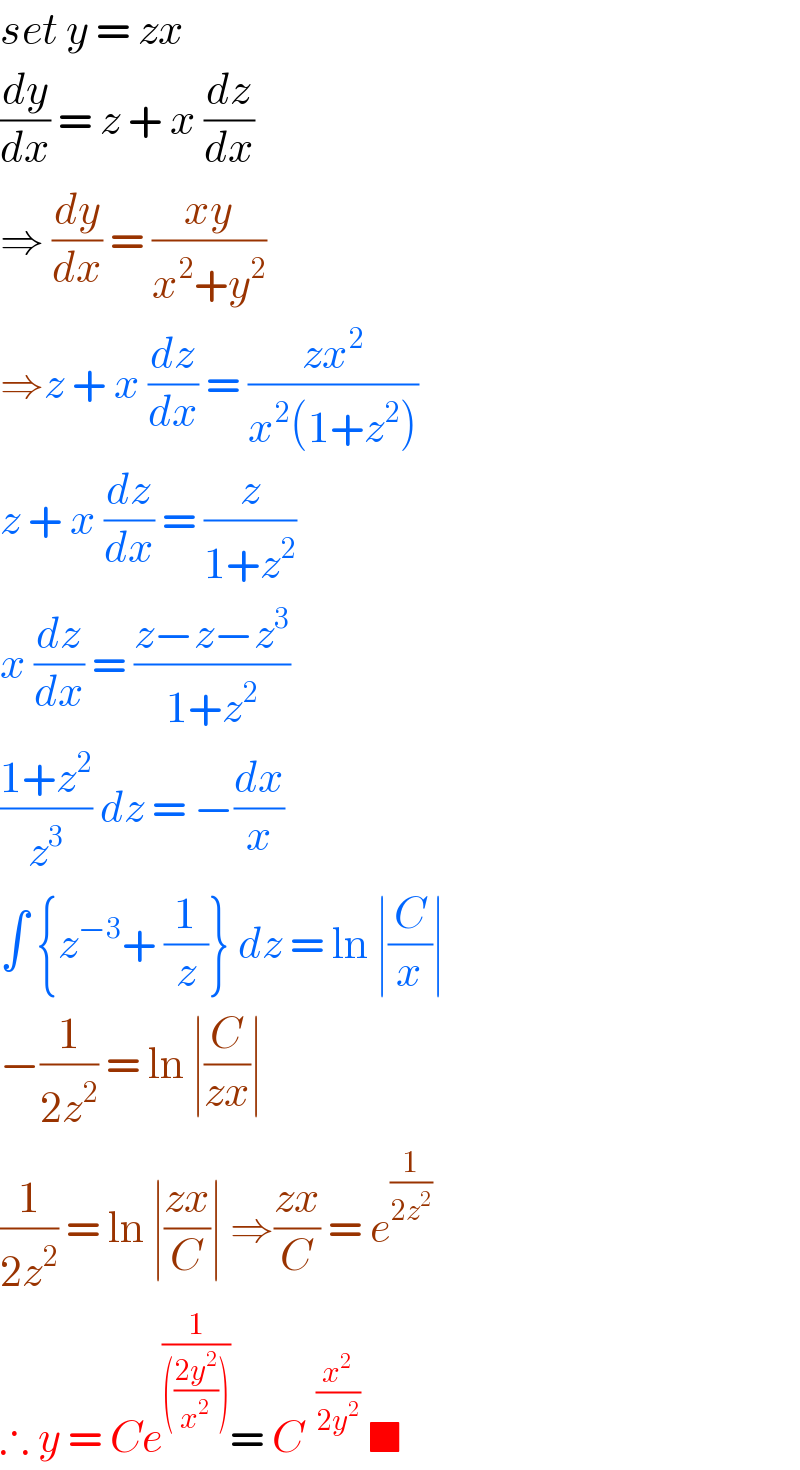
set y = zx (dy/dx) = z + x (dz/dx) ⇒ (dy/dx) = ((xy)/(x^2 +y^2 )) ⇒z + x (dz/dx) = ((zx^2 )/(x^2 (1+z^2 ))) z + x (dz/dx) = (z/(1+z^2 )) x (dz/dx) = ((z−z−z^3 )/(1+z^2 )) ((1+z^2 )/z^3 ) dz = −(dx/x) ∫ {z^(−3) + (1/z)} dz = ln ∣(C/x)∣ −(1/(2z^2 )) = ln ∣(C/(zx))∣ (1/(2z^2 )) = ln ∣((zx)/C)∣ ⇒((zx)/C) = e^(1/(2z^2 )) ∴ y = Ce^(1/((((2y^2 )/x^2 )))) = C^( (x^2 /(2y^2 ))) ■

$${set}\:{y}\:=\:{zx}\: \\ $$$$\frac{{dy}}{{dx}}\:=\:{z}\:+\:{x}\:\frac{{dz}}{{dx}} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\frac{{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\Rightarrow{z}\:+\:{x}\:\frac{{dz}}{{dx}}\:=\:\frac{{zx}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{1}+{z}^{\mathrm{2}} \right)} \\ $$$${z}\:+\:{x}\:\frac{{dz}}{{dx}}\:=\:\frac{{z}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$${x}\:\frac{{dz}}{{dx}}\:=\:\frac{{z}−{z}−{z}^{\mathrm{3}} }{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}+{z}^{\mathrm{2}} }{{z}^{\mathrm{3}} }\:{dz}\:=\:−\frac{{dx}}{{x}} \\ $$$$\int\:\left\{{z}^{−\mathrm{3}} +\:\frac{\mathrm{1}}{{z}}\right\}\:{dz}\:=\:\mathrm{ln}\:\mid\frac{{C}}{{x}}\mid \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} }\:=\:\mathrm{ln}\:\mid\frac{{C}}{{zx}}\mid\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} }\:=\:\mathrm{ln}\:\mid\frac{{zx}}{{C}}\mid\:\Rightarrow\frac{{zx}}{{C}}\:=\:{e}^{\frac{\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} }} \\ $$$$\therefore\:{y}\:=\:{Ce}^{\frac{\mathrm{1}}{\left(\frac{\mathrm{2}{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}} =\:{C}^{\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{y}^{\mathrm{2}} }} \:\blacksquare\: \\ $$

Answered by OlafThorendsen last updated on 23/Jul/20

y(x(dx/dy))−x^2 = y^2 (1/2)yx^2 −∫(1/2)x^2 dy−∫x^2 dy = (y^3 /3)+C_1 u = (1/2)∫x^2 dy yu′−3u = (y^3 /3)+C_1 y^3 u′−3y^2 u = (y^5 /3)+C_1 y^2 ((y^3 u′−3y^2 u)/y^6 ) = (1/(3y))+(C_1 /y^4 ) (d/dy)((u/y^3 )) = (1/(3y))+(C_1 /y^4 ) (u/y^3 ) = (1/3)ln∣y∣+(C_2 /y^3 )+C_3 u = (1/3)y^3 ln∣y∣+C_3 y^3 +C_2 x^2 = 2u′ = 2y^2 ln∣y∣+((2y^2 )/3) +C_4 y^2 x^2 = 2y^2 ln∣y∣ +C_5 y^2 x(y) = ±y(√(lny^2 +C_5 ))

$${y}\left({x}\frac{{dx}}{{dy}}\right)−{x}^{\mathrm{2}} \:=\:{y}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{yx}^{\mathrm{2}} −\int\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} {dy}−\int{x}^{\mathrm{2}} {dy}\:=\:\frac{{y}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{C}_{\mathrm{1}} \\ $$$${u}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int{x}^{\mathrm{2}} {dy} \\ $$$${yu}'−\mathrm{3}{u}\:=\:\frac{{y}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{C}_{\mathrm{1}} \\ $$$${y}^{\mathrm{3}} {u}'−\mathrm{3}{y}^{\mathrm{2}} {u}\:=\:\frac{{y}^{\mathrm{5}} }{\mathrm{3}}+\mathrm{C}_{\mathrm{1}} {y}^{\mathrm{2}} \\ $$$$\frac{{y}^{\mathrm{3}} {u}'−\mathrm{3}{y}^{\mathrm{2}} {u}}{{y}^{\mathrm{6}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}{y}}+\frac{\mathrm{C}_{\mathrm{1}} }{{y}^{\mathrm{4}} } \\ $$$$\frac{{d}}{{dy}}\left(\frac{{u}}{{y}^{\mathrm{3}} }\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}{y}}+\frac{\mathrm{C}_{\mathrm{1}} }{{y}^{\mathrm{4}} } \\ $$$$\frac{{u}}{{y}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid{y}\mid+\frac{\mathrm{C}_{\mathrm{2}} }{{y}^{\mathrm{3}} }+\mathrm{C}_{\mathrm{3}} \\ $$$${u}\:=\:\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} \mathrm{ln}\mid{y}\mid+\mathrm{C}_{\mathrm{3}} {y}^{\mathrm{3}} +\mathrm{C}_{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \:=\:\mathrm{2}{u}'\:=\:\mathrm{2}{y}^{\mathrm{2}} \mathrm{ln}\mid{y}\mid+\frac{\mathrm{2}{y}^{\mathrm{2}} }{\mathrm{3}}\:+\mathrm{C}_{\mathrm{4}} {y}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \:=\:\mathrm{2}{y}^{\mathrm{2}} \mathrm{ln}\mid{y}\mid\:+\mathrm{C}_{\mathrm{5}} {y}^{\mathrm{2}} \\ $$$${x}\left({y}\right)\:=\:\pm{y}\sqrt{\mathrm{ln}{y}^{\mathrm{2}} +\mathrm{C}_{\mathrm{5}} } \\ $$

Answered by Dwaipayan Shikari last updated on 23/Jul/20

(x^2 +v^2 x^2 )dy=vx^2 dx (dy/dx)=(v/(1+v^2 )) (dv/dx)x=((v−v−v^3 )/(1+v^2 )) ∫((1+v^2 )/v^3 )dv=∫−(dx/x) −(1/(2v^2 ))+logv=−logx+C (1/(2v^2 ))=log(vx)+C (x^2 /(2y^2 ))=log(y)+log(C_1 ) y=C_2 e^(x^2 /(2y^2 ))

$$\left({x}^{\mathrm{2}} +{v}^{\mathrm{2}} {x}^{\mathrm{2}} \right){dy}={vx}^{\mathrm{2}} {dx} \\ $$$$\frac{{dy}}{{dx}}=\frac{{v}}{\mathrm{1}+{v}^{\mathrm{2}} } \\ $$$$\frac{{dv}}{{dx}}{x}=\frac{{v}−{v}−{v}^{\mathrm{3}} }{\mathrm{1}+{v}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{1}+{v}^{\mathrm{2}} }{{v}^{\mathrm{3}} }{dv}=\int−\frac{{dx}}{{x}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}{v}^{\mathrm{2}} }+{logv}=−{logx}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{v}^{\mathrm{2}} }={log}\left({vx}\right)+{C} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}{y}^{\mathrm{2}} }={log}\left({y}\right)+{log}\left({C}_{\mathrm{1}} \right) \\ $$$${y}={C}_{\mathrm{2}} {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}{y}^{\mathrm{2}} }} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com