Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104676 by qwertyu last updated on 23/Jul/20

Commented by Dwaipayan Shikari last updated on 23/Jul/20

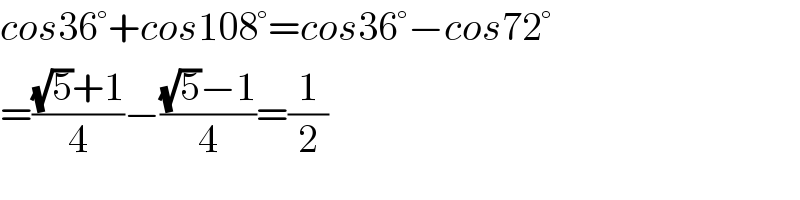
cos36°+cos108°=cos36°−cos72° =(((√5)+1)/4)−(((√5)−1)/4)=(1/2)

$${cos}\mathrm{36}°+{cos}\mathrm{108}°={cos}\mathrm{36}°−{cos}\mathrm{72}° \\ $$$$=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by OlafThorendsen last updated on 23/Jul/20

36° and 72° are not remarkable angles sir. You should prove that cos36° = (((√5)+1)/4) and cos72° = (((√5)−1)/4)

$$\mathrm{36}°\:\mathrm{and}\:\mathrm{72}°\:\mathrm{are}\:\mathrm{not} \\ $$$$\mathrm{remarkable}\:\mathrm{angles}\:\mathrm{sir}. \\ $$$$\mathrm{You}\:\mathrm{should}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{cos36}°\:=\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\:\mathrm{and}\:\mathrm{cos72}°\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$

Commented by Dwaipayan Shikari last updated on 23/Jul/20

θ=18° sin5θ=1 2θ+3θ=(π/2) sin2θ=cos3θ 2sinθcosθ=4cos^3 θ−3cosθ 2sinθ=4cos^2 θ−3 2sinθ=1−4sin^2 θ 4sin^2 θ+2sinθ−1=0 sinθ=((−2+(√(4+16)))/(2.4))=(((√5)−1)/4) sin18°=(((√5)−1)/4)=cos72° cos72°=cos^2 36°−sin^2 36°=2cos^2 36°−1 cos36°=(((√5)+1)/4)

$$\theta=\mathrm{18}° \\ $$$${sin}\mathrm{5}\theta=\mathrm{1} \\ $$$$\mathrm{2}\theta+\mathrm{3}\theta=\frac{\pi}{\mathrm{2}} \\ $$$${sin}\mathrm{2}\theta={cos}\mathrm{3}\theta \\ $$$$\mathrm{2}{sin}\theta{cos}\theta=\mathrm{4}{cos}^{\mathrm{3}} \theta−\mathrm{3}{cos}\theta \\ $$$$\mathrm{2}{sin}\theta=\mathrm{4}{cos}^{\mathrm{2}} \theta−\mathrm{3} \\ $$$$\mathrm{2}{sin}\theta=\mathrm{1}−\mathrm{4}{sin}^{\mathrm{2}} \theta \\ $$$$\mathrm{4}{sin}^{\mathrm{2}} \theta+\mathrm{2}{sin}\theta−\mathrm{1}=\mathrm{0} \\ $$$${sin}\theta=\frac{−\mathrm{2}+\sqrt{\mathrm{4}+\mathrm{16}}}{\mathrm{2}.\mathrm{4}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$${sin}\mathrm{18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}={cos}\mathrm{72}° \\ $$$${cos}\mathrm{72}°={cos}^{\mathrm{2}} \mathrm{36}°−{sin}^{\mathrm{2}} \mathrm{36}°=\mathrm{2}{cos}^{\mathrm{2}} \mathrm{36}°−\mathrm{1} \\ $$$${cos}\mathrm{36}°=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by OlafThorendsen last updated on 23/Jul/20

Waouh. Great method sir!

$$\mathrm{Waouh}.\:\mathrm{Great}\:\mathrm{method}\:\mathrm{sir}! \\ $$$$ \\ $$

Answered by bemath last updated on 23/Jul/20

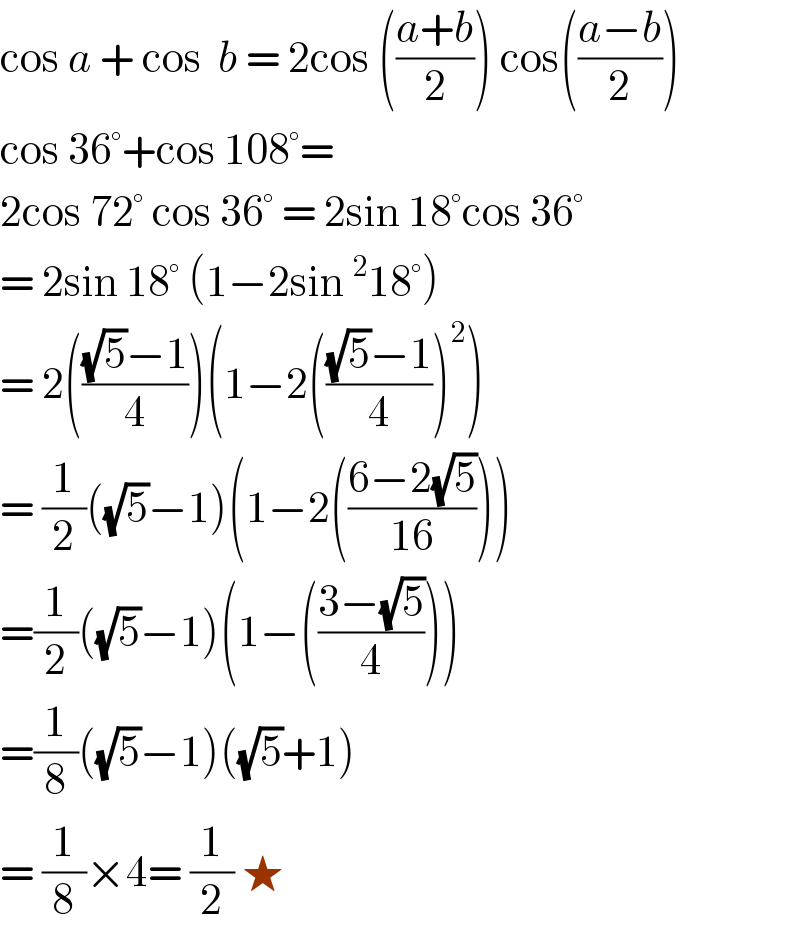
cos a + cos b = 2cos (((a+b)/2)) cos(((a−b)/2)) cos 36°+cos 108°= 2cos 72° cos 36° = 2sin 18°cos 36° = 2sin 18° (1−2sin^2 18°) = 2((((√5)−1)/4))(1−2((((√5)−1)/4))^2 ) = (1/2)((√5)−1)(1−2(((6−2(√5))/(16)))) =(1/2)((√5)−1)(1−(((3−(√5))/4))) =(1/8)((√5)−1)((√5)+1) = (1/8)×4= (1/2) ★

$$\mathrm{cos}\:{a}\:+\:\mathrm{cos}\:\:{b}\:=\:\mathrm{2cos}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\:\mathrm{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right) \\ $$$$\mathrm{cos}\:\mathrm{36}°+\mathrm{cos}\:\mathrm{108}°=\: \\ $$$$\mathrm{2cos}\:\mathrm{72}°\:\mathrm{cos}\:\mathrm{36}°\:=\:\mathrm{2sin}\:\mathrm{18}°\mathrm{cos}\:\mathrm{36}° \\ $$$$=\:\mathrm{2sin}\:\mathrm{18}°\:\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{18}°\right) \\ $$$$=\:\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}−\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{1}−\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\sqrt{\mathrm{5}}+\mathrm{1}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}×\mathrm{4}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\bigstar \\ $$

Commented by OlafThorendsen last updated on 23/Jul/20

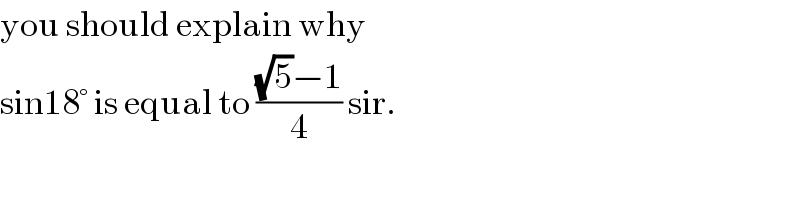
you should explain why sin18° is equal to (((√5)−1)/4) sir.

$$\mathrm{you}\:\mathrm{should}\:\mathrm{explain}\:\mathrm{why} \\ $$$$\mathrm{sin18}°\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:\mathrm{sir}. \\ $$

Commented by 6478 last updated on 23/Jul/20

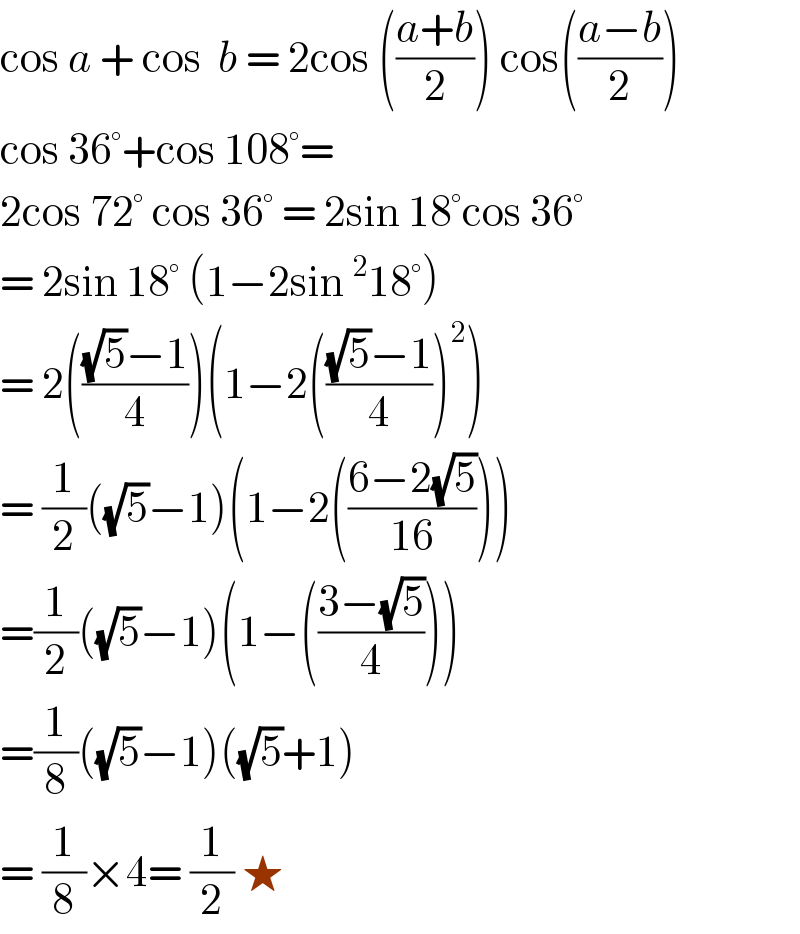
cos a + cos b = 2cos (((a+b)/2)) cos(((a−b)/2)) cos 36°+cos 108°= 2cos 72° cos 36° = 2sin 18°cos 36° = 2sin 18° (1−2sin^2 18°) = 2((((√5)−1)/4))(1−2((((√5)−1)/4))^2 ) = (1/2)((√5)−1)(1−2(((6−2(√5))/(16)))) =(1/2)((√5)−1)(1−(((3−(√5))/4))) =(1/8)((√5)−1)((√5)+1) = (1/8)×4= (1/2) ★

$$\mathrm{cos}\:{a}\:+\:\mathrm{cos}\:\:{b}\:=\:\mathrm{2cos}\:\left(\frac{{a}+{b}}{\mathrm{2}}\right)\:\mathrm{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right) \\ $$$$\mathrm{cos}\:\mathrm{36}°+\mathrm{cos}\:\mathrm{108}°=\: \\ $$$$\mathrm{2cos}\:\mathrm{72}°\:\mathrm{cos}\:\mathrm{36}°\:=\:\mathrm{2sin}\:\mathrm{18}°\mathrm{cos}\:\mathrm{36}° \\ $$$$=\:\mathrm{2sin}\:\mathrm{18}°\:\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{18}°\right) \\ $$$$=\:\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}−\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{1}−\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\sqrt{\mathrm{5}}+\mathrm{1}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}×\mathrm{4}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\bigstar \\ $$

Commented by bemath last updated on 23/Jul/20

Answered by OlafThorendsen last updated on 23/Jul/20

a = cos36° b = cos108° a+b = cos36°+cos108° = cos(π/5)+cos((3π)/5) a+b = cos(π/5)−cos((2π)/5) a+b = cos(π/5)−(2cos^2 (π/5)−1) a+b = a−2a^2 +1 (1) a+b = cos(π/5)+cos((3π)/5) a+b = 2cos((((3π)/5)+(π/5))/2)cos((((3π)/5)−(π/5))/2) a+b = 2cos((2π)/5)cos(π/5) a+b = 2(2a^2 −1)a (2) (1) and (2) : 2(2a^2 −1)a = a−2a^2 +1 4a^3 +2a^2 −3a−1 = 0 (a+1)(4a^2 −2a−1) = 0 a = cos(π/5) = −1 : impossible 4a^2 −2a−1 = 0 a = ((1±(√5))/4) a = cos(π/5) = ((1−(√5))/4)<0 : impossible Finally a = cos(π/5) = ((1+(√5))/4) Then b = cos((3π)/5) = −cos((2π)/5) = −(2a^2 −1) b = 1−2(((1+(√5))/4))^2 = ((1−(√5))/4) a+b = ((1+(√5))/4)+((1−(√5))/4) = (1/2)

$${a}\:=\:\mathrm{cos36}° \\ $$$${b}\:=\:\mathrm{cos108}° \\ $$$${a}+{b}\:=\:\mathrm{cos36}°+\mathrm{cos108}°\:=\:\mathrm{cos}\frac{\pi}{\mathrm{5}}+\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{5}} \\ $$$${a}+{b}\:=\:\mathrm{cos}\frac{\pi}{\mathrm{5}}−\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{5}} \\ $$$${a}+{b}\:=\:\mathrm{cos}\frac{\pi}{\mathrm{5}}−\left(\mathrm{2cos}^{\mathrm{2}} \frac{\pi}{\mathrm{5}}−\mathrm{1}\right) \\ $$$${a}+{b}\:=\:{a}−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\:\left(\mathrm{1}\right) \\ $$$${a}+{b}\:=\:\mathrm{cos}\frac{\pi}{\mathrm{5}}+\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{5}} \\ $$$${a}+{b}\:=\:\mathrm{2cos}\frac{\frac{\mathrm{3}\pi}{\mathrm{5}}+\frac{\pi}{\mathrm{5}}}{\mathrm{2}}\mathrm{cos}\frac{\frac{\mathrm{3}\pi}{\mathrm{5}}−\frac{\pi}{\mathrm{5}}}{\mathrm{2}} \\ $$$${a}+{b}\:=\:\mathrm{2cos}\frac{\mathrm{2}\pi}{\mathrm{5}}\mathrm{cos}\frac{\pi}{\mathrm{5}} \\ $$$${a}+{b}\:=\:\mathrm{2}\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}\right){a}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:: \\ $$$$\mathrm{2}\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}\right){a}\:=\:{a}−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{4}{a}^{\mathrm{3}} +\mathrm{2}{a}^{\mathrm{2}} −\mathrm{3}{a}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\left({a}+\mathrm{1}\right)\left(\mathrm{4}{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$${a}\:=\:\mathrm{cos}\frac{\pi}{\mathrm{5}}\:=\:−\mathrm{1}\::\:\mathrm{impossible} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{1}\:=\:\mathrm{0} \\ $$$${a}\:=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${a}\:=\:\mathrm{cos}\frac{\pi}{\mathrm{5}}\:=\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}<\mathrm{0}\::\:\mathrm{impossible} \\ $$$$\mathrm{Finally}\:{a}\:=\:\mathrm{cos}\frac{\pi}{\mathrm{5}}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{Then}\:{b}\:=\:\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{5}}\:=\:−\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{5}}\:=\:−\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${b}\:=\:\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${a}+{b}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by 1549442205PVT last updated on 23/Jul/20

36°+54°=90°⇒sin36°=cos54° ⇒2sin18°cos18°=cos3.18°=4cos^3 18°−3cos18° ⇒2sin18°=4cos^2 18°−3 ⇒2sin18°=4(1−sin^2 18°)−3 ⇔4sin^2 18°+2sin18°−1=0 ⇔(2sin18°+(1/2))^2 −(5/4)=0⇔2sin18°+(1/2)=((√5)/2) ⇒sin18°=(((√5)−1)/4)⇒cos72°=sin18°=(((√5)−1)/4) cos 72°=2co^2 36°−1=(((√5)−1)/4) ⇒cos^2 36°=((3+(√5))/8)=((6+2(√5))/(16))⇒cos36°=(((√5)+1)/4) cos108°=cos(90°+18°)=−sin18°=((1−(√5))/4) Therefore,cos36°+cos108°= ((1+(√5))/4)+((1−(√5))/4)=(1/2)

$$\mathrm{36}°+\mathrm{54}°=\mathrm{90}°\Rightarrow\mathrm{sin36}°=\mathrm{cos54}° \\ $$$$\Rightarrow\mathrm{2sin18}°\mathrm{cos18}°=\mathrm{cos3}.\mathrm{18}°=\mathrm{4cos}^{\mathrm{3}} \mathrm{18}°−\mathrm{3cos18}° \\ $$$$\Rightarrow\mathrm{2sin18}°=\mathrm{4cos}^{\mathrm{2}} \mathrm{18}°−\mathrm{3} \\ $$$$\Rightarrow\mathrm{2sin18}°=\mathrm{4}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{18}°\right)−\mathrm{3} \\ $$$$\Leftrightarrow\mathrm{4sin}^{\mathrm{2}} \mathrm{18}°+\mathrm{2sin18}°−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{2sin18}°+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}=\mathrm{0}\Leftrightarrow\mathrm{2sin18}°+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\Rightarrow\mathrm{cos72}°=\mathrm{sin18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\mathrm{72}°=\mathrm{2co}^{\mathrm{2}} \mathrm{36}°−\mathrm{1}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \mathrm{36}°=\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{8}}=\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\Rightarrow\mathrm{cos36}°=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{cos108}°=\mathrm{cos}\left(\mathrm{90}°+\mathrm{18}°\right)=−\mathrm{sin18}°=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{Therefore},\mathrm{cos36}°+\mathrm{cos108}°= \\ $$$$\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com