Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 104701 by abony1303 last updated on 23/Jul/20

Commented by abony1303 last updated on 23/Jul/20

Pls help

$$\mathrm{Pls}\:\mathrm{help} \\ $$

Answered by mathmax by abdo last updated on 23/Jul/20

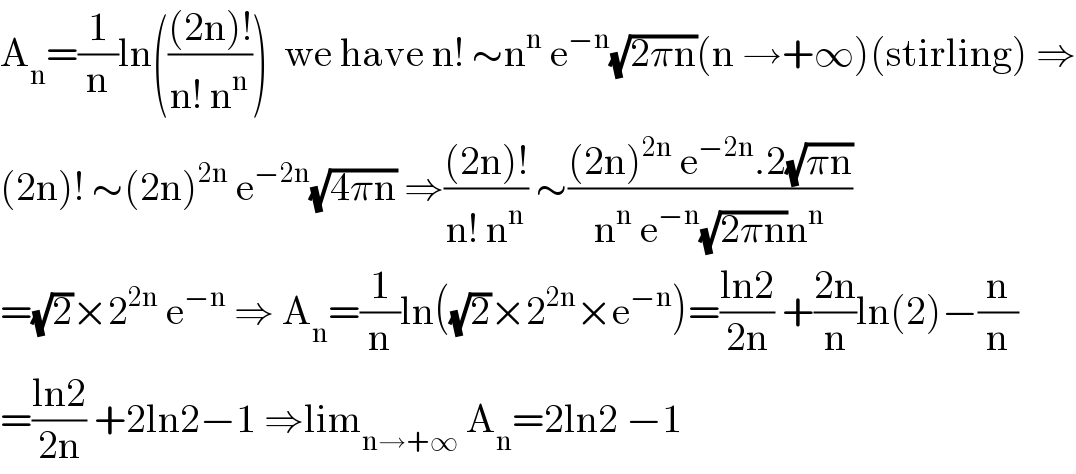
A_n =(1/n)ln((((2n)!)/(n! n^n ))) we have n! ∼n^n e^(−n) (√(2πn))(n →+∞)(stirling) ⇒ (2n)! ∼(2n)^(2n) e^(−2n) (√(4πn)) ⇒(((2n)!)/(n! n^n )) ∼(((2n)^(2n) e^(−2n) .2(√(πn)))/(n^n e^(−n) (√(2πn))n^n )) =(√2)×2^(2n) e^(−n) ⇒ A_n =(1/n)ln((√2)×2^(2n) ×e^(−n) )=((ln2)/(2n)) +((2n)/n)ln(2)−(n/n) =((ln2)/(2n)) +2ln2−1 ⇒lim_(n→+∞) A_n =2ln2 −1

$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\frac{\left(\mathrm{2n}\right)!}{\mathrm{n}!\:\mathrm{n}^{\mathrm{n}} }\right)\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{n}!\:\sim\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\left(\mathrm{n}\:\rightarrow+\infty\right)\left(\mathrm{stirling}\right)\:\Rightarrow \\ $$$$\left(\mathrm{2n}\right)!\:\sim\left(\mathrm{2n}\right)^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{2n}} \sqrt{\mathrm{4}\pi\mathrm{n}}\:\Rightarrow\frac{\left(\mathrm{2n}\right)!}{\mathrm{n}!\:\mathrm{n}^{\mathrm{n}} }\:\sim\frac{\left(\mathrm{2n}\right)^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{2n}} .\mathrm{2}\sqrt{\pi\mathrm{n}}}{\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\mathrm{n}^{\mathrm{n}} } \\ $$$$=\sqrt{\mathrm{2}}×\mathrm{2}^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{n}} \:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\sqrt{\mathrm{2}}×\mathrm{2}^{\mathrm{2n}} ×\mathrm{e}^{−\mathrm{n}} \right)=\frac{\mathrm{ln2}}{\mathrm{2n}}\:+\frac{\mathrm{2n}}{\mathrm{n}}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{n}}{\mathrm{n}} \\ $$$$=\frac{\mathrm{ln2}}{\mathrm{2n}}\:+\mathrm{2ln2}−\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{2ln2}\:−\mathrm{1} \\ $$

Commented by abony1303 last updated on 23/Jul/20

couldnt catch you ser :(

$$\mathrm{couldnt}\:\mathrm{catch}\:\mathrm{you}\:\mathrm{ser}\::\left(\right. \\ $$

Commented by mathmax by abdo last updated on 23/Jul/20

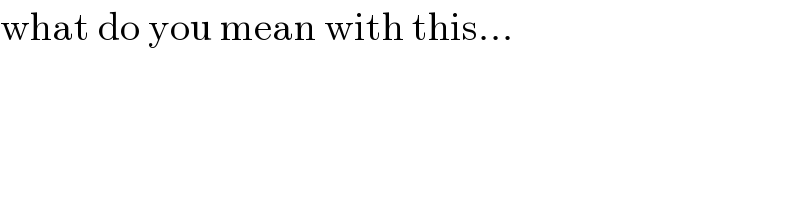
what do you mean with this...

$$\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{with}\:\mathrm{this}... \\ $$

Commented by abony1303 last updated on 23/Jul/20

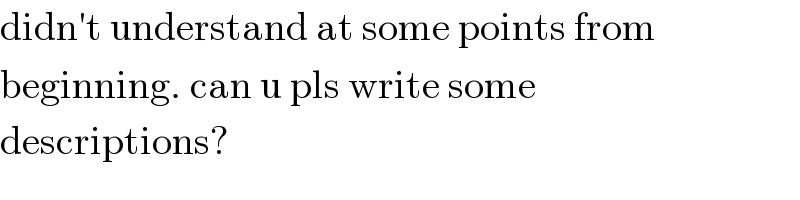
didn′t understand at some points from beginning. can u pls write some descriptions?

$$\mathrm{didn}'\mathrm{t}\:\mathrm{understand}\:\mathrm{at}\:\mathrm{some}\:\mathrm{points}\:\mathrm{from} \\ $$$$\mathrm{beginning}.\:\mathrm{can}\:\mathrm{u}\:\mathrm{pls}\:\mathrm{write}\:\mathrm{some} \\ $$$$\mathrm{descriptions}? \\ $$

Commented by abony1303 last updated on 24/Jul/20

Thank you ser. It was very helpful. Didnt′t know about Sterling′s approximation.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{ser}.\:\mathrm{It}\:\mathrm{was}\:\mathrm{very}\:\mathrm{helpful}. \\ $$$$\mathrm{Didnt}'\mathrm{t}\:\mathrm{know}\:\mathrm{about}\:\mathrm{Sterling}'\mathrm{s} \\ $$$$\mathrm{approximation}. \\ $$

Commented by mathmax by abdo last updated on 24/Jul/20

here i have used th stirling formula n! ∼ n^n e^(−n) (√(2πn)) (for n →+∞) i think the answer is clear

$$\mathrm{here}\:\mathrm{i}\:\mathrm{have}\:\mathrm{used}\:\mathrm{th}\:\mathrm{stirling}\:\mathrm{formula}\:\:\mathrm{n}!\:\sim\:\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\:\:\left(\mathrm{for}\:\mathrm{n}\:\rightarrow+\infty\right) \\ $$$$\:\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{clear}\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com