Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 104735 by bemath last updated on 23/Jul/20

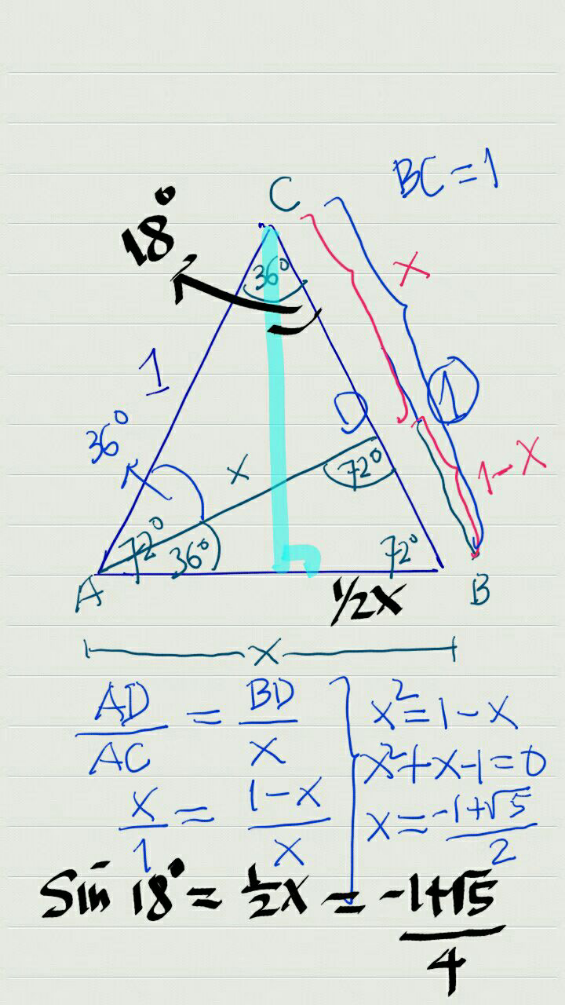
Commented by 1549442205PVT last updated on 23/Jul/20

what is your question?

$$\boldsymbol{\mathrm{what}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{question}}? \\ $$

Commented by bemath last updated on 23/Jul/20

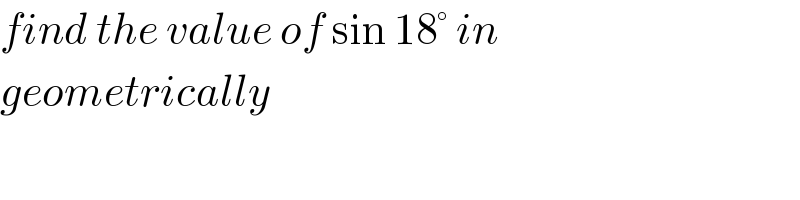
find the value of sin 18° in geometrically

$${find}\:{the}\:{value}\:{of}\:\mathrm{sin}\:\mathrm{18}°\:{in} \\ $$$${geometrically} \\ $$

Answered by 1549442205PVT last updated on 24/Jul/20

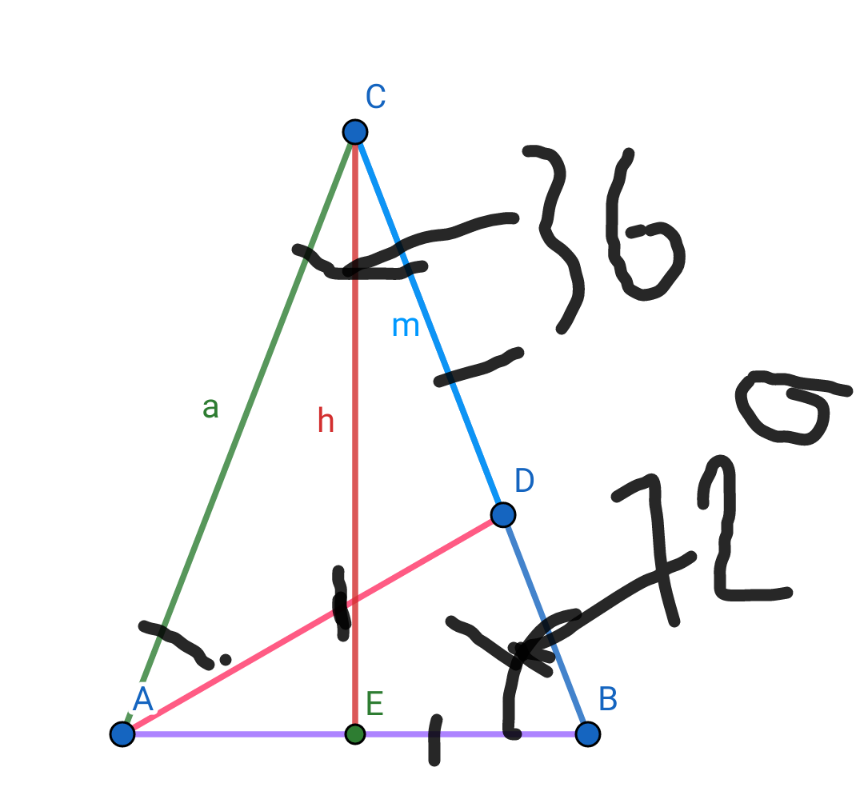
Commented by 1549442205PVT last updated on 24/Jul/20

Drawing an isosceles triamgle ABC,CA=CB=a with ACB^(�) =36°.Then CAB^(�) =CBA^(�) =72°. A point D taken on the side BC such that DA=DC=m.Denote the midpoont of side AB by E.Then we get DCA^(�) =DAC^(�) =36° ⇒DAB^(�) =72°−36°=36°⇒ADB^(�) =72°,so ΔABD is isosceles at A⇒AB=AD=m and hence ΔABD⋍ΔCAB(a.a) ⇒((AD)/(BC))=((BD)/(AB))⇔(m/a)=((a−m)/m)⇔a^2 −am−m^2 =0 This is a quadratic equation for a with (√Δ)=(√(m^2 +4m^2 ))=m(√5).Hence a=((m+m(√5))/2)=((m((√5)+1))/2). Since CE is the bisector line of ΔABC ,BCE^(�) =(1/2)ACB^(�_ ) =18° and CE⊥AB,so sin18°=sinBCE^(�) =((BE)/(BC))=(m/2):a=(m/2):((m((√5)+1))/2) =(1/((√5)+1))=((1×((√5)−1))/(((√(5+1)))((√5)−1)))=(((√5)−1)/4) Thus,sin18°=(((√5)−1)/4) which we need to find

$$\mathrm{Drawing}\:\mathrm{an}\:\mathrm{isosceles}\:\mathrm{triamgle}\:\mathrm{ABC},\mathrm{CA}=\mathrm{CB}=\mathrm{a} \\ $$$$\mathrm{with}\:\widehat {\mathrm{ACB}}=\mathrm{36}°.\mathrm{Then}\:\widehat {\mathrm{CAB}}=\widehat {\mathrm{CBA}}=\mathrm{72}°. \\ $$$$\mathrm{A}\:\mathrm{point}\:\mathrm{D}\:\mathrm{taken}\:\mathrm{on}\:\mathrm{the}\:\mathrm{side}\:\mathrm{BC}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{DA}=\mathrm{DC}=\mathrm{m}.\mathrm{Denote}\:\mathrm{the}\:\mathrm{midpoont}\:\mathrm{of}\: \\ $$$$\mathrm{side}\:\mathrm{AB}\:\mathrm{by}\:\mathrm{E}.\mathrm{Then}\:\mathrm{we}\:\mathrm{get}\:\widehat {\mathrm{DCA}}=\widehat {\mathrm{DAC}}=\mathrm{36}° \\ $$$$\Rightarrow\widehat {\mathrm{DAB}}=\mathrm{72}°−\mathrm{36}°=\mathrm{36}°\Rightarrow\widehat {\mathrm{ADB}}=\mathrm{72}°,\mathrm{so} \\ $$$$\Delta\mathrm{ABD}\:\mathrm{is}\:\mathrm{isosceles}\:\mathrm{at}\:\mathrm{A}\Rightarrow\mathrm{AB}=\mathrm{AD}=\mathrm{m} \\ $$$$\mathrm{and}\:\mathrm{hence}\:\Delta\mathrm{ABD}\backsimeq\Delta\mathrm{CAB}\left(\mathrm{a}.\mathrm{a}\right) \\ $$$$\Rightarrow\frac{\mathrm{AD}}{\mathrm{BC}}=\frac{\mathrm{BD}}{\mathrm{AB}}\Leftrightarrow\frac{\mathrm{m}}{\mathrm{a}}=\frac{\mathrm{a}−\mathrm{m}}{\mathrm{m}}\Leftrightarrow\mathrm{a}^{\mathrm{2}} −\mathrm{am}−\mathrm{m}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{a}\:\mathrm{with} \\ $$$$\sqrt{\Delta}=\sqrt{\mathrm{m}^{\mathrm{2}} +\mathrm{4m}^{\mathrm{2}} }=\mathrm{m}\sqrt{\mathrm{5}}.\mathrm{Hence} \\ $$$$\mathrm{a}=\frac{\mathrm{m}+\mathrm{m}\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{\mathrm{m}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{2}}. \\ $$$$\mathrm{Since}\:\mathrm{CE}\:\mathrm{is}\:\mathrm{the}\:\mathrm{bisector}\:\mathrm{line}\:\mathrm{of}\:\Delta\mathrm{ABC} \\ $$$$,\widehat {\mathrm{BCE}}=\frac{\mathrm{1}}{\mathrm{2}}\widehat {\mathrm{ACB}}=\mathrm{18}°\:\mathrm{and}\:\mathrm{CE}\bot\mathrm{AB},\mathrm{so} \\ $$$$\mathrm{sin18}°=\mathrm{sin}\widehat {\mathrm{BCE}}=\frac{\mathrm{BE}}{\mathrm{BC}}=\frac{\mathrm{m}}{\mathrm{2}}:\mathrm{a}=\frac{\mathrm{m}}{\mathrm{2}}:\frac{\mathrm{m}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}+\mathrm{1}}=\frac{\mathrm{1}×\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\left(\sqrt{\mathrm{5}+\mathrm{1}}\right)\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{sin}}\mathrm{18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:\:\boldsymbol{\mathrm{which}}\:\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{find}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com