
Question Number 104746 by bobhans last updated on 23/Jul/20
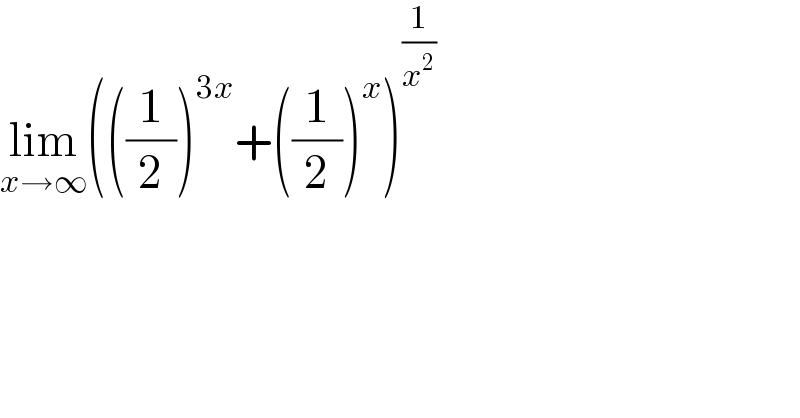
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}{x}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \: \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jul/20
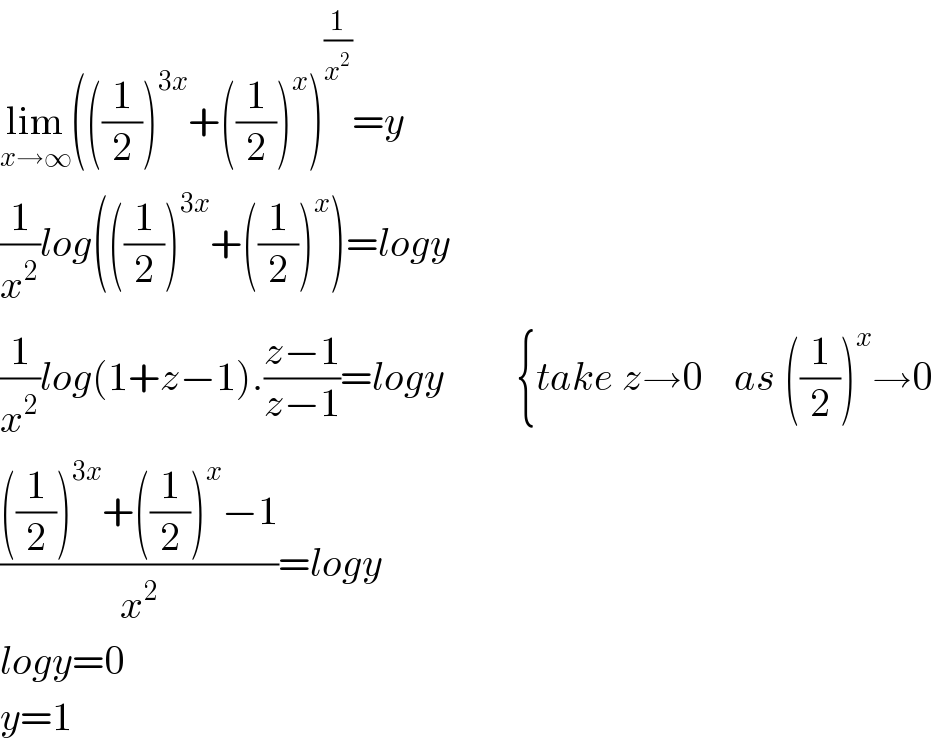
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}{x}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} ={y} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{log}\left(\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}{x}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \right)={logy} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{log}\left(\mathrm{1}+{z}−\mathrm{1}\right).\frac{{z}−\mathrm{1}}{{z}−\mathrm{1}}={logy}\:\:\:\:\:\:\:\:\:\left\{{take}\:{z}\rightarrow\mathrm{0}\:\:\:\:{as}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \rightarrow\mathrm{0}\right. \\ $$$$\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}{x}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} −\mathrm{1}}{{x}^{\mathrm{2}} }={logy} \\ $$$${logy}=\mathrm{0} \\ $$$${y}=\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 23/Jul/20
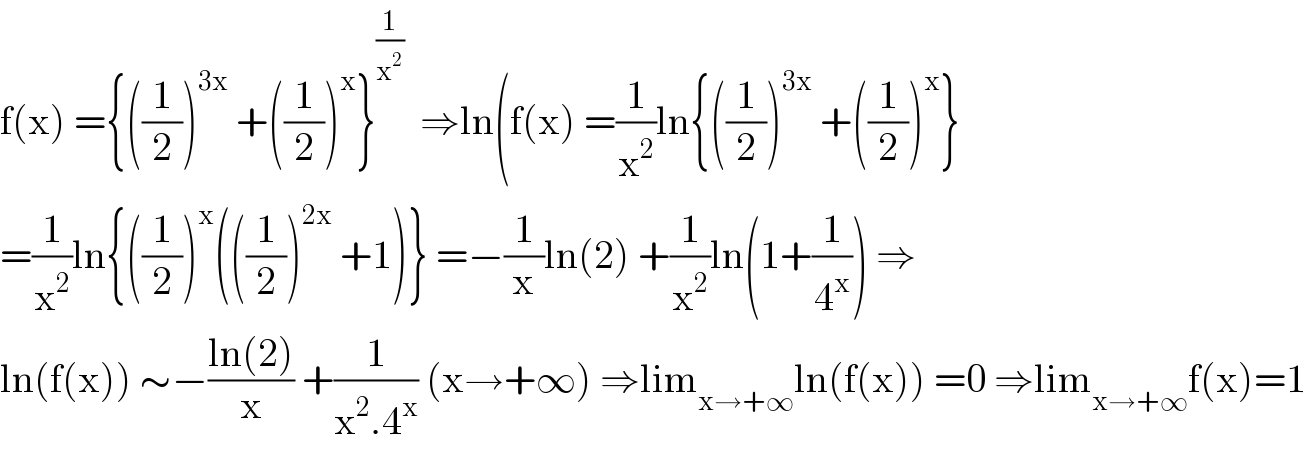
$$\mathrm{f}\left(\mathrm{x}\right)\:=\left\{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3x}} \:+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{x}} \right\}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:\:\Rightarrow\mathrm{ln}\left(\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left\{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3x}} \:+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{x}} \right\}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left\{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{x}} \left(\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2x}} \:+\mathrm{1}\right)\right\}\:=−\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{x}} }\right)\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:\sim−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{x}}\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} .\mathrm{4}^{\mathrm{x}} }\:\left(\mathrm{x}\rightarrow+\infty\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{1} \\ $$
