Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 104769 by mr W last updated on 23/Jul/20

Commented by mr W last updated on 23/Jul/20

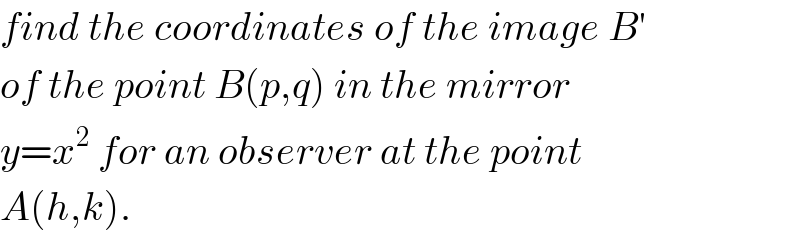
find the coordinates of the image B′ of the point B(p,q) in the mirror y=x^2 for an observer at the point A(h,k).

$${find}\:{the}\:{coordinates}\:{of}\:{the}\:{image}\:{B}'\: \\ $$$${of}\:{the}\:{point}\:{B}\left({p},{q}\right)\:{in}\:{the}\:{mirror} \\ $$$${y}={x}^{\mathrm{2}} \:{for}\:{an}\:{observer}\:{at}\:{the}\:{point} \\ $$$${A}\left({h},{k}\right). \\ $$

Answered by mr W last updated on 24/Jul/20

Commented by mr W last updated on 25/Jul/20

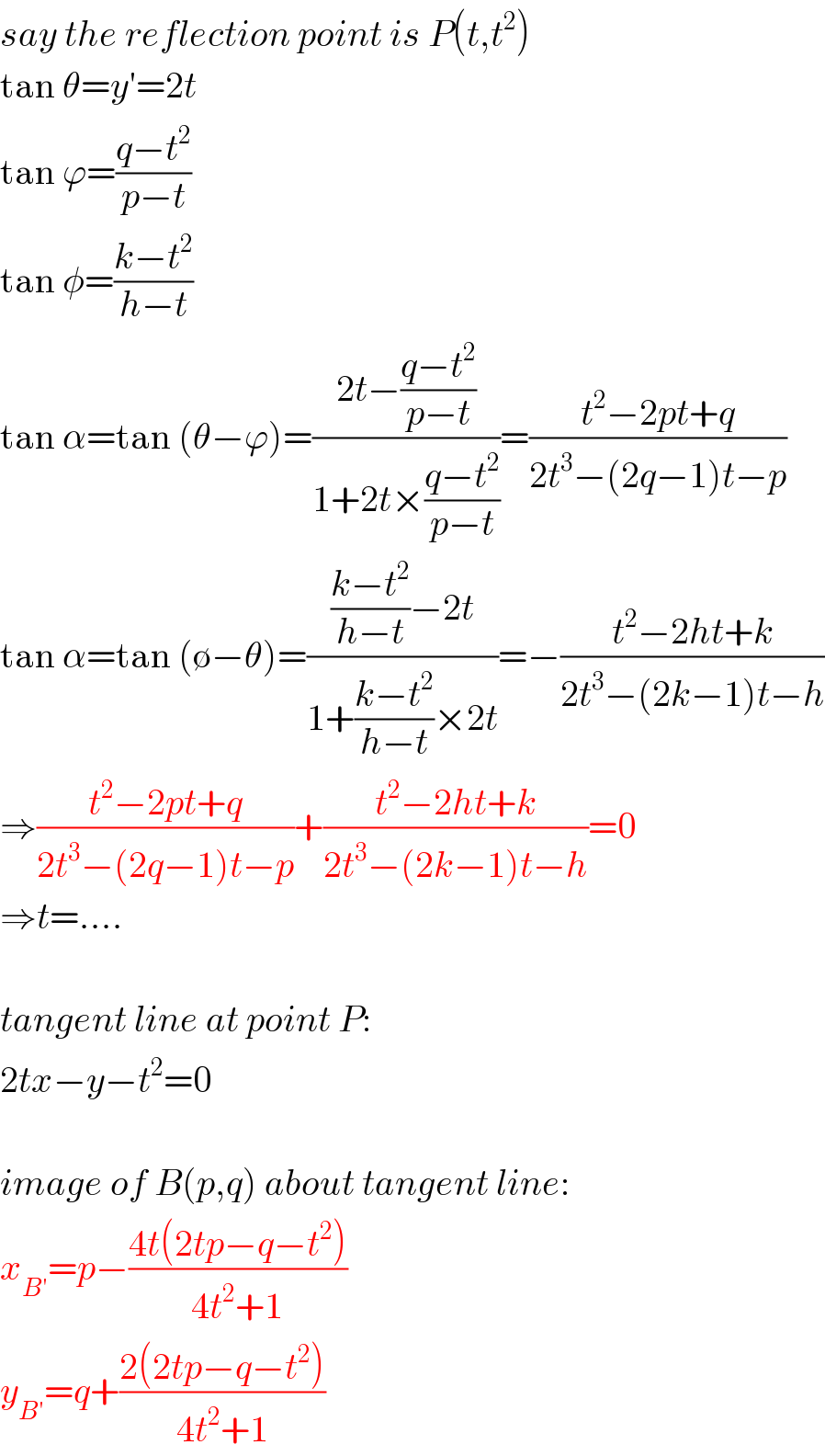
say the reflection point is P(t,t^2 ) tan θ=y′=2t tan ϕ=((q−t^2 )/(p−t)) tan φ=((k−t^2 )/(h−t)) tan α=tan (θ−ϕ)=((2t−((q−t^2 )/(p−t)))/(1+2t×((q−t^2 )/(p−t))))=((t^2 −2pt+q)/(2t^3 −(2q−1)t−p)) tan α=tan (∅−θ)=((((k−t^2 )/(h−t))−2t)/(1+((k−t^2 )/(h−t))×2t))=−((t^2 −2ht+k)/(2t^3 −(2k−1)t−h)) ⇒((t^2 −2pt+q)/(2t^3 −(2q−1)t−p))+((t^2 −2ht+k)/(2t^3 −(2k−1)t−h))=0 ⇒t=.... tangent line at point P: 2tx−y−t^2 =0 image of B(p,q) about tangent line: x_(B′) =p−((4t(2tp−q−t^2 ))/(4t^2 +1)) y_(B′) =q+((2(2tp−q−t^2 ))/(4t^2 +1))

$${say}\:{the}\:{reflection}\:{point}\:{is}\:{P}\left({t},{t}^{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{2}{t} \\ $$$$\mathrm{tan}\:\varphi=\frac{{q}−{t}^{\mathrm{2}} }{{p}−{t}} \\ $$$$\mathrm{tan}\:\phi=\frac{{k}−{t}^{\mathrm{2}} }{{h}−{t}} \\ $$$$\mathrm{tan}\:\alpha=\mathrm{tan}\:\left(\theta−\varphi\right)=\frac{\mathrm{2}{t}−\frac{{q}−{t}^{\mathrm{2}} }{{p}−{t}}}{\mathrm{1}+\mathrm{2}{t}×\frac{{q}−{t}^{\mathrm{2}} }{{p}−{t}}}=\frac{{t}^{\mathrm{2}} −\mathrm{2}{pt}+{q}}{\mathrm{2}{t}^{\mathrm{3}} −\left(\mathrm{2}{q}−\mathrm{1}\right){t}−{p}} \\ $$$$\mathrm{tan}\:\alpha=\mathrm{tan}\:\left(\emptyset−\theta\right)=\frac{\frac{{k}−{t}^{\mathrm{2}} }{{h}−{t}}−\mathrm{2}{t}}{\mathrm{1}+\frac{{k}−{t}^{\mathrm{2}} }{{h}−{t}}×\mathrm{2}{t}}=−\frac{{t}^{\mathrm{2}} −\mathrm{2}{ht}+{k}}{\mathrm{2}{t}^{\mathrm{3}} −\left(\mathrm{2}{k}−\mathrm{1}\right){t}−{h}} \\ $$$$\Rightarrow\frac{{t}^{\mathrm{2}} −\mathrm{2}{pt}+{q}}{\mathrm{2}{t}^{\mathrm{3}} −\left(\mathrm{2}{q}−\mathrm{1}\right){t}−{p}}+\frac{{t}^{\mathrm{2}} −\mathrm{2}{ht}+{k}}{\mathrm{2}{t}^{\mathrm{3}} −\left(\mathrm{2}{k}−\mathrm{1}\right){t}−{h}}=\mathrm{0} \\ $$$$\Rightarrow{t}=.... \\ $$$$ \\ $$$${tangent}\:{line}\:{at}\:{point}\:{P}: \\ $$$$\mathrm{2}{tx}−{y}−{t}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$${image}\:{of}\:{B}\left({p},{q}\right)\:{about}\:{tangent}\:{line}: \\ $$$${x}_{{B}'} ={p}−\frac{\mathrm{4}{t}\left(\mathrm{2}{tp}−{q}−{t}^{\mathrm{2}} \right)}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}_{{B}'} ={q}+\frac{\mathrm{2}\left(\mathrm{2}{tp}−{q}−{t}^{\mathrm{2}} \right)}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}} \\ $$

Commented by mr W last updated on 25/Jul/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com