Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 104772 by mathmax by abdo last updated on 23/Jul/20

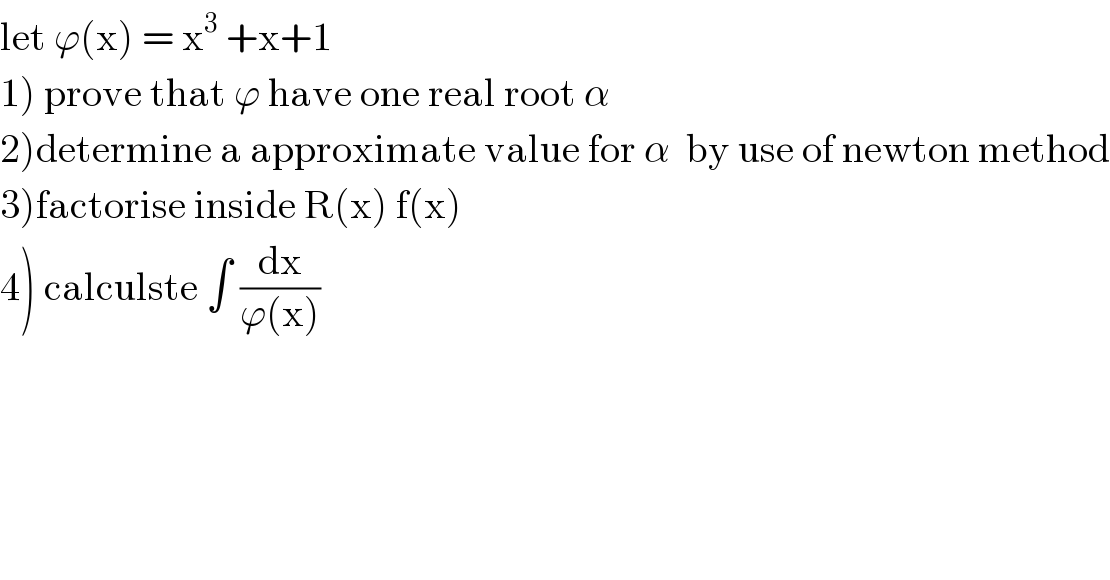
let ϕ(x) = x^3 +x+1 1) prove that ϕ have one real root α 2)determine a approximate value for α by use of newton method 3)factorise inside R(x) f(x) 4) calculste ∫ (dx/(ϕ(x)))

$$\mathrm{let}\:\varphi\left(\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{3}} \:+\mathrm{x}+\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{prove}\:\mathrm{that}\:\varphi\:\mathrm{have}\:\mathrm{one}\:\mathrm{real}\:\mathrm{root}\:\alpha \\ $$$$\left.\mathrm{2}\right)\mathrm{determine}\:\mathrm{a}\:\mathrm{approximate}\:\mathrm{value}\:\mathrm{for}\:\alpha\:\:\mathrm{by}\:\mathrm{use}\:\mathrm{of}\:\mathrm{newton}\:\mathrm{method} \\ $$$$\left.\mathrm{3}\right)\mathrm{factorise}\:\mathrm{inside}\:\mathrm{R}\left(\mathrm{x}\right)\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\left.\mathrm{4}\right)\:\mathrm{calculste}\:\int\:\frac{\mathrm{dx}}{\varphi\left(\mathrm{x}\right)} \\ $$

Answered by MAB last updated on 23/Jul/20

1) ϕ′(x)=3x^2 +1>0 lim_(x→−∞) ϕ(x)=−∞ lim_(x→+∞) ϕ(x)=+∞ hence ϕ is a bijection of ]−∞,+∞[ to itself, ϕ has a unique real root 2)x_(n+1) =x_n −((ϕ(x_n ))/(ϕ′(x_n ))) x_(n+1) =x_n −((x_n ^3 +x_n +1)/(3x_n ^2 +1)) x_(n+1) =((2x_n ^3 −1)/(3x_n ^2 −1)) let x_0 =0 using python x_5 =−0.6823278039465127 to be continued...

$$\left.\mathrm{1}\right)\:\varphi'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}>\mathrm{0}\: \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\varphi\left({x}\right)=−\infty \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\varphi\left({x}\right)=+\infty \\ $$$$\left.{hence}\:\varphi\:{is}\:{a}\:{bijection}\:{of}\:\right]−\infty,+\infty\left[\:{to}\right. \\ $$$${itself},\:\varphi\:{has}\:{a}\:{unique}\:{real}\:{root} \\ $$$$\left.\mathrm{2}\right){x}_{{n}+\mathrm{1}} ={x}_{{n}} −\frac{\varphi\left({x}_{{n}} \right)}{\varphi'\left({x}_{{n}} \right)} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} −\frac{{x}_{{n}} ^{\mathrm{3}} +{x}_{{n}} +\mathrm{1}}{\mathrm{3}{x}_{{n}} ^{\mathrm{2}} +\mathrm{1}} \\ $$$${x}_{{n}+\mathrm{1}} =\frac{\mathrm{2}{x}_{{n}} ^{\mathrm{3}} −\mathrm{1}}{\mathrm{3}{x}_{{n}} ^{\mathrm{2}} −\mathrm{1}} \\ $$$${let}\:{x}_{\mathrm{0}} =\mathrm{0} \\ $$$${using}\:{python}\:{x}_{\mathrm{5}} =−\mathrm{0}.\mathrm{6823278039465127} \\ $$$${to}\:{be}\:{continued}... \\ $$$$ \\ $$

Commented by abdomsup last updated on 23/Jul/20

thank you sir.

$${thank}\:{you}\:{sir}. \\ $$

Commented by MAB last updated on 23/Jul/20

you are welcome sir

$${you}\:{are}\:{welcome}\:{sir} \\ $$

Answered by MAB last updated on 23/Jul/20

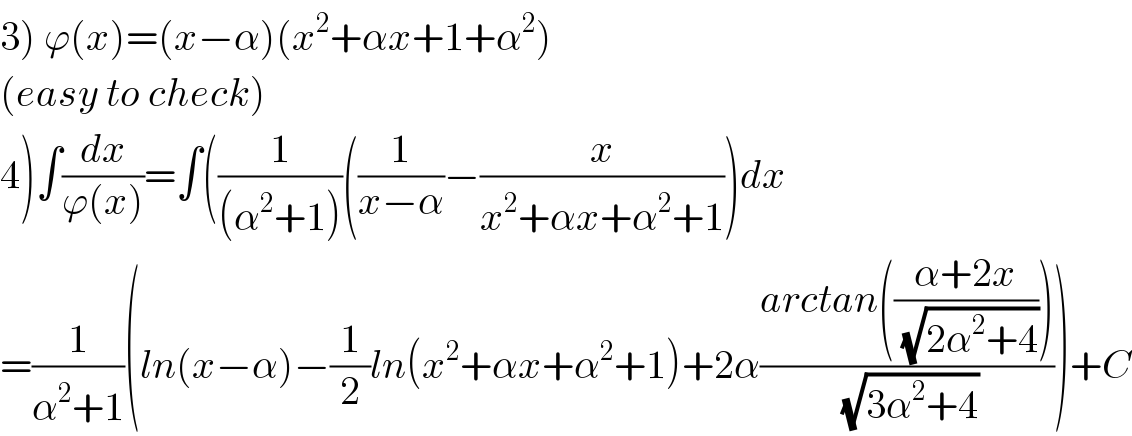
3) ϕ(x)=(x−α)(x^2 +αx+1+α^2 ) (easy to check) 4)∫(dx/(ϕ(x)))=∫((1/((α^2 +1)))((1/(x−α))−(x/(x^2 +αx+α^2 +1)))dx =(1/(α^2 +1))(ln(x−α)−(1/2)ln(x^2 +αx+α^2 +1)+2α((arctan(((α+2x)/(√(2α^2 +4)))))/(√(3α^2 +4))))+C

$$\left.\mathrm{3}\right)\:\varphi\left({x}\right)=\left({x}−\alpha\right)\left({x}^{\mathrm{2}} +\alpha{x}+\mathrm{1}+\alpha^{\mathrm{2}} \right) \\ $$$$\left({easy}\:{to}\:{check}\right) \\ $$$$\left.\mathrm{4}\right)\int\frac{{dx}}{\varphi\left({x}\right)}=\int\left(\frac{\mathrm{1}}{\left(\alpha^{\mathrm{2}} +\mathrm{1}\right)}\left(\frac{\mathrm{1}}{{x}−\alpha}−\frac{{x}}{{x}^{\mathrm{2}} +\alpha{x}+\alpha^{\mathrm{2}} +\mathrm{1}}\right){dx}\right. \\ $$$$=\frac{\mathrm{1}}{\alpha^{\mathrm{2}} +\mathrm{1}}\left({ln}\left({x}−\alpha\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +\alpha{x}+\alpha^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{2}\alpha\frac{{arctan}\left(\frac{\alpha+\mathrm{2}{x}}{\sqrt{\mathrm{2}\alpha^{\mathrm{2}} +\mathrm{4}}}\right)}{\sqrt{\mathrm{3}\alpha^{\mathrm{2}} +\mathrm{4}}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com