Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 104780 by Aziztisffola last updated on 23/Jul/20

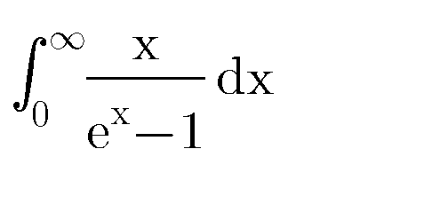
Commented by Dwaipayan Shikari last updated on 23/Jul/20

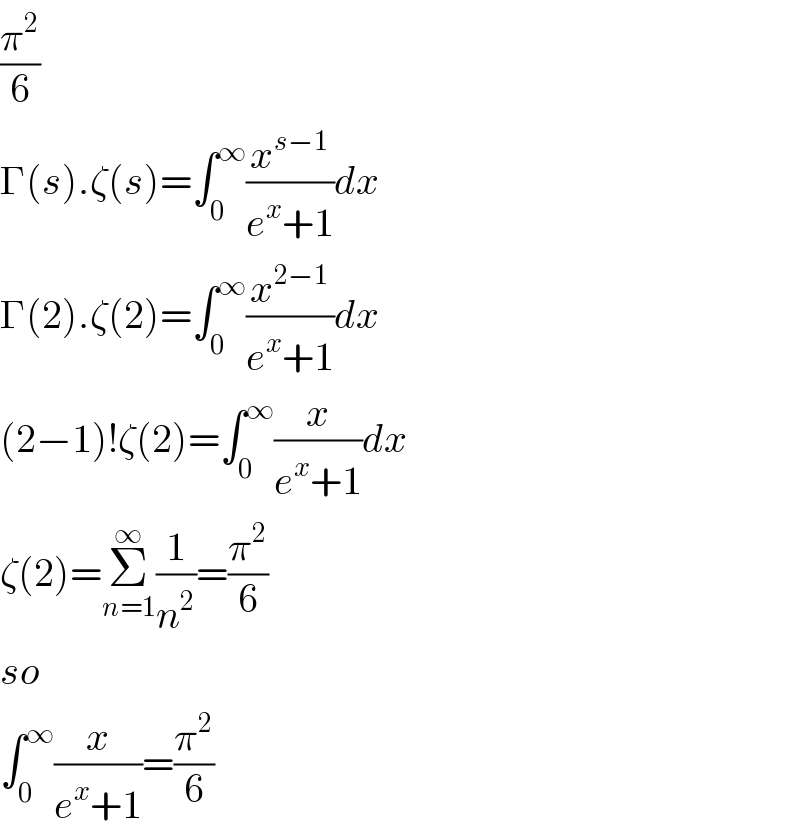
(π^2 /6) Γ(s).ζ(s)=∫_0 ^∞ (x^(s−1) /(e^x +1))dx Γ(2).ζ(2)=∫_0 ^∞ (x^(2−1) /(e^x +1))dx (2−1)!ζ(2)=∫_0 ^∞ (x/(e^x +1))dx ζ(2)=Σ_(n=1) ^∞ (1/n^2 )=(π^2 /6) so ∫_0 ^∞ (x/(e^x +1))=(π^2 /6)

$$\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\Gamma\left({s}\right).\zeta\left({s}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{s}−\mathrm{1}} }{{e}^{{x}} +\mathrm{1}}{dx} \\ $$$$\Gamma\left(\mathrm{2}\right).\zeta\left(\mathrm{2}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}−\mathrm{1}} }{{e}^{{x}} +\mathrm{1}}{dx} \\ $$$$\left(\mathrm{2}−\mathrm{1}\right)!\zeta\left(\mathrm{2}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}}{{e}^{{x}} +\mathrm{1}}{dx} \\ $$$$\zeta\left(\mathrm{2}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$${so} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}}{{e}^{{x}} +\mathrm{1}}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by Aziztisffola last updated on 23/Jul/20

Thanks sir , I found Γ(2).ζ(2)=(π^2 /6)

$$\mathrm{Thanks}\:\mathrm{sir}\:,\:\mathrm{I}\:\mathrm{found}\:\Gamma\left(\mathrm{2}\right).\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Answered by abdomsup last updated on 23/Jul/20

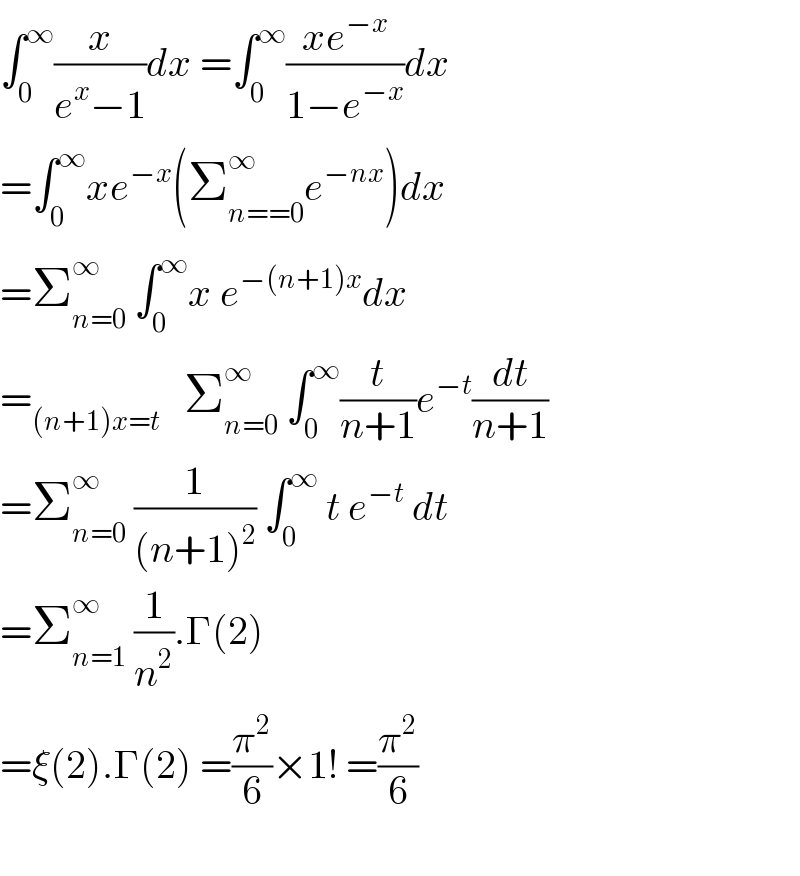
∫_0 ^∞ (x/(e^x −1))dx =∫_0 ^∞ ((xe^(−x) )/(1−e^(−x) ))dx =∫_0 ^∞ xe^(−x) (Σ_(n==0) ^∞ e^(−nx) )dx =Σ_(n=0) ^∞ ∫_0 ^∞ x e^(−(n+1)x) dx =_((n+1)x=t) Σ_(n=0) ^∞ ∫_0 ^∞ (t/(n+1))e^(−t) (dt/(n+1)) =Σ_(n=0) ^∞ (1/((n+1)^2 )) ∫_0 ^∞ t e^(−t) dt =Σ_(n=1) ^∞ (1/n^2 ).Γ(2) =ξ(2).Γ(2) =(π^2 /6)×1! =(π^2 /6)

$$\int_{\mathrm{0}} ^{\infty} \frac{{x}}{{e}^{{x}} −\mathrm{1}}{dx}\:=\int_{\mathrm{0}} ^{\infty} \frac{{xe}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {xe}^{−{x}} \left(\sum_{{n}==\mathrm{0}} ^{\infty} {e}^{−{nx}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} {x}\:{e}^{−\left({n}+\mathrm{1}\right){x}} {dx} \\ $$$$=_{\left({n}+\mathrm{1}\right){x}={t}} \:\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \frac{{t}}{{n}+\mathrm{1}}{e}^{−{t}} \frac{{dt}}{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} \:{dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }.\Gamma\left(\mathrm{2}\right) \\ $$$$=\xi\left(\mathrm{2}\right).\Gamma\left(\mathrm{2}\right)\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}×\mathrm{1}!\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$

Commented by Aziztisffola last updated on 23/Jul/20

Thanks Sir

$$\mathrm{Thanks}\:\mathrm{Sir} \\ $$

Commented by mathmax by abdo last updated on 24/Jul/20

you are welcome.

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com