Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 104783 by 175mohamed last updated on 23/Jul/20

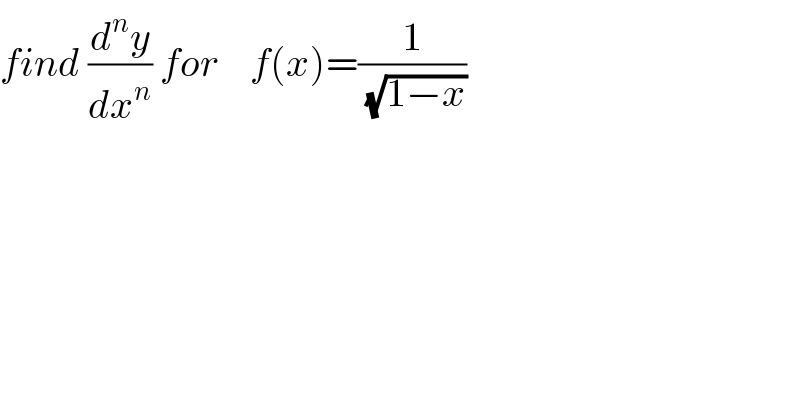
find (d^n y/dx^n ) for f(x)^ =(1/(√(1−x)))

$${find}\:\frac{{d}^{{n}} {y}}{{dx}^{{n}} }\:{for}\:\:\:\:{f}\left({x}\overset{} {\right)}=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}}} \\ $$

Answered by Dwaipayan Shikari last updated on 23/Jul/20

f(x)=(1/(√(1−x))) f^′ (x)=(1/2) (1/((1−x)^(3/2) )) f′′(x)=(3/4) (1/((1−x)^(5/2) )) f′′′(x)=((15)/8) (1/((1−x)^(7/2) )) f^( n) (x)=((Π_(n=1) ^n (2n−1))/2^n ) (1/((1−x)^(n+(1/2)) ))

$${f}\left({x}\right)=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}}} \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${f}''\left({x}\right)=\frac{\mathrm{3}}{\mathrm{4}}\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$$${f}'''\left({x}\right)=\frac{\mathrm{15}}{\mathrm{8}}\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{7}}{\mathrm{2}}} } \\ $$$${f}^{\:{n}} \left({x}\right)=\frac{\underset{{n}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{2}^{{n}} }\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$

Answered by mathmax by abdo last updated on 24/Jul/20

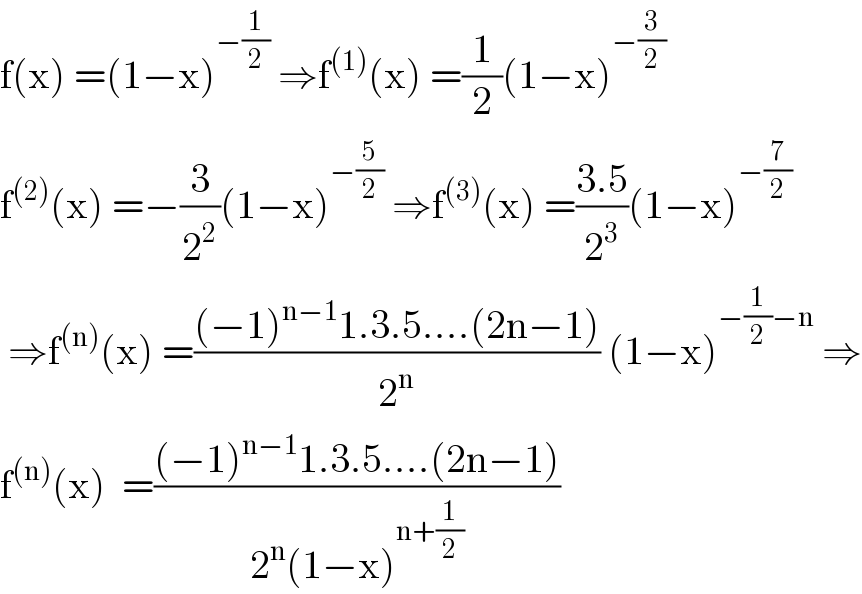
f(x) =(1−x)^(−(1/2)) ⇒f^((1)) (x) =(1/2)(1−x)^(−(3/2)) f^((2)) (x) =−(3/2^2 )(1−x)^(−(5/2)) ⇒f^((3)) (x) =((3.5)/2^3 )(1−x)^(−(7/2)) ⇒f^((n)) (x) =(((−1)^(n−1) 1.3.5....(2n−1))/2^n ) (1−x)^(−(1/2)−n) ⇒ f^((n)) (x) =(((−1)^(n−1) 1.3.5....(2n−1))/(2^n (1−x)^(n+(1/2)) ))

$$\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow\mathrm{f}^{\left(\mathrm{1}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=−\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{5}}{\mathrm{2}}} \:\Rightarrow\mathrm{f}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{3}.\mathrm{5}}{\mathrm{2}^{\mathrm{3}} }\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{7}}{\mathrm{2}}} \\ $$$$\:\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{1}.\mathrm{3}.\mathrm{5}....\left(\mathrm{2n}−\mathrm{1}\right)}{\mathrm{2}^{\mathrm{n}} }\:\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:\:=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{1}.\mathrm{3}.\mathrm{5}....\left(\mathrm{2n}−\mathrm{1}\right)}{\mathrm{2}^{\mathrm{n}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$

Commented by bubugne last updated on 24/Jul/20

why (−1)^(n−1) ?

$${why}\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:? \\ $$

Commented by abdomathmax last updated on 24/Jul/20

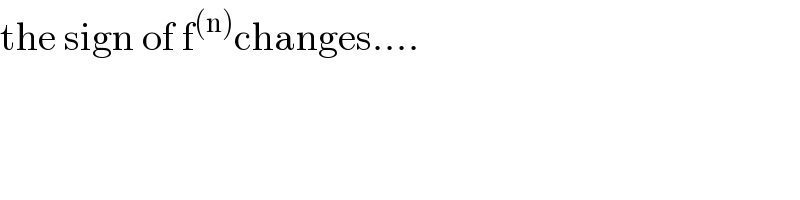
the sign of f^((n)) changes....

$$\mathrm{the}\:\mathrm{sign}\:\mathrm{of}\:\mathrm{f}^{\left(\mathrm{n}\right)} \mathrm{changes}.... \\ $$

Commented by bubugne last updated on 25/Jul/20

Does the sign of f^((n)) change? f(x)=(1−x)^(−(1/2)) ⇒ f^((1)) (x)=(−1)(−(1/2))(1−x)^(−(3/2)) f^((1)) (x)= + (1/2) (1−x)^(−(3/2)) ⇒ f^((2)) (x)= (1/2) (−1)(−(3/2))(1−x)^(−(5/2)) f^((2)) (x)= + (3/4) (1−x)^(−(5/2)) ⇒ f^((3)) (x)= (3/4) (−1)(−(5/2))(1−x)^(−(7/2)) f^((3)) (x)= + ((15)/8) (1−x)^(−(7/2)) f^((n)) (x) = + ((Π_(k=1) ^n (2k−1))/2^n ) (1−x)^(−((2n+1)/2))

$$\mathrm{Does}\:\mathrm{the}\:\mathrm{sign}\:\mathrm{of}\:\mathrm{f}^{\left(\mathrm{n}\right)} \:\mathrm{change}? \\ $$$${f}\left({x}\right)=\left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow\:{f}^{\left(\mathrm{1}\right)} \left({x}\right)=\left(−\mathrm{1}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${f}^{\left(\mathrm{1}\right)} \left({x}\right)=\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow\:{f}^{\left(\mathrm{2}\right)} \left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(−\mathrm{1}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{1}−{x}\overset{−\frac{\mathrm{5}}{\mathrm{2}}} {\right)} \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)=\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:\left(\mathrm{1}−{x}\overset{−\frac{\mathrm{5}}{\mathrm{2}}} {\right)}\Rightarrow\:{f}^{\left(\mathrm{3}\right)} \left({x}\right)=\:\frac{\mathrm{3}}{\mathrm{4}}\:\left(−\mathrm{1}\right)\left(−\frac{\mathrm{5}}{\mathrm{2}}\right)\left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{7}}{\mathrm{2}}} \\ $$$${f}^{\left(\mathrm{3}\right)} \left({x}\right)=\:+\:\frac{\mathrm{15}}{\mathrm{8}}\:\left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{7}}{\mathrm{2}}} \\ $$$${f}^{\left({n}\right)} \left({x}\right)\:=\:+\:\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{2}{k}−\mathrm{1}\right)}{\mathrm{2}^{{n}} }\:\left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com