Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 104851 by bemath last updated on 24/Jul/20

∫ ((√(x^2 −9))/x^3 ) dx

$$\int\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{{x}^{\mathrm{3}} }\:{dx}\: \\ $$

Answered by Dwaipayan Shikari last updated on 24/Jul/20

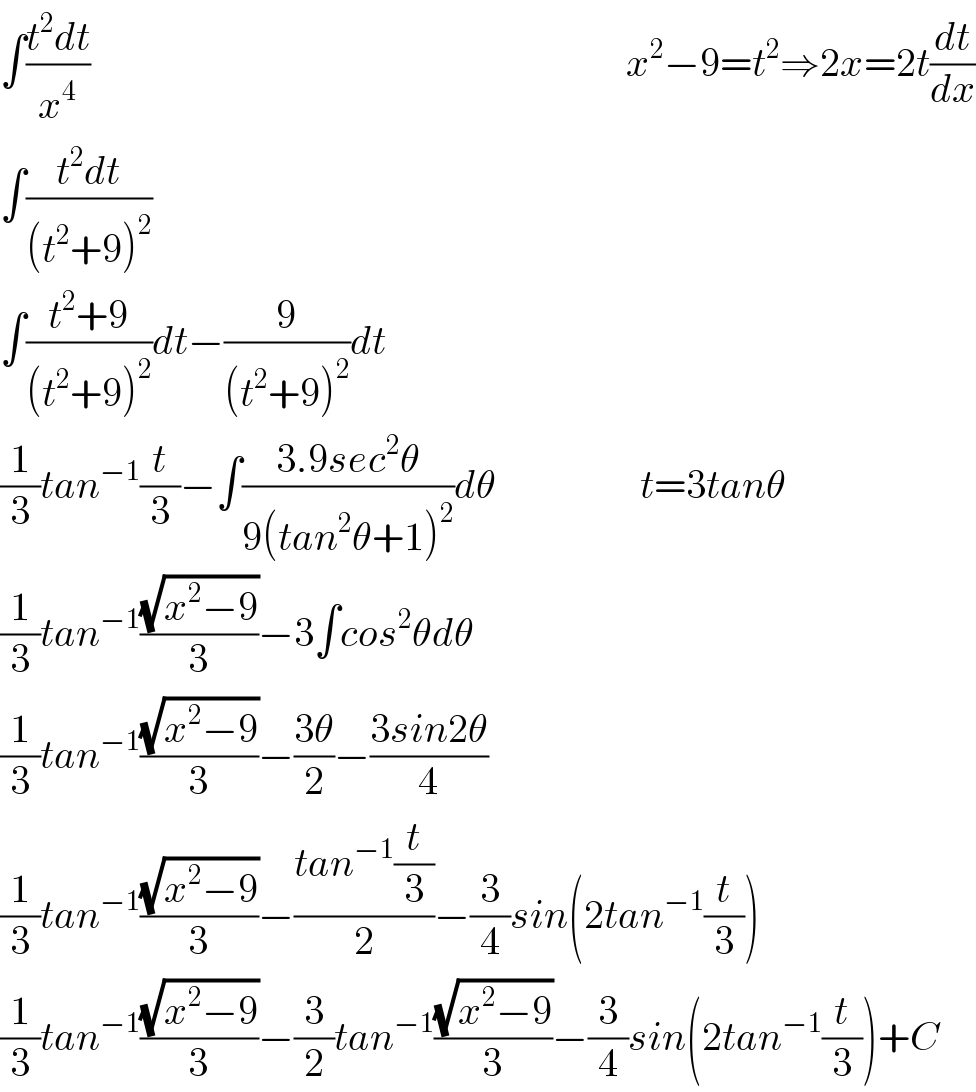
∫((t^2 dt)/x^4 ) x^2 −9=t^2 ⇒2x=2t(dt/dx) ∫((t^2 dt)/((t^2 +9)^2 )) ∫((t^2 +9)/((t^2 +9)^2 ))dt−(9/((t^2 +9)^2 ))dt (1/3)tan^(−1) (t/3)−∫((3.9sec^2 θ)/(9(tan^2 θ+1)^2 ))dθ t=3tanθ (1/3)tan^(−1) ((√(x^2 −9))/3)−3∫cos^2 θdθ (1/3)tan^(−1) ((√(x^2 −9))/3)−((3θ)/2)−((3sin2θ)/4) (1/3)tan^(−1) ((√(x^2 −9))/3)−((tan^(−1) (t/3))/2)−(3/4)sin(2tan^(−1) (t/3)) (1/3)tan^(−1) ((√(x^2 −9))/3)−(3/2)tan^(−1) ((√(x^2 −9))/3)−(3/4)sin(2tan^(−1) (t/3))+C

$$\int\frac{{t}^{\mathrm{2}} {dt}}{{x}^{\mathrm{4}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{9}={t}^{\mathrm{2}} \Rightarrow\mathrm{2}{x}=\mathrm{2}{t}\frac{{dt}}{{dx}} \\ $$$$\int\frac{{t}^{\mathrm{2}} {dt}}{\left({t}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$\int\frac{{t}^{\mathrm{2}} +\mathrm{9}}{\left({t}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }{dt}−\frac{\mathrm{9}}{\left({t}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{tan}^{−\mathrm{1}} \frac{{t}}{\mathrm{3}}−\int\frac{\mathrm{3}.\mathrm{9}{sec}^{\mathrm{2}} \theta}{\mathrm{9}\left({tan}^{\mathrm{2}} \theta+\mathrm{1}\right)^{\mathrm{2}} }{d}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}=\mathrm{3}{tan}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{tan}^{−\mathrm{1}} \frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\mathrm{3}\int{cos}^{\mathrm{2}} \theta{d}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{tan}^{−\mathrm{1}} \frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{\mathrm{3}\theta}{\mathrm{2}}−\frac{\mathrm{3}{sin}\mathrm{2}\theta}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{tan}^{−\mathrm{1}} \frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{{tan}^{−\mathrm{1}} \frac{{t}}{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}{sin}\left(\mathrm{2}{tan}^{−\mathrm{1}} \frac{{t}}{\mathrm{3}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{tan}^{−\mathrm{1}} \frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{2}}{tan}^{−\mathrm{1}} \frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{4}}{sin}\left(\mathrm{2}{tan}^{−\mathrm{1}} \frac{{t}}{\mathrm{3}}\right)+{C} \\ $$

Commented by 1549442205PVT last updated on 24/Jul/20

Sir mistaked and don′t detail at this place: −∫((9dt)/((t^2 +9)^2 ))=−∫((3.9sec^2 θdθ)/((9tan^2 θ+9)^2 ))=−(1/3)∫cos^2 θdθ −(1/3)∫cos^2 θdθ=−(1/3)∫((1+cos2θ)/2)dθ =((−θ)/6)−((sin2θ)/(12))=−(1/6)tan^(−1) (t/3)−(1/(12))×((2tanθ)/(1+tan^2 θ)) =−(1/6)tan^(−1) ((√(x^2 −9))/3)−(1/(12))×((2(t/3))/(1+(t^2 /9))) =−(1/6)tan^(−1) ((√(x^2 −9))/3)−((√(x^2 −9))/(2x^2 )) Result=(1/6)tan^(−1) ((√(x^2 −9))/3)−((√(x^2 −9))/(2x^2 ))

$$\mathrm{Sir}\:\mathrm{mistaked}\:\mathrm{and}\:\mathrm{don}'\mathrm{t}\:\mathrm{detail}\:\:\mathrm{at}\:\mathrm{this}\:\mathrm{place}: \\ $$$$−\int\frac{\mathrm{9dt}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }=−\int\frac{\mathrm{3}.\mathrm{9sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\left(\mathrm{9tan}^{\mathrm{2}} \theta+\mathrm{9}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta=−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}+\mathrm{cos2}\theta}{\mathrm{2}}\mathrm{d}\theta \\ $$$$=\frac{−\theta}{\mathrm{6}}−\frac{\mathrm{sin2}\theta}{\mathrm{12}}=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{t}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{12}}×\frac{\mathrm{2tan}\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{12}}×\frac{\mathrm{2}\frac{\mathrm{t}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{9}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{2x}^{\mathrm{2}} } \\ $$$$\boldsymbol{\mathrm{Result}}=\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \\ $$

Answered by ~blr237~ last updated on 24/Jul/20

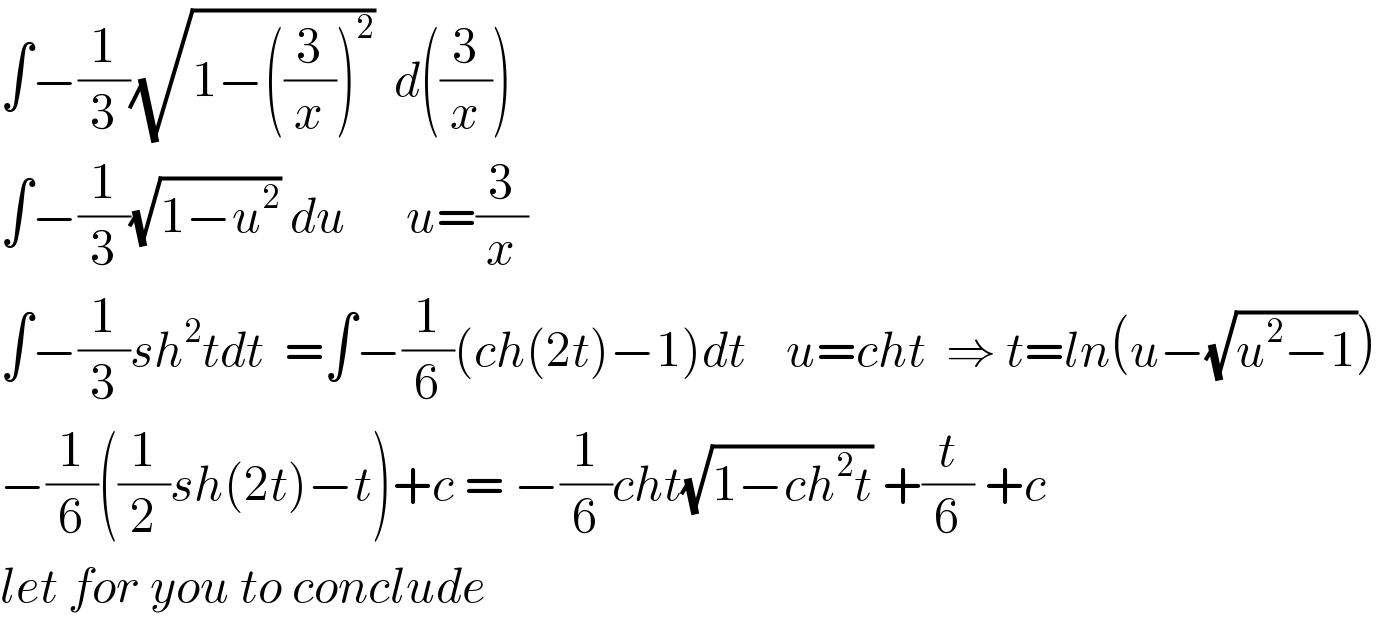
∫−(1/3)(√(1−((3/x))^2 )) d((3/x)) ∫−(1/3)(√(1−u^2 )) du u=(3/x) ∫−(1/3)sh^2 tdt =∫−(1/6)(ch(2t)−1)dt u=cht ⇒ t=ln(u−(√(u^2 −1))) −(1/6)((1/2)sh(2t)−t)+c = −(1/6)cht(√(1−ch^2 t)) +(t/6) +c let for you to conclude

$$\int−\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{1}−\left(\frac{\mathrm{3}}{{x}}\right)^{\mathrm{2}} }\:\:{d}\left(\frac{\mathrm{3}}{{x}}\right) \\ $$$$\int−\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }\:{du}\:\:\:\:\:\:{u}=\frac{\mathrm{3}}{{x}}\:\: \\ $$$$\int−\frac{\mathrm{1}}{\mathrm{3}}{sh}^{\mathrm{2}} {tdt}\:\:=\int−\frac{\mathrm{1}}{\mathrm{6}}\left({ch}\left(\mathrm{2}{t}\right)−\mathrm{1}\right){dt}\:\:\:\:{u}={cht}\:\:\Rightarrow\:{t}={ln}\left({u}−\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{2}{t}\right)−{t}\right)+{c}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}{cht}\sqrt{\mathrm{1}−{ch}^{\mathrm{2}} {t}}\:+\frac{{t}}{\mathrm{6}}\:+{c} \\ $$$${let}\:{for}\:{you}\:{to}\:{conclude} \\ $$

Commented by 1549442205PVT last updated on 25/Jul/20

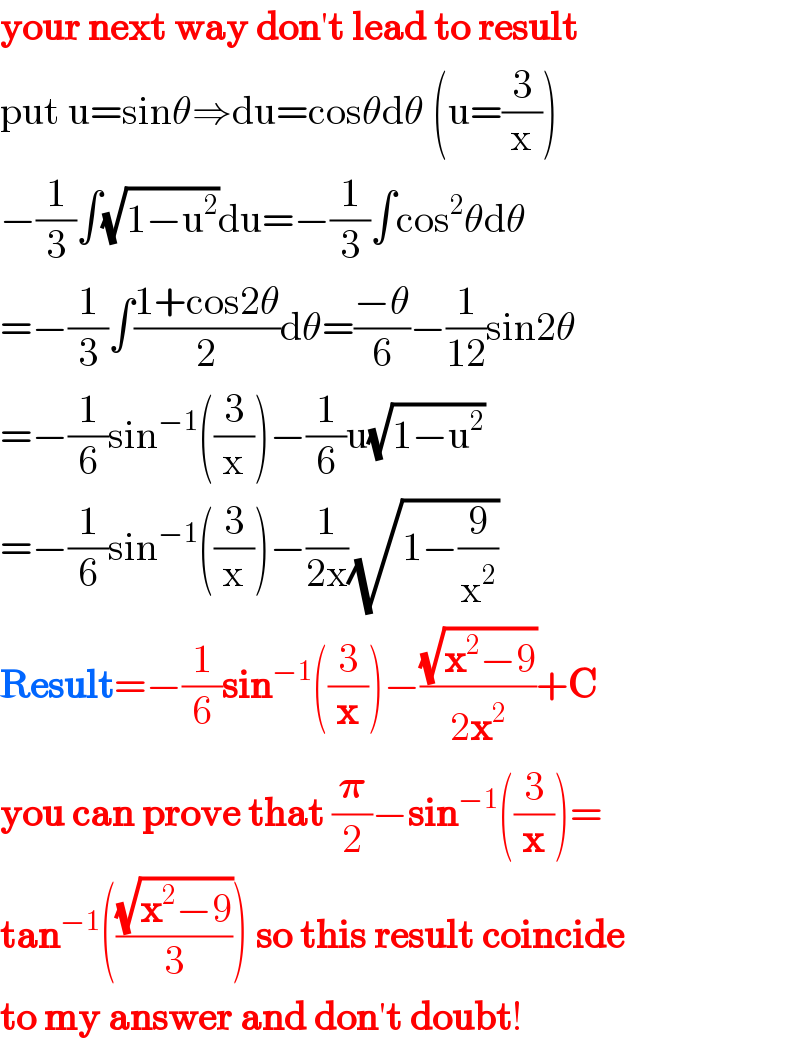
your next way don′t lead to result put u=sinθ⇒du=cosθdθ (u=(3/x)) −(1/3)∫(√(1−u^2 ))du=−(1/3)∫cos^2 θdθ =−(1/3)∫((1+cos2θ)/2)dθ=((−θ)/6)−(1/(12))sin2θ =−(1/6)sin^(−1) ((3/x))−(1/6)u(√(1−u^2 )) =−(1/6)sin^(−1) ((3/x))−(1/(2x))(√(1−(9/x^2 ))) Result=−(1/6)sin^(−1) ((3/x))−((√(x^2 −9))/(2x^2 ))+C you can prove that (𝛑/2)−sin^(−1) ((3/x))= tan^(−1) (((√(x^2 −9))/3)) so this result coincide to my answer and don′t doubt!

$$\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{next}}\:\boldsymbol{\mathrm{way}}\:\boldsymbol{\mathrm{don}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{lead}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{result}} \\ $$$$\mathrm{put}\:\mathrm{u}=\mathrm{sin}\theta\Rightarrow\mathrm{du}=\mathrm{cos}\theta\mathrm{d}\theta\:\left(\mathrm{u}=\frac{\mathrm{3}}{\mathrm{x}}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\int\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\mathrm{du}=−\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}+\mathrm{cos2}\theta}{\mathrm{2}}\mathrm{d}\theta=\frac{−\theta}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{sin2}\theta \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{u}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{2x}}\sqrt{\mathrm{1}−\frac{\mathrm{9}}{\mathrm{x}^{\mathrm{2}} }} \\ $$$$\boldsymbol{\mathrm{Result}}=−\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{\mathrm{sin}}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\boldsymbol{\mathrm{x}}}\right)−\frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }+\boldsymbol{\mathrm{C}} \\ $$$$\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:\frac{\boldsymbol{\pi}}{\mathrm{2}}−\boldsymbol{\mathrm{sin}}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\boldsymbol{\mathrm{x}}}\right)= \\ $$$$\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}\right)\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{result}}\:\boldsymbol{\mathrm{coincide}}\: \\ $$$$\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{don}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{doubt}}! \\ $$

Answered by bramlex last updated on 24/Jul/20

∫ ((x(√(1−(9/x^2 ))))/x^3 ) dx = ∫ ((√(1−(9/x^2 )))/x^2 ) dx ∫−(√(1−(9/x^2 ))) d((1/x)) [ let (1/x) = v ] ∫−(√(1−9v^2 )) dv = −{((3v)/2)(√(1−9v^2 )) +(1/2)sin^(−1) (3v)}+c =−(3/(2x))(√(1−(9/x^2 ) ))−(1/2)sin^(−1) ((3/x))+C =−(3/2)(√(x^2 −9))−(1/2)sin^(−1) ((3/x))+C

$$\int\:\frac{{x}\sqrt{\mathrm{1}−\frac{\mathrm{9}}{{x}^{\mathrm{2}} }}}{{x}^{\mathrm{3}} }\:{dx}\:=\:\int\:\frac{\sqrt{\mathrm{1}−\frac{\mathrm{9}}{{x}^{\mathrm{2}} }}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$$\int−\sqrt{\mathrm{1}−\frac{\mathrm{9}}{{x}^{\mathrm{2}} }}\:{d}\left(\frac{\mathrm{1}}{{x}}\right)\:\left[\:{let}\:\frac{\mathrm{1}}{{x}}\:=\:{v}\:\right] \\ $$$$\int−\sqrt{\mathrm{1}−\mathrm{9}{v}^{\mathrm{2}} }\:{dv}\:=\:−\left\{\frac{\mathrm{3}{v}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{9}{v}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{3}{v}\right)\right\}+{c} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}{x}}\sqrt{\mathrm{1}−\frac{\mathrm{9}}{{x}^{\mathrm{2}} }\:}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{{x}}\right)+{C} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{{x}}\right)+{C} \\ $$

Commented by 1549442205PVT last updated on 25/Jul/20

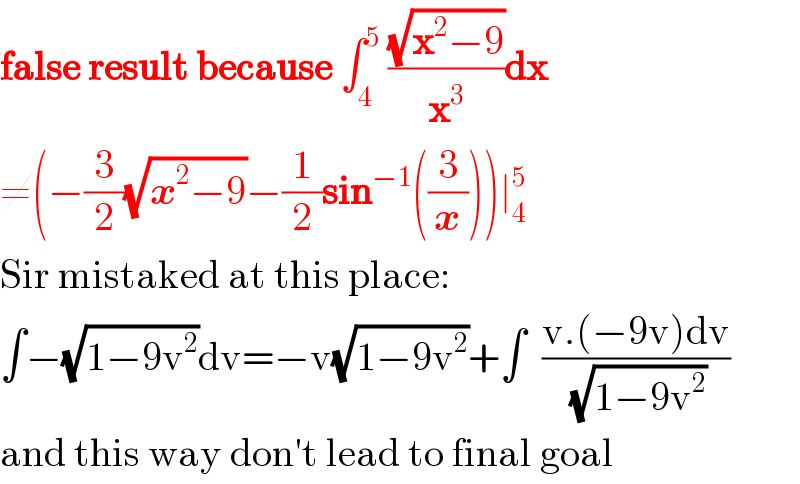
false result because ∫_4 ^5 ((√(x^2 −9))/x^3 )dx ≠(−(3/2)(√(x^2 −9))−(1/2)sin^(−1) ((3/x)))∣_4 ^5 Sir mistaked at this place: ∫−(√(1−9v^2 ))dv=−v(√(1−9v^2 ))+∫ ((v.(−9v)dv)/(√(1−9v^2 ))) and this way don′t lead to final goal

$$\boldsymbol{\mathrm{false}}\:\boldsymbol{\mathrm{result}}\:\boldsymbol{\mathrm{because}}\:\int_{\mathrm{4}} ^{\mathrm{5}} \:\frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{9}}}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} }\boldsymbol{\mathrm{dx}} \\ $$$$\neq\left(−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{sin}}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\boldsymbol{{x}}}\right)\right)\mid_{\mathrm{4}} ^{\mathrm{5}} \\ $$$$\mathrm{Sir}\:\mathrm{mistaked}\:\mathrm{at}\:\mathrm{this}\:\mathrm{place}: \\ $$$$\int−\sqrt{\mathrm{1}−\mathrm{9v}^{\mathrm{2}} }\mathrm{dv}=−\mathrm{v}\sqrt{\mathrm{1}−\mathrm{9v}^{\mathrm{2}} }+\int\:\:\frac{\mathrm{v}.\left(−\mathrm{9v}\right)\mathrm{dv}}{\sqrt{\mathrm{1}−\mathrm{9v}^{\mathrm{2}} }} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{way}\:\mathrm{don}'\mathrm{t}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{final}\:\mathrm{goal} \\ $$

Answered by 1549442205PVT last updated on 24/Jul/20

Putting (√(x^2 −9))=u⇒u^2 =x^2 −9,x=(√(u^2 +9)) ⇒udu=xdx⇒((√(x^2 −9))/x^3 )dx=((u^2 du)/((u^2 +9)^2 )) F=∫(([(u^2 +9)−9]du)/((u^2 +9)^2 ))=∫(du/(u^2 +9))−9∫(du/((u^2 +9)^2 )) =(1/3)tan^(−1) (u/3)−9I_2 Apply current formular: I_n =∫(dx/((t^2 +a^2 )))=(1/(2a^2 (n−1))).(t/((t^2 +a^2 )^(n−1) ))+(1/a^2 ).((2n−3)/(2n−2)).I_(n−1) we get I_2 =(1/(18(2−1))).(u/((u^2 +9)^(2−1) ))+(1/9).((2.2−3)/(2.2−2)).I_1 =(u/(18(u^2 +9)))+(1/(18)).∫(du/((u^2 +9))) =(u/(18(u^2 +9)))+(1/(18))×(1/3)tan^(−1) (u/3).Hence, F=(1/3)tan^(−1) (u/3)−((u/(2(u^2 +9)))+(1/6)tan^(−1) (u/3))+C =(1/6)tan^(−1) (u/3)−(u/(2(u^2 +9)))+C F=(1/6)tan^(−1) ((√(x^2 −9))/3)−((√(x^2 −9))/(2x^2 ))+C

$$\mathrm{Putting}\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}=\mathrm{u}\Rightarrow\mathrm{u}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\mathrm{9},\mathrm{x}=\sqrt{\mathrm{u}^{\mathrm{2}} +\mathrm{9}} \\ $$$$\Rightarrow\mathrm{udu}=\mathrm{xdx}\Rightarrow\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{x}^{\mathrm{3}} }\mathrm{dx}=\frac{\mathrm{u}^{\mathrm{2}} \mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$\mathrm{F}=\int\frac{\left[\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)−\mathrm{9}\right]\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }=\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{9}}−\mathrm{9}\int\frac{\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{u}}{\mathrm{3}}−\mathrm{9I}_{\mathrm{2}} \\ $$$$\mathrm{Apply}\:\mathrm{current}\:\mathrm{formular}: \\ $$$$\mathrm{I}_{\mathrm{n}} =\int\frac{\mathrm{dx}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)}.\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }.\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{2n}−\mathrm{2}}.\mathrm{I}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{18}\left(\mathrm{2}−\mathrm{1}\right)}.\frac{\mathrm{u}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{9}}.\frac{\mathrm{2}.\mathrm{2}−\mathrm{3}}{\mathrm{2}.\mathrm{2}−\mathrm{2}}.\mathrm{I}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{u}}{\mathrm{18}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)}+\frac{\mathrm{1}}{\mathrm{18}}.\int\frac{\mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$$=\frac{\mathrm{u}}{\mathrm{18}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)}+\frac{\mathrm{1}}{\mathrm{18}}×\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{u}}{\mathrm{3}}.\mathrm{Hence}, \\ $$$$\mathrm{F}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{u}}{\mathrm{3}}−\left(\frac{\mathrm{u}}{\mathrm{2}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)}+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{u}}{\mathrm{3}}\right)+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{u}}{\mathrm{3}}−\frac{\mathrm{u}}{\mathrm{2}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{9}\right)}+\mathrm{C} \\ $$$$\boldsymbol{\mathrm{F}}=\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{3}}−\frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }+\boldsymbol{\mathrm{C}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com