Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 104856 by ~blr237~ last updated on 24/Jul/20

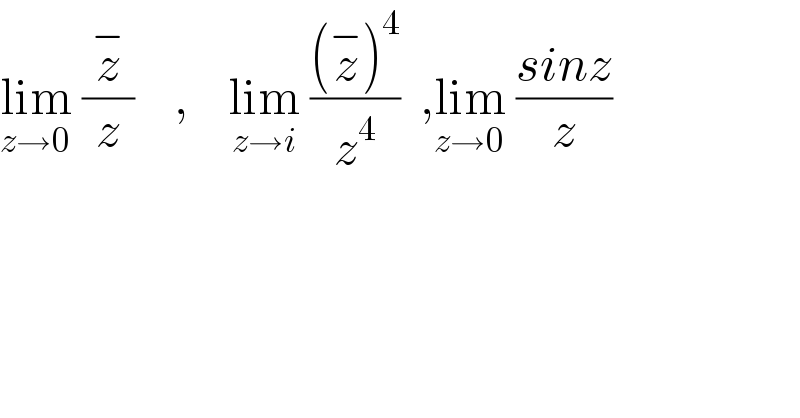
lim_(z→0) (z^− /z) , lim_(z→i) (((z^− )^4 )/z^4 ) ,lim_(z→0) ((sinz)/z)

$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\overset{−} {{z}}}{{z}}\:\:\:\:,\:\:\:\:\underset{{z}\rightarrow{i}} {\mathrm{lim}}\:\frac{\left(\overset{−} {{z}}\right)^{\mathrm{4}} }{{z}^{\mathrm{4}} }\:\:,\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{sinz}}{{z}}\: \\ $$

Answered by abdomathmax last updated on 24/Jul/20

z =r e^(iθ) z →0 ⇒r→0 lim_(z→o) (z^− /z) =lim_(r→0) ((re^(−iθ) )/(r e^(iθ) )) =lim_(r→0) e^(−2iθ) =e^(−2iθ) but this limit is not unique ⇒the limit dont exist lim_(z→i) (((z^− )^4 )/z^4 ) =(((−i)^4 )/i^4 ) =(−1)^4 =1 we have sinz =Σ_(n=0) ^∞ (((−1)^n z^(2n+1) )/((2n+1)!)) ⇒ ((sinz)/z) =Σ_(n=0) ^∞ (((−1)^n z^(2n) )/((2n+1)!)) =1−(z^2 /(2!)) +(z^4 /(5!)) −... ⇒ lim_(z→0) ((sinz)/z) =1

$$\mathrm{z}\:=\mathrm{r}\:\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{z}\:\rightarrow\mathrm{0}\:\Rightarrow\mathrm{r}\rightarrow\mathrm{0} \\ $$$$\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{o}} \:\frac{\overset{−} {\mathrm{z}}}{\mathrm{z}}\:=\mathrm{lim}_{\mathrm{r}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{re}^{−\mathrm{i}\theta} }{\mathrm{r}\:\mathrm{e}^{\mathrm{i}\theta} }\:=\mathrm{lim}_{\mathrm{r}\rightarrow\mathrm{0}} \:\:\mathrm{e}^{−\mathrm{2i}\theta} \\ $$$$=\mathrm{e}^{−\mathrm{2i}\theta} \:\:\mathrm{but}\:\mathrm{this}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{not}\:\mathrm{unique}\:\Rightarrow\mathrm{the}\:\mathrm{limit} \\ $$$$\mathrm{dont}\:\mathrm{exist} \\ $$$$\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\left(\overset{−} {\mathrm{z}}\right)^{\mathrm{4}} }{\mathrm{z}^{\mathrm{4}} }\:=\frac{\left(−\mathrm{i}\right)^{\mathrm{4}} }{\mathrm{i}^{\mathrm{4}} }\:=\left(−\mathrm{1}\right)^{\mathrm{4}} \:=\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{sinz}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{z}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\Rightarrow \\ $$$$\frac{\mathrm{sinz}}{\mathrm{z}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{z}^{\mathrm{2n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:=\mathrm{1}−\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{2}!}\:+\frac{\mathrm{z}^{\mathrm{4}} }{\mathrm{5}!}\:−...\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{sinz}}{\mathrm{z}}\:=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com