Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 104859 by qwertyu last updated on 24/Jul/20

Answered by Dwaipayan Shikari last updated on 24/Jul/20

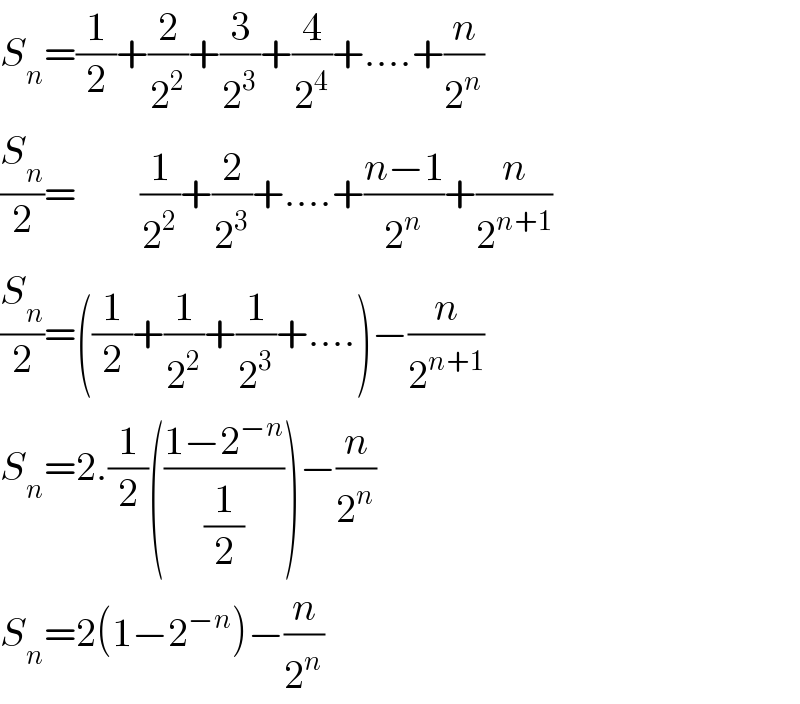
S_n =(1/2)+(2/2^2 )+(3/2^3 )+(4/2^4 )+....+(n/2^n ) (S_n /2)= (1/2^2 )+(2/2^3 )+....+((n−1)/2^n )+(n/2^(n+1) ) (S_n /2)=((1/2)+(1/2^2 )+(1/2^3 )+....)−(n/2^(n+1) ) S_n =2.(1/2)(((1−2^(−n) )/(1/2)))−(n/2^n ) S_n =2(1−2^(−n) )−(n/2^n )

$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{4}} }+....+\frac{{n}}{\mathrm{2}^{{n}} } \\ $$$$\frac{{S}_{{n}} }{\mathrm{2}}=\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{3}} }+....+\frac{{n}−\mathrm{1}}{\mathrm{2}^{{n}} }+\frac{{n}}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\frac{{S}_{{n}} }{\mathrm{2}}=\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+....\right)−\frac{{n}}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${S}_{{n}} =\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}−\mathrm{2}^{−{n}} }{\frac{\mathrm{1}}{\mathrm{2}}}\right)−\frac{{n}}{\mathrm{2}^{{n}} } \\ $$$${S}_{{n}} =\mathrm{2}\left(\mathrm{1}−\mathrm{2}^{−{n}} \right)−\frac{{n}}{\mathrm{2}^{{n}} } \\ $$

Commented by Dwaipayan Shikari last updated on 24/Jul/20

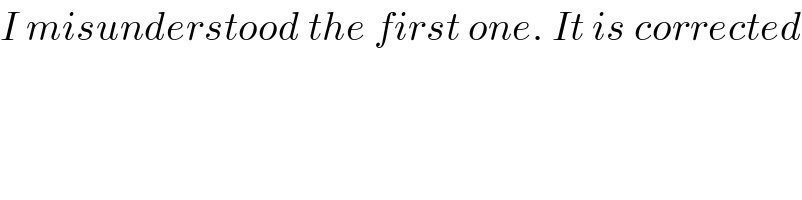
I misunderstood the first one. It is corrected

$${I}\:{misunderstood}\:{the}\:{first}\:{one}.\:{It}\:{is}\:{corrected} \\ $$

Answered by abdomathmax last updated on 26/Jul/20

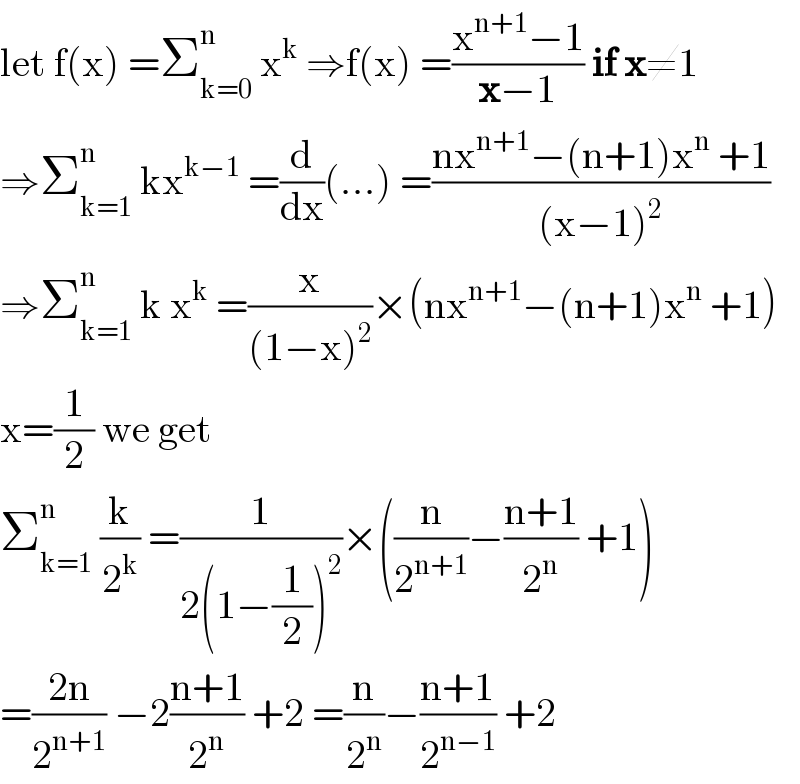
let f(x) =Σ_(k=0) ^n x^k ⇒f(x) =((x^(n+1) −1)/(x−1)) if x≠1 ⇒Σ_(k=1) ^n kx^(k−1) =(d/dx)(...) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒Σ_(k=1) ^n k x^k =(x/((1−x)^2 ))×(nx^(n+1) −(n+1)x^n +1) x=(1/2) we get Σ_(k=1) ^n (k/2^k ) =(1/(2(1−(1/2))^2 ))×((n/2^(n+1) )−((n+1)/2^n ) +1) =((2n)/2^(n+1) ) −2((n+1)/2^n ) +2 =(n/2^n )−((n+1)/2^(n−1) ) +2

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{x}^{\mathrm{k}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\boldsymbol{\mathrm{x}}−\mathrm{1}}\:\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{x}}\neq\mathrm{1} \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}−\mathrm{1}} \:=\frac{\mathrm{d}}{\mathrm{dx}}\left(...\right)\:=\frac{\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\:\mathrm{x}^{\mathrm{k}} \:=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }×\left(\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{1}\right) \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{k}}{\mathrm{2}^{\mathrm{k}} }\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }×\left(\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2n}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\:−\mathrm{2}\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:+\mathrm{2}\:=\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} }−\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}^{\mathrm{n}−\mathrm{1}} }\:+\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com