Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 10487 by Saham last updated on 13/Feb/17

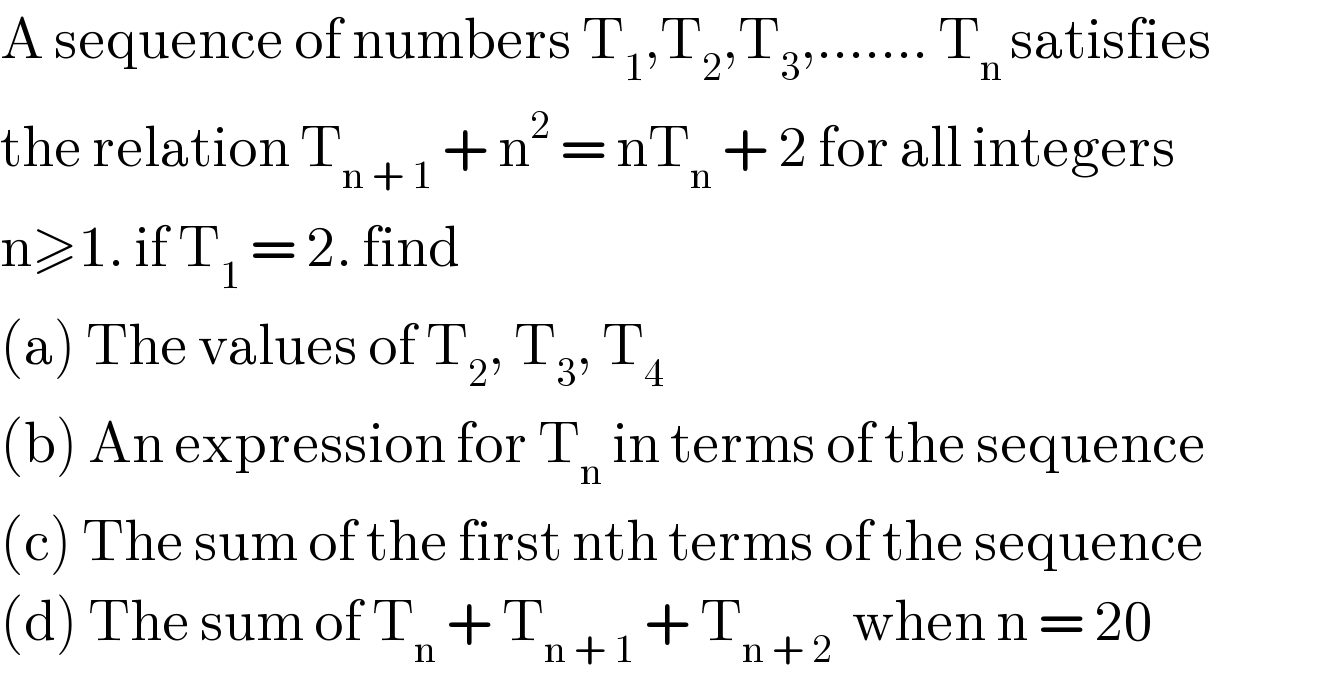
A sequence of numbers T_1 ,T_2 ,T_3 ,....... T_(n ) satisfies the relation T_(n + 1) + n^2 = nT_n + 2 for all integers n≥1. if T_1 = 2. find (a) The values of T_2 , T_3 , T_4 (b) An expression for T_n in terms of the sequence (c) The sum of the first nth terms of the sequence (d) The sum of T_n + T_(n + 1) + T_(n + 2) when n = 20

$$\mathrm{A}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{numbers}\:\mathrm{T}_{\mathrm{1}} ,\mathrm{T}_{\mathrm{2}} ,\mathrm{T}_{\mathrm{3}} ,.......\:\mathrm{T}_{\mathrm{n}\:} \mathrm{satisfies} \\ $$$$\mathrm{the}\:\mathrm{relation}\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{1}} \:+\:\mathrm{n}^{\mathrm{2}} \:=\:\mathrm{nT}_{\mathrm{n}} \:+\:\mathrm{2}\:\mathrm{for}\:\mathrm{all}\:\mathrm{integers} \\ $$$$\mathrm{n}\geqslant\mathrm{1}.\:\mathrm{if}\:\mathrm{T}_{\mathrm{1}} \:=\:\mathrm{2}.\:\mathrm{find}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{The}\:\mathrm{values}\:\mathrm{of}\:\mathrm{T}_{\mathrm{2}} ,\:\mathrm{T}_{\mathrm{3}} ,\:\mathrm{T}_{\mathrm{4}} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{An}\:\mathrm{expression}\:\mathrm{for}\:\mathrm{T}_{\mathrm{n}} \:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sequence} \\ $$$$\left(\mathrm{c}\right)\:\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{nth}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sequence} \\ $$$$\left(\mathrm{d}\right)\:\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{T}_{\mathrm{n}} \:+\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{1}} \:+\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{2}} \:\:\mathrm{when}\:\mathrm{n}\:=\:\mathrm{20} \\ $$

Answered by mrW1 last updated on 17/Feb/17

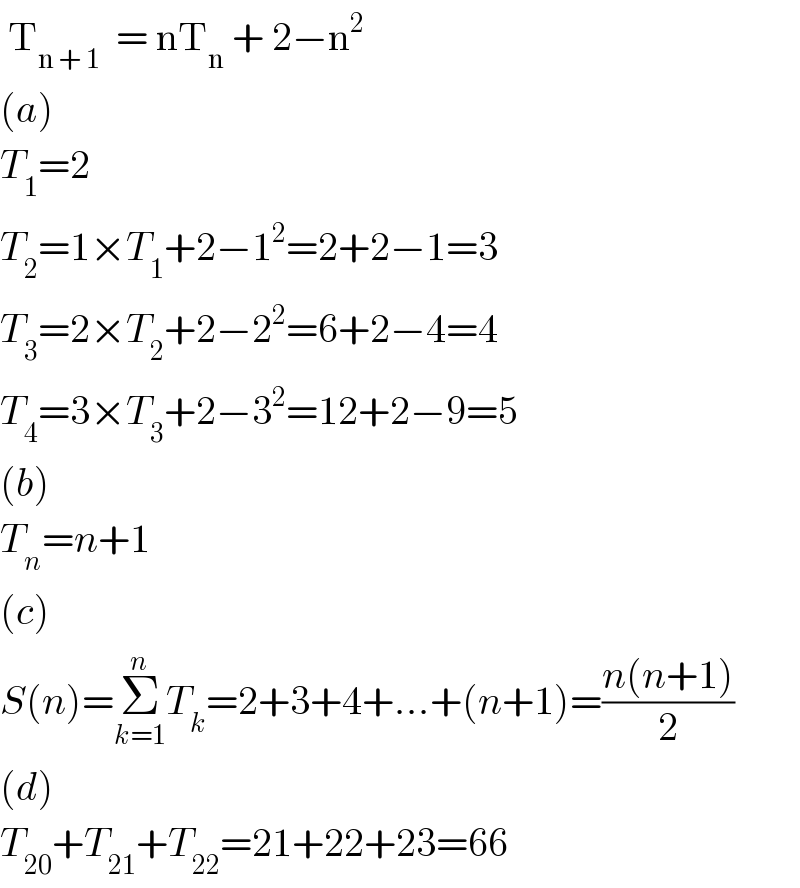
T_(n + 1) = nT_n + 2−n^2 (a) T_1 =2 T_2 =1×T_1 +2−1^2 =2+2−1=3 T_3 =2×T_2 +2−2^2 =6+2−4=4 T_4 =3×T_3 +2−3^2 =12+2−9=5 (b) T_n =n+1 (c) S(n)=Σ_(k=1) ^n T_k =2+3+4+...+(n+1)=((n(n+1))/2) (d) T_(20) +T_(21) +T_(22) =21+22+23=66

$$\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{1}} \:\:=\:\mathrm{nT}_{\mathrm{n}} \:+\:\mathrm{2}−\mathrm{n}^{\mathrm{2}} \\ $$$$\left({a}\right) \\ $$$${T}_{\mathrm{1}} =\mathrm{2} \\ $$$${T}_{\mathrm{2}} =\mathrm{1}×{T}_{\mathrm{1}} +\mathrm{2}−\mathrm{1}^{\mathrm{2}} =\mathrm{2}+\mathrm{2}−\mathrm{1}=\mathrm{3} \\ $$$${T}_{\mathrm{3}} =\mathrm{2}×{T}_{\mathrm{2}} +\mathrm{2}−\mathrm{2}^{\mathrm{2}} =\mathrm{6}+\mathrm{2}−\mathrm{4}=\mathrm{4} \\ $$$${T}_{\mathrm{4}} =\mathrm{3}×{T}_{\mathrm{3}} +\mathrm{2}−\mathrm{3}^{\mathrm{2}} =\mathrm{12}+\mathrm{2}−\mathrm{9}=\mathrm{5} \\ $$$$\left({b}\right) \\ $$$${T}_{{n}} ={n}+\mathrm{1} \\ $$$$\left({c}\right) \\ $$$${S}\left({n}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{T}_{{k}} =\mathrm{2}+\mathrm{3}+\mathrm{4}+...+\left({n}+\mathrm{1}\right)=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\left({d}\right) \\ $$$${T}_{\mathrm{20}} +{T}_{\mathrm{21}} +{T}_{\mathrm{22}} =\mathrm{21}+\mathrm{22}+\mathrm{23}=\mathrm{66} \\ $$

Commented by Saham last updated on 18/Feb/17

I really appreciate sir.

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com