(d^2 y/dx^2 ) + tan x (dy/dx) = sec x + cot x


Question and Answers Forum

All Questions Topic List
Differential Equation Questions
Previous in All Question Next in All Question
Previous in Differential Equation Next in Differential Equation
Question Number 104893 by bramlex last updated on 24/Jul/20

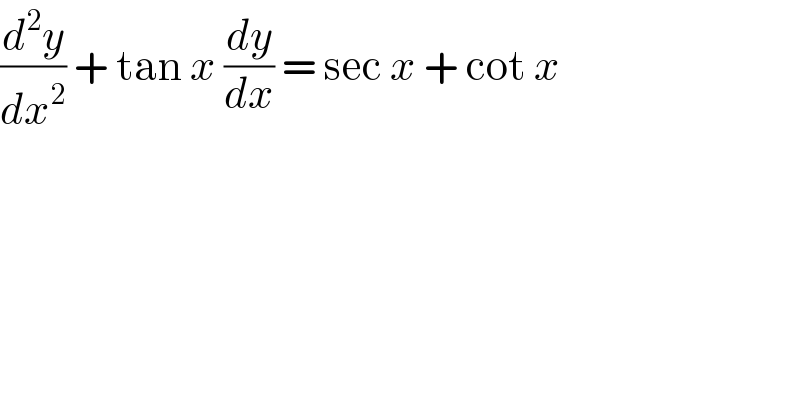
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{tan}\:{x}\:\frac{{dy}}{{dx}}\:=\:\mathrm{sec}\:{x}\:+\:\mathrm{cot}\:{x} \\ $$
	Answered by mathmax by abdo last updated on 24/Jul/20
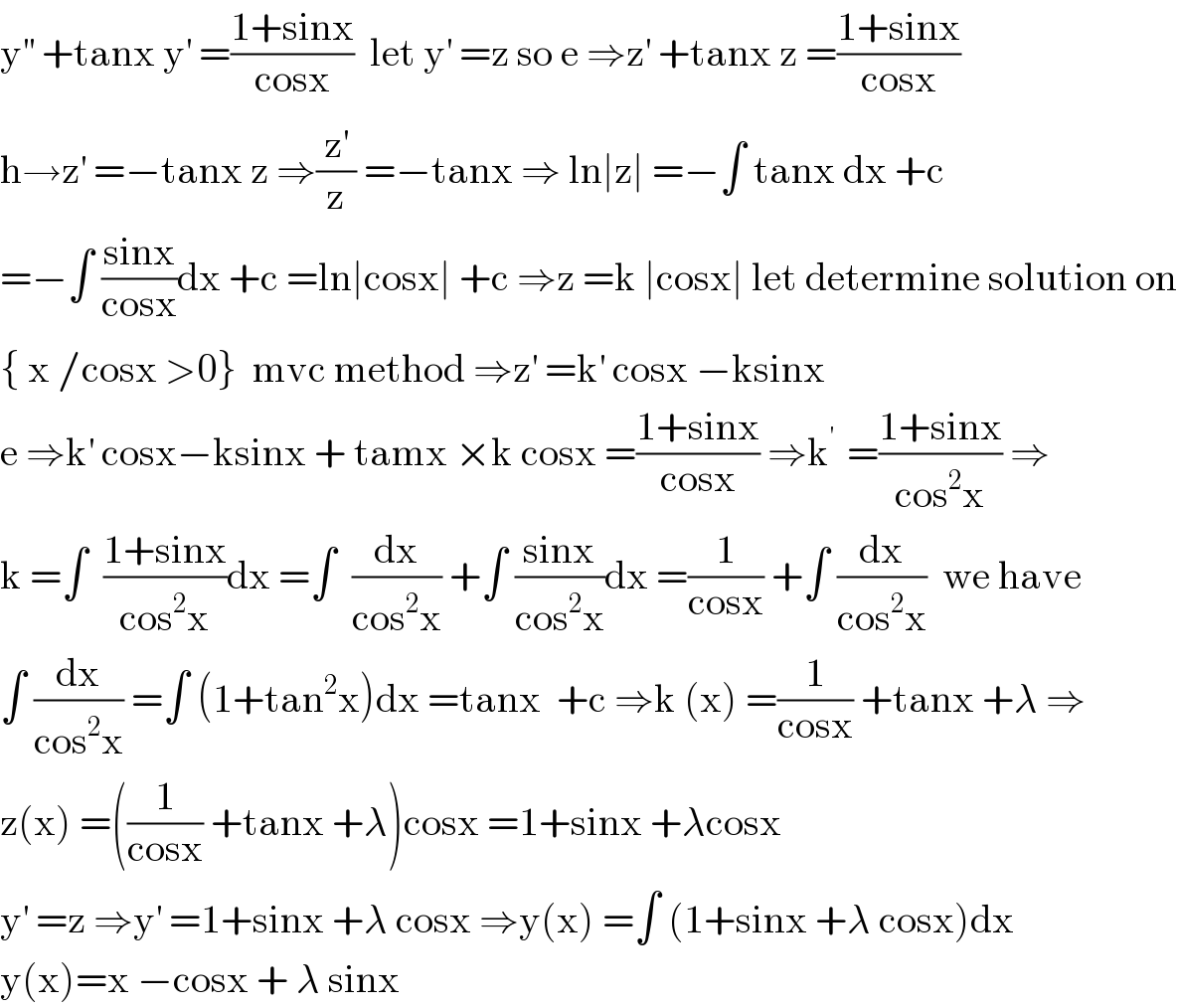
	$y^(′′) +tanx y^′ =((1+sinx)/(cosx)) let y^′ =z so e ⇒z^′ +tanx z =((1+sinx)/(cosx)) h→z^′ =−tanx z ⇒(z^′ /z) =−tanx ⇒ ln∣z∣ =−∫ tanx dx +c =−∫ ((sinx)/(cosx))dx +c =ln∣cosx∣ +c ⇒z =k ∣cosx∣ let determine solution on { x /cosx >0} mvc method ⇒z^′ =k^′ cosx −ksinx e ⇒k^′ cosx−ksinx + tamx ×k cosx =((1+sinx)/(cosx)) ⇒k^(′ ) =((1+sinx)/(cos^2 x)) ⇒ k =∫ ((1+sinx)/(cos^2 x))dx =∫ (dx/(cos^2 x)) +∫ ((sinx)/(cos^2 x))dx =(1/(cosx)) +∫ (dx/(cos^2 x)) we have ∫ (dx/(cos^2 x)) =∫ (1+tan^2 x)dx =tanx +c ⇒k (x) =(1/(cosx)) +tanx +λ ⇒ z(x) =((1/(cosx)) +tanx +λ)cosx =1+sinx +λcosx y^′ =z ⇒y^′ =1+sinx +λ cosx ⇒y(x) =∫ (1+sinx +λ cosx)dx y(x)=x −cosx + λ sinx$
	$$\mathrm{y}^{''} \:+\mathrm{tanx}\:\mathrm{y}^{'} \:=\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{cosx}}\:\:\mathrm{let}\:\mathrm{y}^{'} \:=\mathrm{z}\:\mathrm{so}\:\mathrm{e}\:\Rightarrow\mathrm{z}^{'} \:+\mathrm{tanx}\:\mathrm{z}\:=\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{cosx}} \\ $$$$\mathrm{h}\rightarrow\mathrm{z}^{'} \:=−\mathrm{tanx}\:\mathrm{z}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}\:=−\mathrm{tanx}\:\Rightarrow\:\mathrm{ln}\mid\mathrm{z}\mid\:=−\int\:\mathrm{tanx}\:\mathrm{dx}\:+\mathrm{c} \\ $$$$=−\int\:\frac{\mathrm{sinx}}{\mathrm{cosx}}\mathrm{dx}\:+\mathrm{c}\:=\mathrm{ln}\mid\mathrm{cosx}\mid\:+\mathrm{c}\:\Rightarrow\mathrm{z}\:=\mathrm{k}\:\mid\mathrm{cosx}\mid\:\mathrm{let}\:\mathrm{determine}\:\mathrm{solution}\:\mathrm{on} \\ $$$$\left\{\:\mathrm{x}\:/\mathrm{cosx}\:>\mathrm{0}\right\}\:\:\mathrm{mvc}\:\mathrm{method}\:\Rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{cosx}\:−\mathrm{ksinx} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \:\mathrm{cosx}−\mathrm{ksinx}\:+\:\mathrm{tamx}\:×\mathrm{k}\:\mathrm{cosx}\:=\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{cosx}}\:\Rightarrow\mathrm{k}^{'\:} \:=\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{k}\:=\int\:\:\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:+\int\:\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{cosx}}\:+\int\:\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:=\int\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\:=\mathrm{tanx}\:\:+\mathrm{c}\:\Rightarrow\mathrm{k}\:\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{cosx}}\:+\mathrm{tanx}\:+\lambda\:\Rightarrow \\ $$$$\mathrm{z}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{cosx}}\:+\mathrm{tanx}\:+\lambda\right)\mathrm{cosx}\:=\mathrm{1}+\mathrm{sinx}\:+\lambda\mathrm{cosx} \\ $$$$\mathrm{y}^{'} \:=\mathrm{z}\:\Rightarrow\mathrm{y}^{'} \:=\mathrm{1}+\mathrm{sinx}\:+\lambda\:\mathrm{cosx}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\int\:\left(\mathrm{1}+\mathrm{sinx}\:+\lambda\:\mathrm{cosx}\right)\mathrm{dx} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{x}\:−\mathrm{cosx}\:+\:\lambda\:\mathrm{sinx} \\ $$
	Commented by mathmax by abdo last updated on 24/Jul/20

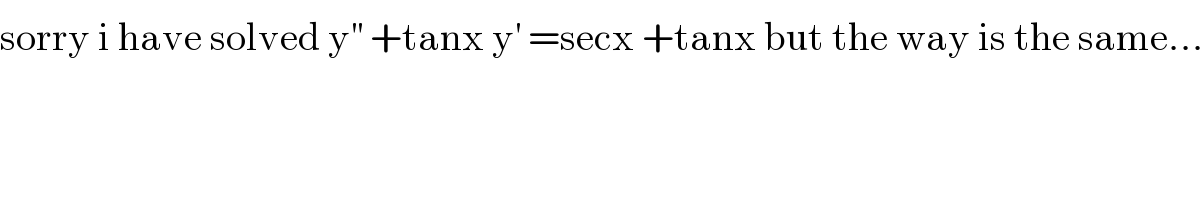
	$$\mathrm{sorry}\:\mathrm{i}\:\mathrm{have}\:\mathrm{solved}\:\mathrm{y}^{''} \:+\mathrm{tanx}\:\mathrm{y}^{'} \:=\mathrm{secx}\:+\mathrm{tanx}\:\mathrm{but}\:\mathrm{the}\:\mathrm{way}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}... \\ $$
	Commented by bramlex last updated on 24/Jul/20

	$${ok}\:{sir}\:.\:{thank}\:{you} \\ $$
	Commented by mathmax by abdo last updated on 24/Jul/20

	$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum