Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 104904 by bemath last updated on 24/Jul/20

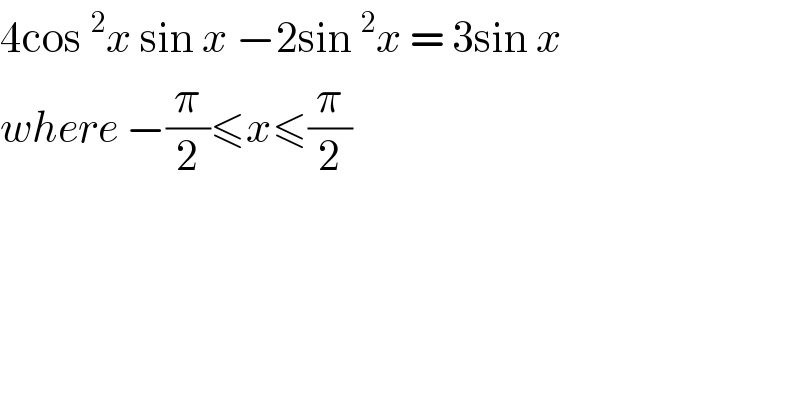
4cos^2 x sin x −2sin^2 x = 3sin x where −(π/2)≤x≤(π/2)

$$\mathrm{4cos}\:^{\mathrm{2}} {x}\:\mathrm{sin}\:{x}\:−\mathrm{2sin}\:^{\mathrm{2}} {x}\:=\:\mathrm{3sin}\:{x} \\ $$$${where}\:−\frac{\pi}{\mathrm{2}}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}} \\ $$

Answered by bramlex last updated on 24/Jul/20

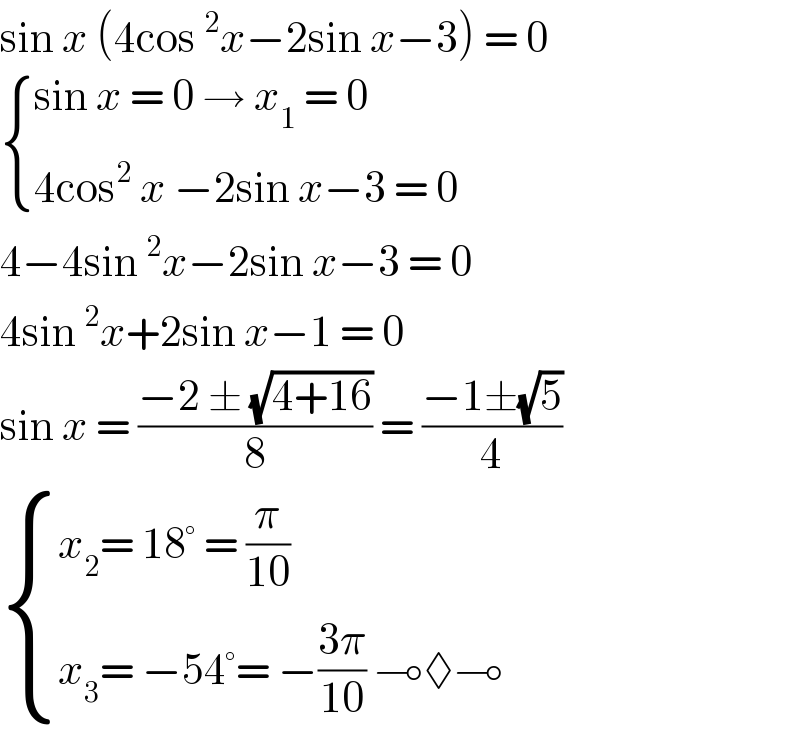
sin x (4cos^2 x−2sin x−3) = 0 { ((sin x = 0 → x_1 = 0)),((4cos^2 x −2sin x−3 = 0)) :} 4−4sin^2 x−2sin x−3 = 0 4sin^2 x+2sin x−1 = 0 sin x = ((−2 ± (√(4+16)))/8) = ((−1±(√5))/4) { ((x_2 = 18° = (π/(10)))),((x_3 = −54°= −((3π)/(10)) ⊸◊⊸)) :}

$$\mathrm{sin}\:{x}\:\left(\mathrm{4cos}\:^{\mathrm{2}} {x}−\mathrm{2sin}\:{x}−\mathrm{3}\right)\:=\:\mathrm{0} \\ $$$$\begin{cases}{\mathrm{sin}\:{x}\:=\:\mathrm{0}\:\rightarrow\:{x}_{\mathrm{1}} \:=\:\mathrm{0}}\\{\mathrm{4cos}^{\mathrm{2}} \:{x}\:−\mathrm{2sin}\:{x}−\mathrm{3}\:=\:\mathrm{0}}\end{cases} \\ $$$$\mathrm{4}−\mathrm{4sin}\:^{\mathrm{2}} {x}−\mathrm{2sin}\:{x}−\mathrm{3}\:=\:\mathrm{0} \\ $$$$\mathrm{4sin}\:^{\mathrm{2}} {x}+\mathrm{2sin}\:{x}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{sin}\:{x}\:=\:\frac{−\mathrm{2}\:\pm\:\sqrt{\mathrm{4}+\mathrm{16}}}{\mathrm{8}}\:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\begin{cases}{{x}_{\mathrm{2}} =\:\mathrm{18}°\:=\:\frac{\pi}{\mathrm{10}}}\\{{x}_{\mathrm{3}} =\:−\mathrm{54}°=\:−\frac{\mathrm{3}\pi}{\mathrm{10}}\:\multimap\lozenge\multimap}\end{cases} \\ $$

Answered by Dwaipayan Shikari last updated on 24/Jul/20

2sinx(2cos^2 x−sinx)=3sinx 2−2sin^2 x−sinx=(3/2) or sinx=0 2sin^2 x+sinx−(1/2)=0 4sin^2 x+2sinx−1=0 sinx=((−2+(√(4+16)))/8)=((−(√5)±1)/4) or sinx=0 ⇒x=kπ sinx=sin(π/(10)) ( k∈Z) x=kπ±(π/(10)) or sinx=−((((√5)+1)/4)) x=−((3π)/(10)) Solutions are {(π/(10)),0,−((3π)/(10))}

$$\mathrm{2}{sinx}\left(\mathrm{2}{cos}^{\mathrm{2}} {x}−{sinx}\right)=\mathrm{3}{sinx} \\ $$$$\mathrm{2}−\mathrm{2}{sin}^{\mathrm{2}} {x}−{sinx}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:{or}\:\:{sinx}=\mathrm{0} \\ $$$$\mathrm{2}{sin}^{\mathrm{2}} {x}+{sinx}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{4}{sin}^{\mathrm{2}} {x}+\mathrm{2}{sinx}−\mathrm{1}=\mathrm{0} \\ $$$${sinx}=\frac{−\mathrm{2}+\sqrt{\mathrm{4}+\mathrm{16}}}{\mathrm{8}}=\frac{−\sqrt{\mathrm{5}}\pm\mathrm{1}}{\mathrm{4}}\:\:\:{or}\:{sinx}=\mathrm{0}\:\:\Rightarrow{x}={k}\pi \\ $$$${sinx}={sin}\frac{\pi}{\mathrm{10}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\:\:{k}\in\mathbb{Z}\right) \\ $$$${x}={k}\pi\pm\frac{\pi}{\mathrm{10}} \\ $$$${or}\:{sinx}=−\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right)\:\:\:{x}=−\frac{\mathrm{3}\pi}{\mathrm{10}} \\ $$$${Solutions}\:{are}\:\left\{\frac{\pi}{\mathrm{10}},\mathrm{0},−\frac{\mathrm{3}\pi}{\mathrm{10}}\right\} \\ $$

Answered by 1549442205PVT last updated on 24/Jul/20

⇔sinx(4cos^(2 ) x−2sinx−3)=0 ⇔sinx[(4(1−sin^(2 ) x)−2sinx−3]=0 ⇔sinx(4sin^2 x+2sinx−1)=0 i)sinx=0⇔x=kπ .Since x∈[−(π/2),(π/2)] ⇒x=0 ii)4sin^2 x+2sinx−1=0 ⇔sinx =((−1+(√5))/4) or sinx=((−1−(√5))/4) a)sinx=(((√5)−1)/4)=sin(π/(10))⇒x=(π/(10)) b)sinx=((−((√5)+1))/4)=sin((−3π)/(10))⇒x=((−3π)/(10)) Thus,x∈{0,(π/(10)),((−3π)/(10))}

$$\Leftrightarrow\mathrm{sinx}\left(\mathrm{4cos}^{\mathrm{2}\:} \mathrm{x}−\mathrm{2sinx}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{sinx}\left[\left(\mathrm{4}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}\:} \mathrm{x}\right)−\mathrm{2sinx}−\mathrm{3}\right]=\mathrm{0}\right. \\ $$$$\Leftrightarrow\mathrm{sinx}\left(\mathrm{4sin}^{\mathrm{2}} \mathrm{x}+\mathrm{2sinx}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left.\mathrm{i}\right)\mathrm{sinx}=\mathrm{0}\Leftrightarrow\mathrm{x}=\mathrm{k}\pi\:.\mathrm{Since}\:\mathrm{x}\in\left[−\frac{\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right] \\ $$$$\Rightarrow\mathrm{x}=\mathrm{0} \\ $$$$\left.\mathrm{ii}\right)\mathrm{4sin}^{\mathrm{2}} \mathrm{x}+\mathrm{2sinx}−\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{sinx}\:=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\:\mathrm{or}\:\mathrm{sinx}=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\left.\mathrm{a}\right)\mathrm{sinx}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}=\mathrm{sin}\frac{\pi}{\mathrm{10}}\Rightarrow\mathrm{x}=\frac{\pi}{\mathrm{10}} \\ $$$$\left.\mathrm{b}\right)\mathrm{sinx}=\frac{−\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{4}}=\mathrm{sin}\frac{−\mathrm{3}\pi}{\mathrm{10}}\Rightarrow\mathrm{x}=\frac{−\mathrm{3}\pi}{\mathrm{10}} \\ $$$$\mathrm{Thus},\mathrm{x}\in\left\{\mathrm{0},\frac{\pi}{\mathrm{10}},\frac{−\mathrm{3}\pi}{\mathrm{10}}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com